Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-19T17:40:47.167Z Has data issue: false hasContentIssue false
  • English
  • Français

NEW RESULTS ON SUM-PRODUCT TYPE GROWTH OVER FIELDS

Part of: Sequences and sets

Published online by Cambridge University Press:  02 April 2019

Brendan Murphy ,
Giorgis Petridis ,
Oliver Roche-Newton ,
Misha Rudnev  and
Ilya D. Shkredov
Brendan Murphy
Affiliation:
University of Bristol, Heilbronn Institute of Mathematical Research, School of Mathematics, University Walk, Bristol BS8 1TW, U.K. email brendan.murphy@bristol.ac.uk
Giorgis Petridis
Affiliation:
Department of Mathematics, University of Georgia, Athens, GA, 30602, U.S.A. email giogis@cantab.net
Oliver Roche-Newton
Affiliation:
Johann Radon Institute for Computational and Applied Mathematics (RICAM), 69 Altenberger Straße, 4040 Linz, Austria email o.rochenewton@gmail.com
Misha Rudnev
Affiliation:
University of Bristol, School of Mathematics, University Walk, Bristol BS8 1TW, U.K. email m.rudnev@bristol.ac.uk
Ilya D. Shkredov
Affiliation:
Steklov Mathematical Institute, ul. Gubkina, 8, Moscow, 119991, Russia IITP RAS, Bolshoy Karetny per. 19, Moscow, 127994, Russia MIPT, Institutskii per. 9, Dolgoprudnii, 141701, Russia email ilya.shkredov@gmail.com
Get access

Abstract

We prove a range of new sum-product type growth estimates over a general field 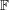$\mathbb{F}$, in particular the special case 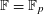$\mathbb{F}=\mathbb{F}_{p}$. They are unified by the theme of “breaking the 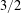$3/2$ threshold”, epitomizing the previous state of the art. This concerns two questions pivotal for the sum-product theory, which are lower bounds for the number of distinct cross-ratios determined by a finite subset of 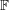$\mathbb{F}$, as well as the number of values of the symplectic form determined by a finite subset of 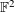$\mathbb{F}^{2}$. We establish the estimate 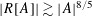$|R[A]|\gtrsim |A|^{8/5}$ for cardinality of the set 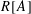$R[A]$ of distinct cross-ratios, defined by triples of elements of a set 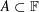$A\subset \mathbb{F}$ (sufficiently small if 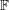$\mathbb{F}$ has positive characteristic, similarly for the rest of the estimates), pinned at infinity. The cross-ratio bound enables us to break the threshold in the second question: for a non-collinear point set 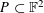$P\subset \mathbb{F}^{2}$, the number of distinct values of the symplectic form 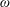$\unicode[STIX]{x1D714}$ on pairs of distinct points 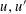$u,u^{\prime }$ of 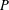$P$ is 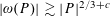$|\unicode[STIX]{x1D714}(P)|\gtrsim |P|^{2/3+c}$, with an explicit $c$. Symmetries of the cross-ratio underlie its local growth properties under both addition and multiplication, yielding an onset of growth of products of difference sets, which is another main result herein. Our proofs make use of specially suited applications of new incidence bounds over 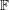$\mathbb{F}$, which apply to higher moments of representation functions. The technical thrust of the paper uses additive combinatorics to relate and adapt these higher moment bounds to growth estimates. A particular instance of this is breaking the threshold in the few sums, many products question over any 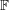$\mathbb{F}$, by showing that if 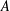$A$ is sufficiently small and has additive doubling constant 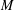$M$, then 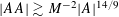$|AA|\gtrsim M^{-2}|A|^{14/9}$. This result has a second moment version, which allows for new upper bounds for the number of collinear point triples in the set 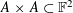$A\times A\subset \mathbb{F}^{2}$, the quantity often arising in applications of geometric incidence estimates.

MSC classification

Primary: 11B30: Arithmetic combinatorics; higher degree uniformity
Type
Research Article
Information
Mathematika , Volume 65 , Issue 3 , 2019 , pp. 588 - 642
Copyright
Copyright © University College London 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The second author was supported by the NSF DMS Award 1723016, by the RTG in Algebraic Geometry, Algebra, and Number Theory at the University of Georgia, and by the NSF RTG grant DMS-1344994. The third author was supported by the Austrian Science Fund FWF Project F5511-N26, which is part of the Special Research Program “Quasi-Monte Carlo Methods: Theory and Applications” as well as by the Austrian Science Fund FWF Project P 30405-N32.

References

Aksoy Yazici, E., Murphy, B., Rudnev, M. and Shkredov, I. D., Growth estimates in positive characteristic via collisions. Int. Math. Res. Not. IMRN 2017(23) 2017, 7148–7189.Google Scholar
Balog, A., Another sum-product estimate in finite fields. Proc. Steklov Inst. Math. 280(2) 2013, 23–29.Google Scholar
Balog, A., Roche-Newton, O. and Zhelezov, D., Expanders with superquadratic growth. Electron. J. Combin. 24(3) 2017, #P3.14.Google Scholar
Barak, B., Impagliazzo, R. and Wigderson, A., Extracting randomness using few independent sources. SIAM J. Comput. 36(4) 2006, 1095–1118.Google Scholar
Bennett, M., Hart, D., Iosevich, A., Pakianathan, J. and Rudnev, M., Group actions and geometric combinatorics in F q d . Forum Math. 29(1) 2017, 91–110.Google Scholar
Bourgain, J. and Chang, M.-C., On the size of k-fold sum and product sets of integers. J. Amer. Math. Soc. 17(2) 2004, 473–497 (electronic).Google Scholar
Bourgain, J., Glibichuk, A. A. and Konyagin, S. V., Estimates for the number of sums and products and for exponential sums in fields of prime order. J. Lond. Math. Soc. (2) 73 2006, 380–398.Google Scholar
Bourgain, J., Katz, N. H. and Tao, T., A sum-product estimate in finite fields, and applications. Geom. Funct. Anal. 14(1) 2004, 27–57.Google Scholar
Elekes, G. and Ruzsa, I. Z., Few sums, many products. Studia Sci. Math. Hungar. 40(3) 2003, 301–308.Google Scholar
Erdős, P. and Szemerédi, E., On sums and products of integers. In Studies in Pure Mathematics, Birkhäuser (Basel, 1983), 213–218.Google Scholar
Ford, K., The distribution of integers with a divisor in a given interval. Ann. of Math. (2) 168(2) 2008, 367–433.Google Scholar
Garaev, M. Z. and Shen, C.-Y., On the size of the set A (A + 1). Math. Z. 265(1) 2010, 125–132.Google Scholar
Guth, L. and Katz, N. H., On the Erdős distinct distances problem in the plane. Ann. of Math. (2) 181(1) 2015, 155–190.Google Scholar
Hart, D., Iosevich, A. and Solymosi, J., Sum-product estimates in finite fields via Kloosterman sums. Int. Math. Res. Not. IMRN 2007 2007,rnm007.Google Scholar
Heath-Brown, D. R. and Konyagin, S. V., New bounds for Gauss sums derived from kth powers, and for Heilbronn’s exponential sum. Q. J. Math. 51(2) 2000, 221–235.Google Scholar
Helfgott, H. A., Growth in groups: ideas and perspectives. Bull. Amer. Math. Soc. 52(3) 2015, 357–413.Google Scholar
Iosevich, A., Roche-Newton, O. and Rudnev, M., On an application of Guth–Katz theorem. Math. Res. Lett. 18(4) 2011, 691–697.Google Scholar
Iosevich, A., Roche-Newton, O. and Rudnev, M., On discrete values of bilinear forms. Mat. Sb. 209(10) 2018, 71–88.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, American Mathematical Society (Providence, RI, 2004).Google Scholar
Jones, T. G. F., New quantitative estimates on the incidence geometry and growth of finite sets. PhD Thesis, University of Bristol, 2013.Google Scholar
Katz, N. H. and Shen, C.-Y., A slight improvement to Garaev’s sum product estimate. Proc. Amer. Math. Soc. 136(7) 2008, 2499–2504.Google Scholar
Konyagin, S. V., A sum-product estimate in fields of prime order. Preprint, 2003,arXiv:math/0304217.Google Scholar
Konyagin, S. V. and Rudnev, M., On new sum-product type estimates. SIAM J. Discrete Math. 27(2) 2013, 973–990.Google Scholar
Macourt, S., Shparlinski, I. E. and Shkredov, I. D., Multiplicative energy of shifted subgroups and bounds on exponential sums with trinomials in finite fields. Canad. J. Math. 70(6) 2018, 1319–1338.Google Scholar
Murphy, B. and Petridis, G., A point-line incidence identity in finite fields, and applications. Mosc. J. Comb. Number Theory 6(1) 2016, 63–94.Google Scholar
Murphy, B. and Petridis, G., A second wave of expanders over finite fields. In Combinatorial and Additive Number Theory II: CANT 2015 and 2016, (ed. Nathanson, M. B.), Springer (Cham, 2017), 215–238.Google Scholar
Petridis, G., New proofs of Plunnecke-type estimates for product sets in groups. Combinatorica 32(6) 2012, 721–733.Google Scholar
Petridis, G., Products of differences in prime order finite fields. Preprint, 2016, arXiv:1602.02142.Google Scholar
Petridis, G. and Shparlinski, I. E., Bounds on trilinear and quadrilinear exponential sums. J. Anal. Math. (to appear). Preprint, 2016, arXiv:1604.08469.Google Scholar
Pham, T., Vinh, L. A. and de Zeeuw, F., Three-variable expanding polynomials and higher-dimensional distinct distances. Combinatorica (to appear).Google Scholar
Roche-Newton, O., A short proof of a near-optimal cardinality estimate for the product of a sum set. In 31st International Symposium on Computational Geometry (SoCG 2015) (Leibniz International Proceedings in Informatics 34 ) (eds Arge, L. and Pach, J.), Dagstuhl Publishing (2015), 74–80.Google Scholar
Roche-Newton, O., Rudnev, M. and Shkredov, I. D., New sum-product type estimates over finite fields. Adv. Math. 293 2016, 589–605.Google Scholar
Roche-Newton, O. and Zhelezov, D., A bound on the multiplicative energy of a sum set and extremal sum-product problems. Mosc. J. Comb. Number Theory 5(1–2) 2015, 52–69.Google Scholar
Rudnev, M., On distinct cross-ratios and related growth problems. Mosc. J. Comb. Number Theory 7(3) 2017, 237–251.Google Scholar
Rudnev, M., On the number of incidences between planes and points in three dimensions. Combinatorica 38(1) 2018, 219–254.Google Scholar
Rudnev, M., Shakan, G. and Skredov, I. D., Stronger sum-product inequalities for small sets. Preprint, 2018, arXiv:1808.08465.Google Scholar
Rudnev, M., Shkredov, I. D. and Stevens, S., On the energy variant of the sum-product conjecture. Rev. Mat. Iberoam. (accepted). Preprint, 2016, arXiv:1607.05053.Google Scholar
Schoen, T. and Shkredov, I. D., On sumsets of convex sets. Combin. Probab. Comput. 20 2011, 793–798.Google Scholar
Schoen, T. and Shkredov, I. D., Higher moments of convolutions. J. Number Theory 133 2013, 1693–1737.Google Scholar
Semple, J. G. and Kneebone, G. T., Algebraic Projective Geometry, Clarendon Press (Oxford, 1956).Google Scholar
Shakan, G., On higher energy decompositions and the sum-product phenomenon. Math. Proc. Camb. Philos. Soc. 2018, doi:10.1017/S0305004118000506.Google Scholar
Shkredov, I. D., Some new results on higher energies. Trans. Moscow Math. Soc. 74 2013, 31–63.Google Scholar
Shkredov, I. D., On sums of Szemerédi–Trotter sets. Trans. Steklov Math. Inst. 289 2015, 300–309.Google Scholar
Shkredov, I. D., Difference sets are not multiplicatively closed. Discrete Anal. 17 2016, 1–21.Google Scholar
Shkredov, I. D., Some remarks on sets with small quotient set. Sb. Math. 208(12) 2016, 144–158.Google Scholar
Shkredov, I. D., Any small multiplicative sugroup is not a sumset. Preprint, 2017, arXiv:1702.01197.Google Scholar
Shkredov, I. D. and Vyugin, I. V., On additive shifts of multiplicative subgroups. Mat. Sb. 203(6) 2012, 81–100.Google Scholar
Shkredov, I. D. and Zhelezov, D., On additive bases of sets with small product set. Int. Math. Res. Not. IMRN 2018(5) 2018, 1585–1599.Google Scholar
Shparlinski, I. E., Additive decompositions of subgroups of finite fields. SIAM J. Discrete Math. 27(6) 2013, 1870–1879.Google Scholar
Solymosi, J., On the number of sums and products. Bull. Lond. Math. Soc. 37(4) 2005, 491–494.Google Scholar
Solymosi, J., Bounding multiplicative energy by the sumset. Adv. Math. 222(2) 2009, 402–408.Google Scholar
Stevens, S. and de Zeeuw, F., An improved point-line incidence bound over arbitrary fields. Bull. Lond. Math. Soc. 49(5) 2016, 842–858.Google Scholar
Szemerédi, E. and Trotter, W. T., Extremal problems in discrete geometry. Combinatorica 3(3–4) 1983, 381–392.Google Scholar
Szőnyi, T., Around Rédei’s theorem. Discrete Math. 208/209 1999, 557–575.Google Scholar
Tóth, C. D., The Szemerédi–Trotter theorem in the complex plane. Combinatorica 35(1) 2015, 95–126.Google Scholar
Vinh, L. A., The Szemerédi–Trotter type theorem and the sum-product estimate in finite fields. European J. Combin. 32(8) 2011, 1177–1181.Google Scholar
Zuckerman, D., General weak random sources. In 31st Annual Symposium on Foundations of Computer Science, Vols I, II (St. Louis, MO, 1990), IEEE Computer Society Press (Los Alamitos, CA, 1990), 534–543.Google Scholar
Zuckerman, D., Simulating BPP using a general weak random source. In 32nd Annual Symposium on Foundations of Computer Science (San Juan, PR, 1991), IEEE Computer Society Press (Los Alamitos, CA, 1991), 79–89.Google Scholar