Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-25T00:14:41.204Z Has data issue: false hasContentIssue false
  • English
  • Français

ITERATION OF QUADRATIC POLYNOMIALS OVER FINITE FIELDS

Part of: Computational number theory Finite fields and commutative rings (number-theoretic aspects) Arithmetic algebraic geometry Arithmetic and non-Archimedean dynamical systems Polynomials and matrices

Published online by Cambridge University Press:  29 November 2017

D. R. Heath-Brown
D. R. Heath-Brown*
Affiliation:
Mathematical Institute, Radcliffe Observatory Quarter, Woodstock Road, Oxford, OX2 6GG, U.K. email rhb@maths.ox.ac.uk
Get access

Abstract

For a finite field of odd cardinality 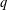$q$, we show that the sequence of iterates of 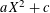$aX^{2}+c$, starting at 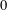$0$, always recurs after 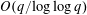$O(q/\text{log}\log q)$ steps. For 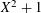$X^{2}+1$, the same is true for any starting value. We suggest that the traditional “birthday paradox” model is inappropriate for iterates of 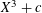$X^{3}+c$, when 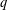$q$ is 2 mod 3.

MSC classification

Primary: 11T06: Polynomials
Secondary: 11C08: Polynomials 11G20: Curves over finite and local fields 11Y05: Factorization 37P05: Polynomial and rational maps 37P25: Finite ground fields
Type
Research Article
Information
Mathematika , Volume 63 , Issue 3 , 2017 , pp. 1041 - 1059
Copyright
Copyright © University College London 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Browning, T. D. and Heath-Brown, D. R., Forms in many variables and differing degrees. J. Eur. Math. Soc. (JEMS) 19 2017, 357–394.CrossRefGoogle Scholar
Castelnuovo, G., Ricerche di geometria sulle curve algebriche. Atti Reale Accad. Sci. Torino 24 1889, 346–373.Google Scholar
Juul, J., Kurlberg, P., Madhu, K. and Tucker, T. J., Wreath products and proportions of periodic points. Int. Math. Res. Not. IMRN 2016(13) 2016, 3944–3969.Google Scholar
Pollard, J. M., A Monte Carlo method for factorization. Nordisk Tidskr. Informationsbehandling (BIT) 15(3) 1975, 331–334.Google Scholar
Shao, X., Polynomial values modulo primes on average and sharpness of the larger sieve. Algebra Number Theory 9(10) 2015, 2325–2346.Google Scholar