Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-23T10:10:17.326Z Has data issue: false hasContentIssue false
  • English
  • Français

ILLUMINATION OF CONVEX BODIES WITH MANY SYMMETRIES

Part of: Discrete geometry General convexity

Published online by Cambridge University Press:  16 February 2017

Konstantin Tikhomirov
Konstantin Tikhomirov*
Affiliation:
Department of Mathematical and Statistical Sciences, University of Alberta, CAB 632, Edmonton AB T6G 2G1, Canada email ktikhomi@ualberta.ca, kt12@math.princeton.edu Department of Mathematics, Princeton University, Princeton NJ 08544, U.S.A.
Get access

Abstract

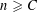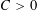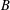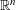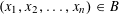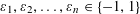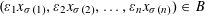Let $n\geqslant C$ for a large universal constant $C>0$ and let $B$ be a convex body in $\mathbb{R}^{n}$ such that for any $(x_{1},x_{2},\ldots ,x_{n})\in B$, any choice of signs $\unicode[STIX]{x1D700}_{1},\unicode[STIX]{x1D700}_{2},\ldots ,\unicode[STIX]{x1D700}_{n}\in \{-1,1\}$ and for any permutation $\unicode[STIX]{x1D70E}$ on $n$ elements, we have $(\unicode[STIX]{x1D700}_{1}x_{\unicode[STIX]{x1D70E}(1)},\unicode[STIX]{x1D700}_{2}x_{\unicode[STIX]{x1D70E}(2)},\ldots ,\unicode[STIX]{x1D700}_{n}x_{\unicode[STIX]{x1D70E}(n)})\in B$. We show that if 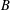$B$ is not a cube, then 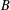$B$ can be illuminated by strictly less than 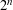$2^{n}$ sources of light. This confirms the Hadwiger–Gohberg–Markus illumination conjecture for unit balls of 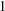$1$-symmetric norms in 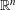$\mathbb{R}^{n}$ for all sufficiently large $n$.

MSC classification

Primary: 52A20: Convex sets in $n$ dimensions (including convex hypersurfaces) 52C17: Packing and covering in $n$ dimensions
Type
Research Article
Information
Mathematika , Volume 63 , Issue 2 , 2017 , pp. 372 - 382
Copyright
Copyright © University College London 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bezdek, K., Classical Topics in Discrete Geometry (CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC), Springer (New York, 2010); MR 2664371.Google Scholar
Bezdek, K., Illuminating spindle convex bodies and minimizing the volume of spherical sets of constant width. Discrete Comput. Geom. 47(2) 2012, 275–287; MR 2872538.CrossRefGoogle Scholar
Bezdek, K. and Bisztriczky, T., A proof of Hadwiger’s covering conjecture for dual cyclic polytopes. Geom. Dedicata 68(1) 1997, 29–41; MR 1485381.Google Scholar
Bezdek, K. and Khan, M. A., The geometry of homothetic covering and illumination. Preprint, 2016, arXiv:1602.06040.Google Scholar
Boltyanskiĭ, V. G., Solution of the illumination problem for belt-bodies. Mat. Zametki 58(4) 1995, 505–511 (in Russian); English translation in Math. Notes 58(4) (1995), 1029–1032; MR 1378331.Google Scholar
Boltyanski, V., Martini, H. and Soltan, P. S., Excursions into Combinatorial Geometry (Universitext), Springer (Berlin, 1997); MR 1439963.Google Scholar
Hadwiger, H., Ungelöste Probleme. Elem. Math. 12(20) 1957, 121.Google Scholar
Hadwiger, H., Ungelöste Probleme. Elem. Math. 15(38) 1960, 130–131.Google Scholar
Livshyts, G. and Tikhomirov, K., Randomized coverings of a convex body with its homothetic copies, and illumination. Preprint, 2016, arXiv:1606.08876.Google Scholar
Martini, H., Some results and problems around zonotopes. In Intuitive Geometry (Siófok, 1985) (Colloq. Math. Soc. János Bolyai 48 ), North-Holland (Amsterdam), 383–418; MR 0910725.Google Scholar
Naszódi, M., A spiky ball. Mathematika 62(2) 2016, 630–636; MR 3521345.Google Scholar
Rogers, C. A., A note on coverings. Mathematika 4 1957, 1–6; MR 0090824.Google Scholar
Schramm, O., Illuminating sets of constant width. Mathematika 35(2) 1988, 180–189;MR 0986627.CrossRefGoogle Scholar