Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-26T18:12:41.785Z Has data issue: false hasContentIssue false
  • English
  • Français

The Hausdorff dimension of systems of simultaneously small linear forms

Part of: Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  26 February 2010

H. Dickinson
H. Dickinson
Affiliation:
Department of Mathematics, The University of YorkHeslington, York, YO1 5DD
Get access

Extract

In this paper the Hausdorff dimension of systems of real linear forms which are simultaneously small for infinitely many integer vectors is determined. A system of real linear forms,

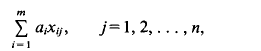
where ai, xij∈ℝ, 1 ≤i≤m, 1≤j≤n will be denoted more concisely as

where a∈⇝m, X∈ℝmn and ℝmn is identified with Mm × n(ℝ), the set of real m × n matrices. The supremum norm 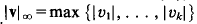of any vector in k dimensional Euclidean space, ℝk will be denoted by |v|. The distance of a point a from a set B, will be denoted by dist (a, B) = inf {|a − b|: b ∈ B}.

MSC classification

Secondary: 11J13: Simultaneous homogeneous approximation, linear forms
Type
Research Article
Information
Mathematika , Volume 40 , Issue 2 , December 1993 , pp. 367 - 374
Copyright
Copyright © University College London 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bovey, J. D. and Dodson, M. M.. The fractional dimension of sets whose simultaneous rational approximation have errors with a small product. Bull. London Math. Soc., 10 (1978), 213–218.CrossRefGoogle Scholar
2.Bovey, J. D. and Dodson, M. M.. The Hausdorff dimension of systems of linear forms. Ada Arith., 10 (1986), pp. 337–358.CrossRefGoogle Scholar
3.Cassels, J. W. S.. An introduction to Diophantine approximation (Cambridge University Press, 1957).Google Scholar
4.Dodson, M. M., Rynne, B. P. and Vickers, J. A. G.. Diophantine approximation and a lower bound for Hausdorff dimension. Mathematika, 37 (1990), 59–73.CrossRefGoogle Scholar
5.Dodson, M. M. and Vickers, J. A. G.. Exceptional sets in Kolmogorov-Arnol'd-Moser theory. J. Phys. A: Math. Gen., 19 (1986), 349–374.CrossRefGoogle Scholar
6.Falconer, K. J.. The geometry of fractal sets (Cambridge University Press, 1985).CrossRefGoogle Scholar
6.Falconer, K. J.. Classes of sets with large intersection. Mathematika, 32 (1985), 191–205.CrossRefGoogle Scholar
8.Guillemin, V. and Pollack, A.. Differential topology (Prentice Hall International, 1974).Google Scholar
9.Larman, D. G.. On Hausdorff measure in finite dimensional compact metric spaces. Proc. London Math. Soc. (3), 17 (1967), 193–206.CrossRefGoogle Scholar