Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
  • Home
Hostname: page-component-78dcdb465f-vddjc Total loading time: 0.871 Render date: 2021-04-17T13:05:46.849Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "metricsAbstractViews": false, "figures": false, "newCiteModal": false, "newCitedByModal": true }
EnglishFrançais
Mathematika Mathematika

Article contents

EXPLICIT BOUNDS ON AUTOMORPHIC AND CANONICAL GREEN FUNCTIONS OF FUCHSIAN GROUPS

Part of: Discontinuous groups and automorphic forms Arithmetic problems. Diophantine geometry Riemann surfaces Elliptic equations and systems

Published online by Cambridge University Press:  14 May 2014

Peter Bruin
Peter Bruin
Affiliation:
Mathematics Institute, Zeeman Building,University of Warwick, Coventry CV4 7AL,U.K. email P.Bruin@warwick.ac.uk
Corresponding
E-mail address:
P.Bruin@warwick.ac.uk
Get access
Rights & Permissions[Opens in a new window]

Abstract

We study the automorphic Green function 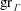$\mathop{\rm gr}\nolimits _\Gamma $ on quotients of the hyperbolic plane by cofinite Fuchsian groups 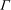$\Gamma $, and the canonical Green function 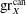$\mathop{\rm gr}\nolimits ^{\rm can}_X$ on the standard compactification 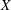$X$ of such a quotient. We use a limiting procedure, starting from the resolvent kernel, and lattice point estimates for the action of 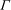$\Gamma $ on the hyperbolic plane to prove an “approximate spectral representation” for 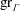$\mathop{\rm gr}\nolimits _\Gamma $. Combining this with bounds on Maaß forms and Eisenstein series for 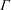$\Gamma $, we prove explicit bounds on 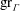$\mathop{\rm gr}\nolimits _\Gamma $. From these results on 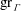$\mathop{\rm gr}\nolimits _\Gamma $ and new explicit bounds on the canonical 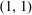$(1,1)$-form of 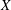$X$, we deduce explicit bounds on 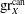$\mathop{\rm gr}\nolimits ^{\rm can}_X$.

MSC classification

Secondary: 11F72: Spectral theory; Selberg trace formula 30F35: Fuchsian groups and automorphic functions 35J08: Green's functions 14G35: Modular and Shimura varieties 14G40: Arithmetic varieties and schemes; Arakelov theory; heights
Type
Research Article
Information
Mathematika , Volume 60 , Issue 2 , July 2014 , pp. 257 - 306
Copyright
Copyright © University College London 2014 

Access options

Get access to the full version of this content by using one of the access options below.
If you should have access and can't see this content please contact technical support.

References

Араҡелов, С. Ю., Теория пересечений дивизоров на арифметичесҡой поверхности. Известия Аҡадемии Науҡ CCCP 38(6) 1974, 1179–1192 ; S. Yu. Arakelov, Intersection theory of divisors on an arithmetic surface. Math. USSR Izv. 8 (1974), 1167–1180 (Engl. transl.).Google Scholar
Aryasomayajula, A., Bounds for Green’s functions on hyperbolic Riemann surfaces of finite volume. Dissertation, Humboldt-Universität zu Berlin, 2013.Google Scholar
Bruin, P. J., Modular curves, Arakelov theory, algorithmic applications. Proefschrift (PhD Thesis), Universiteit Leiden, 2010.Google Scholar
Delsarte, J., Sur le gitter fuchsien. C. R. Acad. Sci. Paris 214 1942, 147–179.Google Scholar
Edixhoven, S. J., Couveignes, J.-M., de Jong, R. S., Merkl, F. and Bosman, J. G., Computational Aspects of Modular Forms and Galois Representations (Annals of Mathematics Studies 176), Princeton University Press (2011).CrossRefGoogle Scholar
Elkik, R., Fonctions de Green, volumes de Faltings, application aux surfaces arithmétiques. Exposé III dans : L. Szpiro. In Séminaire sur les pinceaux arithmétiques : la conjecture de Mordell (Astérisque 127), Société Mathematique de France (1985), 89–112.Google Scholar
Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G., Higher Transcendental Functions, Volume I (Bateman Manuscript Project, California Institute of Technology), McGraw-Hill (1953).Google Scholar
Фаддеев, Л. Д., Разложение по собственным фунҡциям оператора Лапласа на фундаментальной области дисҡретной группы на плосҡости Лобачевсҡого. Труды Мосҡовсҡого Математичесҡого Общества 17 1966, 323–350 ; L. D. Faddeev, Expansion in eigenfunctions of the Laplace operator on the fundamental domain of a discrete group on the Lobačevskiĭ plane. Trans. Moscow Math. Soc. 17 (1967), 357–386 (Engl. transl.).Google Scholar
Faltings, G., Calculus on arithmetic surfaces. Ann. of Math. (2) 119 1984, 387–424.CrossRefGoogle Scholar
Fay, J. D., Fourier coefficients of the resolvent for a Fuchsian group. J. Reine Angew. Math. 293/294 1977, 143–203.Google Scholar
Hejhal, D. A., The Selberg Trace Formula for  PSL(2, R), Vol. 2 (Lecture Notes in Mathematics 1001), Springer (1983).CrossRefGoogle Scholar
Huber, H., Über eine neue Klasse automorpher Funktionen und ein Gitterpunktproblem in der hyperbolischen Ebene. I. Comment. Math. Helv. 30 1956, 20–62.CrossRefGoogle Scholar
Iwaniec, H., Introduction to the Spectral Theory of Automorphic Forms, Revista Matemática Iberoamericana (Madrid, 1995).Google Scholar
Jorgenson, J. and Kramer, J., Bounding the sup-norm of automorphic forms. Geom. Funct. Anal. 14(6) 2005, 1267–1277.CrossRefGoogle Scholar
Jorgenson, J. and Kramer, J., Bounds on canonical Green’s functions. Compositio Math. 142(3) 2006, 679–700.CrossRefGoogle Scholar
Kim, H. H., Functoriality for the exterior square of GL4and the symmetric fourth of GL2. With appendix 1 by D. Ramakrishnan and appendix 2 by Kim and P. Sarnak. J. Amer. Math. Soc. 16(1) 2003, 139–183.CrossRefGoogle Scholar
Maaß, H., Über eine neue Art von nichtanalytischen automorphen Funktionen und die Bestimmung Dirichletscher Reihen durch Funktionalgleichungen. Math. Ann. 121 1949, 141–183.CrossRefGoogle Scholar
The PARI Group, pari/gp computer algebra system, version 2.5.1. Bordeaux, 2011,http://pari.math.u-bordeaux.fr/.Google Scholar
Patterson, S. J., A lattice problem in hyperbolic space. Mathematika 22 1975, 81–88.CrossRefGoogle Scholar
Selberg, A., Harmonic analysis and discontinuous groups in weakly symmetric Riemannian spaces with applications to Dirichlet series. J. Indian Math. Soc. (N.S.) 20 1956, 47–87 ($=$Collected Papers 1, Springer (Berlin, 1989), 423–463).Google Scholar
Selberg, A., Discontinuous groups and harmonic analysis. In Proceedings of the International Congress of Mathematicians (Stockholm, 15–22 August, 1962), Institut Mittag-Leffler (Djursholm, 1963), 177–189 (= Collected Papers 1, Springer (Berlin, 1989), 493–505).Google Scholar
Selberg, A., On the estimation of Fourier coefficients of modular forms. In Theory of Numbers (Proceedings of Symposia in Pure Mathematics VIII) (ed. Whiteman, A. L.), American Mathematical Society (Providence, RI, 1965), 1–15 ($=$ Collected Papers 1, Springer (Berlin, 1989), 506–520).Google Scholar

Full text views

Full text views reflects PDF downloads, PDFs sent to Google Drive, Dropbox and Kindle and HTML full text views.

Total number of HTML views: 0
Total number of PDF views: 32 *
View data table for this chart

* Views captured on Cambridge Core between September 2016 - 17th April 2021. This data will be updated every 24 hours.

3
Cited by

Send article to Kindle

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

EXPLICIT BOUNDS ON AUTOMORPHIC AND CANONICAL GREEN FUNCTIONS OF FUCHSIAN GROUPS
Available formats
×

Send article to Dropbox

To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.

EXPLICIT BOUNDS ON AUTOMORPHIC AND CANONICAL GREEN FUNCTIONS OF FUCHSIAN GROUPS
Available formats
×

Send article to Google Drive

To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.

EXPLICIT BOUNDS ON AUTOMORPHIC AND CANONICAL GREEN FUNCTIONS OF FUCHSIAN GROUPS
Available formats
×
×

Reply to: Submit a response

Your details

Conflicting interests

Do you have any conflicting interests? *