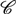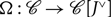Editorial Preface
A special issue on categorical algebras and computation in celebration of John Power’s 60th birthday, part I
-
- Published online by Cambridge University Press:
- 28 February 2022, pp. 746-747
-
- Article
-
- You have access
- Export citation
Paper
Freely adjoining monoidal duals
-
- Published online by Cambridge University Press:
- 28 October 2020, pp. 748-768
-
- Article
- Export citation
Doctrines, modalities and comonads
-
- Published online by Cambridge University Press:
- 14 September 2021, pp. 769-798
-
- Article
-
- You have access
- Open access
- Export citation
Finitary monads on the category of posets
-
- Published online by Cambridge University Press:
- 26 November 2021, pp. 799-821
-
- Article
-
- You have access
- Open access
- Export citation
Coherence for bicategorical cartesian closed structure
-
- Published online by Cambridge University Press:
- 18 October 2021, pp. 822-849
-
- Article
- Export citation