Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-26T04:20:25.100Z Has data issue: false hasContentIssue false
  • English
  • Français

Identity types and weak factorization systems in Cauchy complete categories

Published online by Cambridge University Press:  29 March 2019

Paige Randall North Open the ORCID record for Paige Randall North [Opens in a new window]
Paige Randall North*
Affiliation:
Department of Mathematics, the Ohio State University, 231 W 18th Ave, Columbus, OH 43210, USA
*
*Corresponding author. Email: north.138@osu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

It has been known that categorical interpretations of dependent type theory with Σ- and Id-types induce weak factorization systems. When one has a weak factorization system 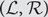$({\cal L},{\cal R})$ on a category 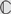$\mathbb{C}$ in hand, it is then natural to ask whether or not 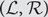$({\cal L},{\cal R})$ harbors an interpretation of dependent type theory with Σ- and Id- (and possibly Π-) types. Using the framework of display map categories to phrase this question more precisely, one would ask whether or not there exists a class 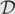${\cal D}$ of morphisms of 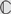$\mathbb{C}$ such that the retract closure of 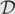${\cal D}$ is the class 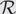${\cal R}$ and the pair 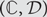$(\mathbb{C},{\cal D})$ forms a display map category modeling Σ- and Id- (and possibly Π-) types. In this paper, we show, with the hypothesis that 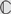$\cal{C}$ is Cauchy complete, that there exists such a class 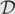$\cal{D}$ if and only if 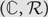$(\mathbb{C},\cal{R})$itself forms a display map category modeling Σ- and Id- (and possibly Π-) types. Thus, we reduce the search space of our original question from a potentially proper class to a singleton.

Keywords

Dependent type theoryidentity typesweak factorization systemsdisplay map categories
Type
Paper
Information
Mathematical Structures in Computer Science , Volume 29 , Issue 9 , October 2019 , pp. 1411 - 1427
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

This material is based upon work supported by the Air Force Office of Scientific Research under award number FA9550-16-1-0212.

References

Awodey, S. and Warren, M.A. (2009). Homotopy theoretic models of identity types. Mathematical Proceedings of the Cambridge Philosophical Society 146 (1) 45–55.CrossRefGoogle Scholar
Borceux, F. (1994). Handbook of Categorical Algebra, vol. 1. Cambridge, UK, Cambridge University Press.Google Scholar
Emmenegger, J. (2014) A Category-Theoretic Version of the Identity Type Weak Factorization System. arXiv:1412.0153 [math.LO].Google Scholar
Gambino, N. and Garner, R. (2008). The identity type weak factorisation system. Theoretical Computer Science 409 (1) 94–109.CrossRefGoogle Scholar
Hovey, M. (1999). Model Categories. Providence, RI, American Mathematical Society.Google Scholar
Joyal, A. (2017). Notes on Clans and Tribes. arXiv:1710.10238 [math.CT].Google Scholar
Lumsdaine, P.L. and Warren, M.A. (2015). The local universes model: an overlooked coherence construction for dependent type theories. ACM Transactions on Computational Logic 16 (3) Art. 23, 31.CrossRefGoogle Scholar
May, J.P. and Ponto, K. (2012). More Concise Algebraic Topology. Chicago, University of Chicago Press.Google Scholar
Moss, S. (2018). The Dialectica Models of Type Theory. PhD thesis, University of Cambridge.CrossRefGoogle Scholar
Nordström, B. Petersson, K. and Smith, J.M. (2000). Martin-Löf’s Type Theory. In: Handbook of Logic in Computer Science, Oxford, UK, Oxford University Press, 1–32.Google Scholar
North, P.R. (2017). Type Theoretic Weak Factorization Systems. PhD thesis, University of Cambridge.Google Scholar
Shulman, M. (2015) Univalence for inverse diagrams and homotopy canonicity. Mathematical Structures in Computer Science 25 (5) 1203–1277.CrossRefGoogle Scholar
Streicher, T. (1993). Investigations into Intensional Type Theory. Habilitationsschrift. Ludwig Maximilian University of Munich.Google Scholar
Taylor, P. (1999). Practical Foundations of Mathematics. Cambridge, UK, Cambridge University Press.Google Scholar
van den Berg, B. and Garner, R. (2012). Topological and simplicial models of identity types. ACM Transactions on Computational Logic 13 (1) 3:1–3:44.CrossRefGoogle Scholar
Warren, M.A. (2008). Homotopy Theoretic Aspects of Constructive Type Theory. Phd thesis, Carnegie Mellon University.Google Scholar