A subset Y of the general linear group
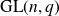 $\text{GL}(n,q)$
is called t-intersecting if
$\text{GL}(n,q)$
is called t-intersecting if
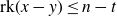 $\text{rk}(x-y)\le n-t$
for all
$\text{rk}(x-y)\le n-t$
for all
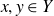 $x,y\in Y$
, or equivalently x and y agree pointwise on a t-dimensional subspace of
$x,y\in Y$
, or equivalently x and y agree pointwise on a t-dimensional subspace of
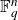 $\mathbb{F}_q^n$
for all
$\mathbb{F}_q^n$
for all
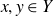 $x,y\in Y$
. We show that, if n is sufficiently large compared to t, the size of every such t-intersecting set is at most that of the stabiliser of a basis of a t-dimensional subspace of
$x,y\in Y$
. We show that, if n is sufficiently large compared to t, the size of every such t-intersecting set is at most that of the stabiliser of a basis of a t-dimensional subspace of
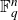 $\mathbb{F}_q^n$
. In case of equality, the characteristic vector of Y is a linear combination of the characteristic vectors of the cosets of these stabilisers. We also give similar results for subsets of
$\mathbb{F}_q^n$
. In case of equality, the characteristic vector of Y is a linear combination of the characteristic vectors of the cosets of these stabilisers. We also give similar results for subsets of
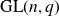 $\text{GL}(n,q)$
that intersect not necessarily pointwise in t-dimensional subspaces of
$\text{GL}(n,q)$
that intersect not necessarily pointwise in t-dimensional subspaces of
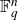 $\mathbb{F}_q^n$
and for cross-intersecting subsets of
$\mathbb{F}_q^n$
and for cross-intersecting subsets of
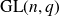 $\text{GL}(n,q)$
. These results may be viewed as variants of the classical Erdős–Ko–Rado Theorem in extremal set theory and are q-analogs of corresponding results known for the symmetric group. Our methods are based on eigenvalue techniques to estimate the size of the largest independent sets in graphs and crucially involve the representation theory of
$\text{GL}(n,q)$
. These results may be viewed as variants of the classical Erdős–Ko–Rado Theorem in extremal set theory and are q-analogs of corresponding results known for the symmetric group. Our methods are based on eigenvalue techniques to estimate the size of the largest independent sets in graphs and crucially involve the representation theory of
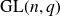 $\text{GL}(n,q)$
.
$\text{GL}(n,q)$
.