Article contents
Tb theorem on product spaces
Published online by Cambridge University Press: 28 March 2016
Abstract
In this paper, we prove a Tb theorem on product spaces 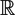 $\mathbb{R}$n ×
$\mathbb{R}$n × 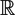 $\mathbb{R}$m, where b(x1, x2) = b1(x1)b2(x2), b1 and b2 are para-accretive functions on
$\mathbb{R}$m, where b(x1, x2) = b1(x1)b2(x2), b1 and b2 are para-accretive functions on 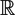 $\mathbb{R}$n and
$\mathbb{R}$n and 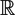 $\mathbb{R}$m, respectively.
$\mathbb{R}$m, respectively.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 161 , Issue 1 , July 2016 , pp. 117 - 141
- Copyright
- Copyright © Cambridge Philosophical Society 2016
References
REFERENCES
- 1
- Cited by




