Hostname: page-component-84b7d79bbc-g5fl4 Total loading time: 0 Render date: 2024-07-25T13:59:15.344Z Has data issue: false hasContentIssue false
  • English
  • Français

Singular infinitely divisible distributions whose characteristic functions vanish at infinity

Published online by Cambridge University Press:  24 October 2008

Gavin Brown
Gavin Brown
Affiliation:
University of New South Wales
Get access Rights & Permissions [Opens in a new window]

Extract

In the course of discussing dynamical systems which enjoy strong mixing but have singular spectrum, E. Hewitt and the author, (2), recently constructed families 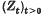of symmetric random variables which satisfy inter alia the following properties:

(i) Zt is purely singular and has full support,

(ii) χ(t)(x) → 0 as ± x → ∞, where χ(t) is the characteristic function of Zt,

(iii)′ Zt+s, Zt + Zs have the same null events,

(iv) whenever s ≠ t, Zt and Zs + a are mutually singular for every (possibly zero) constant a.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 82 , Issue 2 , September 1977 , pp. 277 - 287
Copyright
Copyright © Cambridge Philosophical Society 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Brown, G.M 0(G) has a symmetric maximal ideal off the Šilov boundary. Proc. London Math. Soc. (3) 27 (1973), 484–504.CrossRefGoogle Scholar
(2)Brown, G. and Hewitt, E.Continuous singular measures equivalent to their convolution squares. Math. Proc. Cambridge Philos. Soc. 80 (1976), 249–268.CrossRefGoogle Scholar
(3)Brown, G. and Moran, W.A dichotomy for infinite convolutions of discrete measures. Proc. Cambridge Philos. Soc. 73 (1973), 307–316.CrossRefGoogle Scholar
(4)Brown, G. and Moran, W.Coin-tossing and powers of singular measures. Math. Proc. Cambridge Philos. Soc. 77 (1975), 349–364.CrossRefGoogle Scholar
(5)Peyrière, J.Sur les produits de Riesz. C.R. Acad. Sci. Paris Sér. A–B 276 (1973), 1453–1455.Google Scholar
(6)Tucker, H. G.On a necessary and sufficient condition that an infinitely divisible distribution be absolutely continuous. Trans. Amer. Math. Soc. 118 (1965), 316–330.CrossRefGoogle Scholar