Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-26T14:34:44.824Z Has data issue: false hasContentIssue false
  • English
  • Français

The representation theory of C*-algebras associated to groupoids

Published online by Cambridge University Press:  27 February 2012

LISA ORLOFF CLARK  and
ASTRID AN HUEF
LISA ORLOFF CLARK
Affiliation:
Department of Mathematics and Statistics, University of Otago, PO Box 56, Dunedin 9054, New Zealand. e-mail: lclark@maths.otago.ac.nz, astrid@maths.otago.ac.nz
ASTRID AN HUEF
Affiliation:
Department of Mathematics and Statistics, University of Otago, PO Box 56, Dunedin 9054, New Zealand. e-mail: lclark@maths.otago.ac.nz, astrid@maths.otago.ac.nz
Get access Rights & Permissions [Opens in a new window]

Abstract

Let E be a second-countable, locally compact, Hausdorff groupoid equipped with an action of such that G: = E/ is a principal groupoid with Haar system λ. The twisted groupoid C*-algebra C*(E; G, λ) is a quotient of the C*-algebra of E obtained by completing the space of -equivariant functions on E. We show that C*(E; G, λ) is postliminal if and only if the orbit space of G is T0 and that C*(E; G, λ) is liminal if and only if the orbit space is T1. We also show that C*(E; G, λ) has bounded trace if and only if G is integrable and that C*(E; G, λ) is a Fell algebra if and only if G is Cartan.

Let 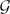be a second-countable, locally compact, Hausdorff groupoid with Haar system λ and continuously varying, abelian isotropy groups. Let 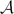be the isotropy groupoid and 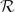: = 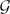/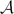. Using the results about twisted groupoid C*-algebras, we show that the C*-algebra C*(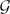, λ) has bounded trace if and only if 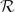is integrable and that C*(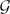, λ) is a Fell algebra if and only if 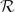is Cartan. We illustrate our theorems with examples of groupoids associated to directed graphs.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 153 , Issue 1 , July 2012 , pp. 167 - 191
Copyright
Copyright © Cambridge Philosophical Society 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Archbold, R. J. and an Huef, A.Strength of convergence in the orbit space of a transformation group. J. Funct. Anal. 235 (2006), 90–121.Google Scholar
[2]Archbold, R. J. and an Huef, A.Strength of convergence and multiplicities in the spectrum of a C*-dynamical system. Proc. London Math. Soc. 96 (2008), 545–581.CrossRefGoogle Scholar
[3]Archbold, R. J. and Somerset, D. W. B.Transition probabilities and trace functions for C*-algebras. Math. Scand. 73 (1993), 81–111.Google Scholar
[4]Clark, L. O.Classifying the type of principal groupoid C*-algebras. J. Operator Theory. 57 (2007), 251–266.Google Scholar
[5]Clark, L. O.CCR and GCR Groupoid C*-algebras. Indiana Univ. Math. J. 56 (2007), 2087–2110.Google Scholar
[6]Clark, L. O. and an Huef, A.Principal groupoid C*-algebras with bounded trace. Proc. Amer. Math. Soc. 136 (2008), 623–634.Google Scholar
[7]Dixmier, J.C*-algebras. (North-Holland, 1977).Google Scholar
[8]Echterhoff, S.On transformation group C*-algebras with continuous trace. Trans. Amer. Math. Soc. 343 (1994), 117–133.Google Scholar
[9]Ephrem, M.Characterizing liminal and type I graph C*-algebras. J. Operator Theory. 52 (2004), 303–323.Google Scholar
[10]Glimm, J.Locally compact transformation groups. Trans. Amer. Math. Soc. 101 (1961), 124–128.CrossRefGoogle Scholar
[11]Gootman, E. C.The type of some C*- and W*-algebras associated with transformation groups. Pacific J. Math. 48 (1973), 93–106.Google Scholar
[12]Green, P.C*-algebras of transformation groups with smooth orbit space. Pacific J. Math. 72 (1977), 71–97.Google Scholar
[13]Hazlewood, R. Classifying higher-rank graph algebras using the path groupoid. In preparation.Google Scholar
[14]Hazlewood, R. and an Huef, A.The strength of convergence in the orbit space of a groupoid. J. Math. Anal. Appl. 383 (2011), 1–24.Google Scholar
[15]an Huef, A.The transformation groups whose C*-algebras are Fell algebras. Bull. London Math. Soc. 33 (2001), 73–76.Google Scholar
[16]an Huef, A.Integrable actions and the transformation groups whose C*-algebras have bounded trace. Indiana Univ. Math. J. 51 (2002), 1197–1233.Google Scholar
[17]Kumjian, A.On C*-diagonals. Canad. J. Math. 38 (1986), 969–1008.Google Scholar
[18]Kumjian, A., Pask, D., Raeburn, I. and Renault, J.Graphs, groupoids and Cuntz–Krieger algebras. J. Funct. Anal. 144 (1997), 505–541.Google Scholar
[19]Muhly, P. S. and Williams, D. P.Continuous trace groupoid C*-algebras. Math. Scand. 66 (1990), 231–241.Google Scholar
[20]Muhly, P. S. and Williams, D. P.Continuous trace groupoid C*-algebras II. Math. Scand. 70 (1992), 127–145.Google Scholar
[21]Muhly, P. S., Renault, J. and Williams, D. P.Continuous trace groupoid C*-algebras, III. Trans. Amer. Math. Soc. 348 (1996), 3621–3641.CrossRefGoogle Scholar
[22]Pedersen, G. K.C*-algebras and their automorphism groups. (Academic Press, 1979).Google Scholar
[23]Raeburn, I. and Williams, D. P. Morita equivalence and continuous-trace C*-Algebras. Math. Surveys and Monographs, vol. 60 (Amer. Math. Soc., 1998).Google Scholar
[24]Ramsay, A.The Mackey–Glimm dichotomy for foliations and other Polish groupoids. J. Funct. Anal. 94 (1990), 358–374.Google Scholar
[25]Renault, J. A groupoid approach to C*-algebras. Lecture Notes in Math. No. 793 (Springer-Verlag, 1980).Google Scholar
[26]Renault, J.Représentations des produits croisés d'algèbres de groupoides. J. Operator Theory 18 (1987), 67–97.Google Scholar
[27]Renault, J.The ideal structure of groupoid crossed product C*-algebras. J. Operator Theory 25 (1991), 3–36.Google Scholar
[28]Williams, D. P.The topology on the primitive ideal space of transformation group C*-algebras and CCR transformation group C*-algebras. Trans. Amer. Math. Soc. 266 (1981), 335–359.Google Scholar
[29]Williams, D. P.Transformation group C*-algebras with continuous trace. J. Funct. Anal. 41 (1981), 40–76.Google Scholar
[30]Williams, D. P. Crossed products of C*-algebras. Math. Surveys and Monographs, vol. 134 (Amer. Math. Soc., 2007).Google Scholar