Hostname: page-component-77c89778f8-m42fx Total loading time: 0 Render date: 2024-07-18T10:57:26.537Z Has data issue: false hasContentIssue false
  • English
  • Français

Radial variation of analytic functions with non-tangential boundary limits almost everywhere

Published online by Cambridge University Press:  24 October 2008

D. J. Hallenbeck  and
K. Samotij
D. J. Hallenbeck
Affiliation:
Department of Mathematical Sciences, University of Delaware, Newark, Delaware 19716, U.S.A.
K. Samotij
Affiliation:
Instytut Matematyki, Politechniki Wrocławskiej, Wybrzeże St. Wyspiańskiego 27, 50-370 Wroclaw, Poland
Get access Rights & Permissions [Opens in a new window]

Extract

The purpose of this paper is to investigate the asymptotic behaviour as r → 1− of the integrals

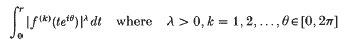
and f is an analytic function on the unit disk Δ which has non-tangential limits at almost every point on ∂Δ. The paper is divided into three parts. In the first part we consider the case where λ ≠ 1/k, in the second the somewhat more delicate case when λ = 1/k and in the third part we concentrate on some problems related to the case λ = k = 1.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 108 , Issue 2 , September 1990 , pp. 371 - 379
Copyright
Copyright © Cambridge Philosophical Society 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baernstein, A.. Analytic functions of bounded mean oscillation. In Aspects of Contemporary Complex Analysis (Academic Press, 1980), pp. 3–36.Google Scholar
[2]Hallenbeck, D. J. and MacGregor, T. H.. Radial growth and variation of bounded analytic functions. Proc. Edinburgh Math. Soc. 31 (1988), 489–498.CrossRefGoogle Scholar
[3]Hallenbeck, D. J. and Samotij, K.. Radial growth and variation of Dirichlet finite holomorphic functions in the disk. Colloq. Math. (To appear.)Google Scholar
[4]Hallenbeck, D. J. and Samotij, K.. On radial variation of holomorphic functions with lp Taylor coefficients. (To appear.)Google Scholar
[5]Hallenbeck, D. J. and Samotij, K.. On radial variation of bounded analytic functions. (To appear.)Google Scholar
[6]Jack, I. S.. Functions starlike and convex of order α. J. London Math. Soc. (2) 3 (1971), 469–474.CrossRefGoogle Scholar
[7]Rudin, W.. The radial variation of analytic functions. Duke Math. J. 22 (1955), 235–242.CrossRefGoogle Scholar
[8]Zygmund, A.. On certain integrals. Trans. Amer. Math. Soc. 55 (1944), 170–204.CrossRefGoogle Scholar
[9]Zygmund, A.. Trigonometric series, vol. 2, 2nd edition (Cambridge University Press, 1968).Google Scholar