Hostname: page-component-848d4c4894-xfwgj Total loading time: 0 Render date: 2024-07-06T02:28:14.390Z Has data issue: false hasContentIssue false
  • English
  • Français

The power inequality on Banach spaces

Published online by Cambridge University Press:  24 October 2008

Béla Bollobás
Béla Bollobás
Affiliation:
Trinity College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

Let X be a complex normed space with dual space X′ and let T be a bounded linear operator on X. The numerical range of T is defined as

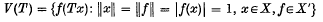
and the numerical radius is v(T) = sup {|ν: νε V(T)}. Most known results and problems concerning numerical range can be found in the notes by Bonsall and Duncan (5).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 69 , Issue 3 , May 1971 , pp. 411 - 415
Copyright
Copyright © Cambridge Philosophical Society 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Berger, C. A. On the numerical range of an operator. Bull. Amer. Math. Soc. (to appear).Google Scholar
(2)Berger, C. A. and Stampfli, J. G.Mapping theorems for the numerical range. Amer. J. Math. 89 (1967), 1047–1055.CrossRefGoogle Scholar
(3)Bohnenblust, H. F. and Karlin, S.Geometrical properties of the unit sphere of Banach algebras. Ann. of Math. 62 (1955), 217–229.CrossRefGoogle Scholar
(4)Bonsall, F. F.The numerical range of an element of a normed algebra. Glasgow Math. J. 10 (1969), 68–72.CrossRefGoogle Scholar
(5)Bonsall, F. F. and Duncan, J. Numerical range. London Math. Soc. Lecture Note Series (to appear).Google Scholar
(6)Crebb, M. J. Numerical range estimates for the norms of iterated operators. Glasgow Math. J. (to appear).Google Scholar
(7)Glickfeld, B. W.On an inequality of Banach algebra geometry and semi-inner-product space theory. Notices Amer. Math. Soc. 15 (1968), 339–340.Google Scholar
(8)Halmos, P. R.Introduction to Hubert space and the theory of 8pectral multiplicity (Chelsea; New York, 1951).Google Scholar
(9)Halmos, P. R.Hubert space problem book (Van Nostrand, 1967).Google Scholar
(10)Kato, T.Some mapping theorems for the numerical range. Proc. Japan Acad. 41 (1965), 652–655.Google Scholar
(11)Lumer, G.Semi-inner-product spaces. Trans. Amer. Math. Soc. 100 (1961), 29–43.CrossRefGoogle Scholar
(12)Pearcy, C.An elementary proof of the power inequality for the numerical radius. Michigan Math. J. 13 (1966), 289–291.CrossRefGoogle Scholar