Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hoa, Le Tuan
and
Trung, Tran Nam
2016.
Castelnuovo-Mumford regularity of symbolic powers of two-dimensional square-free monomial ideals.
Journal of Commutative Algebra,
Vol. 8,
Issue. 1,
Trung, Tran Nam
2016.
Stability of depths of powers of edge ideals.
Journal of Algebra,
Vol. 452,
Issue. ,
p.
157.
Seyed Fakhari, S.A.
2017.
Depth and Stanley depth of symbolic powers of cover ideals of graphs.
Journal of Algebra,
Vol. 492,
Issue. ,
p.
402.
Hoa, Le Tuan
Kimura, Kyouko
Terai, Naoki
and
Trung, Tran Nam
2017.
Stability of depths of symbolic powers of Stanley–Reisner ideals.
Journal of Algebra,
Vol. 473,
Issue. ,
p.
307.
Hoa, Le Tuan
and
Trung, Tran Nam
2018.
Stability of Depth and Cohen-Macaulayness of Integral Closures of Powers of Monomial Ideals.
Acta Mathematica Vietnamica,
Vol. 43,
Issue. 1,
p.
67.
Dao, Hailong
De Stefani, Alessandro
Grifo, Eloísa
Huneke, Craig
and
Núñez-Betancourt, Luis
2018.
Singularities and Foliations. Geometry, Topology and Applications.
Vol. 222,
Issue. ,
p.
387.
Hang, Nguyen Thu
and
Trung, Tran Nam
2018.
Regularity of powers of cover ideals of unimodular hypergraphs.
Journal of Algebra,
Vol. 513,
Issue. ,
p.
159.
Minh, Nguyên Công
and
Trung, Trân Nam
2019.
Regularity of symbolic powers and arboricity of matroids.
Forum Mathematicum,
Vol. 31,
Issue. 2,
p.
465.
Nguyen, Hop Dang
and
Trung, Ngo Viet
2019.
Depth functions of symbolic powers of homogeneous ideals.
Inventiones mathematicae,
Vol. 218,
Issue. 3,
p.
779.
Seyed Fakhari, S. A.
2019.
Stability of depth and Stanley depth of symbolic powers of squarefree monomial ideals.
Proceedings of the American Mathematical Society,
Vol. 148,
Issue. 5,
p.
1849.
Seyed Fakhari, S. A.
2020.
Combinatorial Structures in Algebra and Geometry.
Vol. 331,
Issue. ,
p.
143.
Kustin, Andrew R.
Polini, Claudia
and
Ulrich, Bernd
2020.
Degree bounds for local cohomology.
Proceedings of the London Mathematical Society,
Vol. 121,
Issue. 5,
p.
1251.
Công Minh, Nguyên
and
Thi Thuy, Phan
2020.
A computation of the Castelnuovo-Mumford regularity of certain two-dimensional unmixed ideals.
Communications in Algebra,
Vol. 48,
Issue. 5,
p.
2028.
Kumar, Arvind
Kumar, Rajiv
Sarkar, Rajib
and
Selvaraja, S.
2021.
Symbolic Powers of Certain Cover Ideals of Graphs.
Acta Mathematica Vietnamica,
Vol. 46,
Issue. 3,
p.
599.
Dung, Le Xuan
Hien, Truong Thi
Nguyen, Hop D.
and
Trung, Tran Nam
2021.
Regularity and Koszul property of symbolic powers of monomial ideals.
Mathematische Zeitschrift,
Vol. 298,
Issue. 3-4,
p.
1487.
Montaño, Jonathan
and
Núñez-Betancourt, Luis
2021.
Splittings and Symbolic Powers of Square-free Monomial Ideals.
International Mathematics Research Notices,
Vol. 2021,
Issue. 3,
p.
2304.
Hoa, Le Tuan
2022.
Maximal generating degrees of integral closures of powers of monomial ideals.
Journal of Algebraic Combinatorics,
Vol. 56,
Issue. 2,
p.
279.
Hoa, Le Tuan
2022.
Asymptotic behavior of integer programming and the stability of the Castelnuovo–Mumford regularity.
Mathematical Programming,
Vol. 193,
Issue. 1,
p.
157.
De Stefani, Alessandro
Montaño, Jonathan
and
Núñez-Betancourt, Luis
2023.
Frobenius methods in combinatorics.
São Paulo Journal of Mathematical Sciences,
Vol. 17,
Issue. 1,
p.
387.
Seyed Fakhari, S.A.
2024.
Lower bounds for the depth of symbolic powers of edge ideals of graphs.
Journal of Algebra,
Vol. 639,
Issue. ,
p.
422.
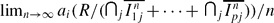 also exist.
also exist.



