Hostname: page-component-7479d7b7d-t6hkb Total loading time: 0 Render date: 2024-07-12T02:05:28.275Z Has data issue: false hasContentIssue false
  • English
  • Français

On the set of the logarithm of the LMO invariant for integral homology 3-spheres

Published online by Cambridge University Press:  01 September 2008

TOSHIE TAKATA
TOSHIE TAKATA*
Affiliation:
Department of Mathematics, Faculty of Science, Niigata University, Niigata 950-2181, Japan. e-mail: takata@math.sc.niigata-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

The LMO invariant is a very strong invariant such that it is expected to classify integral homology 3-spheres. In this paper we identify the set of the degree ≤ 6 parts of the logarithm of the LMO invariant for integral homology 3-spheres. As an application, we obtain a complete set of relations which characterize the set of Ohtsuki's invariants {λi(M)} for i ≤ 6. For any simple Lie algebra 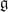, we also obtain a complete set of relations which characterize the set of perturbative P 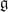invariants {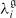(M)} for i ≤ 3.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 145 , Issue 2 , September 2008 , pp. 349 - 361
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bar–Natan, D.. On the Vassiliev knot invariant. Topology 34 (1995), 423–472.CrossRefGoogle Scholar
[2]Bar–Natan, D., Garoufalidis, S., Rozansky, L. and Thurston, D. P.. The Århus integral of rational homology 3-speres, part I. Selecta Math.(N.S) 8 (2002), 315–339.CrossRefGoogle Scholar
[3]Bar–Natan, D. and Lawrence, R.. A rational surgery formula for the LMO invariant. Israel J. Math. 140 (2004), 29–60.CrossRefGoogle Scholar
[4]Habiro, K.. Claspers and finite type invariants of links. Geometry and Topology 4 (2000), 1–83.CrossRefGoogle Scholar
[5]Habiro, K.. A unified Witten–Reshetikhin-Turaev invariant for integral homolgy spheres (2006), (arXiv:math.GT/0605314).CrossRefGoogle Scholar
[6]Jackson, D. M., Moffatt, I. and Morales, A.. On the group-like behaviour of the Le–Murakami–Ohtsuki invariant (2005) (arXiv:math.GA/0511452).Google Scholar
[7]Kneissler, J. A.. The number of primitive vassiliev invariants up to degree 12 (1997), (arXiv:math.QA/9706022).Google Scholar
[8]Lawrence, R.. On Ohtsuki's invariants of homolgy 3-spheres. J. Knot Theory Ramifications 8 (1999), no. 8, 1049–1063.CrossRefGoogle Scholar
[9]Lawrence, R. and Rozansky, L.. Witten–Reshetikhin–Turaev invariants of seifert manifolds. Commun. Math. Phys. 205 (1999), no. 2, 287–314.CrossRefGoogle Scholar
[10]Le, T. T. Q.. An invariant of integral homology 3-spheres which is universal for all finite type invariants. Solitons, geometry, and topology: on the crossroad (Providence, RI) Amer. Math. Soc. Transl. Ser. 2, vol. 179 (Amer. Math. Soc., 1997), pp. 75–100.Google Scholar
[11]Le, T. T. Q., Murakami, J. and Ohtsuki, T.. On a universal perturbative invariant of 3-manifolds. Topology 37 (1998), no. 3, 539–574.CrossRefGoogle Scholar
[12]Le, T. T. Q.. On denominators of the kontsevich integral and the universal perturbative invariant of 3-manifolds. Invent. 135 (1999), 689–722.CrossRefGoogle Scholar
[13]Le, T. T. Q.. On perturbative PSU(n) invariants of rational homology 3-spheres. Topology 39 (2000), 813–849.CrossRefGoogle Scholar
[14]Lin, X.-S. and Wang, Z.. Fermat limit and congruence of Ohtsuki invariants. Proceedings of the Kirbyfest, Geometry and Topology Monographs 2 (1999) 321–333.CrossRefGoogle Scholar
[15]Lin, X.-S. and Wang, Z.. On Ohtsuki's invariants of integral homology 3-spheres. Acta Math. Sinica Series B 15 (1999), 293–316.CrossRefGoogle Scholar
[16]Mariño, M.. Chern-simons theory, matrix integrals, and perturbative three manifold invariants. Commun. Math. Phys 253 (2005), 25–49.CrossRefGoogle Scholar
[17]Murakami, H.. Quantum SU(2)-invariants dominate Casson's SU(2)-invariant. Math. Proc. Cambridge Phil. Soc. 115 (1993), 253–281.CrossRefGoogle Scholar
[18]Ohtsuki, T.. A polynomial invariant of integral homology 3-spheres. Math. Proc. Camb. Phil. Soc. 117 (1995), no. 1, 83–112.CrossRefGoogle Scholar
[19]Ohtsuki, T.. The perturbative SO(3) invariant of rational homology 3-spheres recovers from the universal perturbative invariant. Topology 39 (2000), 1103–1135.CrossRefGoogle Scholar
[20]Ohtsuki, T.. Quantum invariants. A study of knots, 3-manifolds, their sets. Series on Knots and Everything, vol. 29 (World Ccientific Publishing Co., Inc., 2002).CrossRefGoogle Scholar
[21]Rozansky, L.. On p-adic propreties of the Witten-Reshetikhin-Turaev invariant (1998), (arXiv:math.QA/9806075).Google Scholar
[22]Takata, T.. On quantum PSU(N) invariants for Seifert manifolds. J. Knot Theory Ramifications 6 (1997), 417–426.CrossRefGoogle Scholar
[23]Vogel, P.. Algebraic structures on modules of diagrams. To appear in Invent. Math., available at http://www.math.jussieu.fr/vogel/.Google Scholar
[24]Witten, E.. Quantum field theory and the Jones polynomial. Comm. Math. Phys. 121 (1989), 351–399.CrossRefGoogle Scholar