Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-28T13:50:34.531Z Has data issue: false hasContentIssue false
  • English
  • Français

On the connexion between Hausdorff measures and generalized capacity

Published online by Cambridge University Press:  24 October 2008

S. J. Taylor
S. J. Taylor
Affiliation:
Cornell University and Birmingham University
Get access Rights & Permissions [Opens in a new window]

Extract

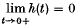For any real function h(t) which is continuous and monotonic increasing for t > 0 with , Hausdorff (10) in 1918 denned a Carathéodory measure with respect to h(t) which has subsequently been known as Hausdorff measure. For analysing sets in Euclidean space, these measures have proved both useful and interesting. Given a real function Φ(t) which is continuous and monotonic decreasing for t > 0 with 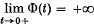, Frostman(9) in 1935 denned capacity with respect to Φ(t). Lebesgue measure in Euclidean k-space is a special case of Hausdorff measure, and capacity with respect to Φ(t) becomes logarithmic capacity or Newtonian capacity in the cases 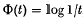, Φ(t)=1/t, respectively. The interrelationship between h-measure and Φ-capacity has been of interest in both directions: (i) in applications to function theory one may be able to determine whether or not a set has positive capacity by examining the h-measure for suitable h(t) (see, for example, (5)); (ii) it may be possible to determine the measure properties of a set from knowledge of its capacity (see, for example, (7) and (17)).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 3 , July 1961 , pp. 524 - 531
Copyright
Copyright © Cambridge Philosophical Society 1961

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Besicovitch, A. S.On existence of subsets of finite measure of sets of infinite measure. Indag. Math. 14 (1952), 339–44.CrossRefGoogle Scholar
(2)Carleson, L. On a class of meromorphic functions and its associated exceptional sets (Thesis, Uppsala, 1950).Google Scholar
(3)Carleson, L.on the connection between Hausdorff measures and capacity. Arkiv Math. 3 (1957), 403–6.CrossRefGoogle Scholar
(4)Davies, R. O.Non σ-finite closed subsets of analytic sets. Proc. Camb. Phil. Soc. 52 (1956), 174–7.CrossRefGoogle Scholar
(5)Dvoretsky, A., Ebdős, P., Kakutani, S. and Taylor, S. J.Triple points of Brownian paths in 3-space. Proc. Camb. Phil. Soc. 53 (1957), 856–62.CrossRefGoogle Scholar
(6)Ebdős, P. and Gillis, J.Note on the transfinite diameter. J. Lond. Math. Soc. 12 (1937), 185–92.Google Scholar
(7)Ebdős, P. and Taylor, S. J.On the Hausdorff measure of Brownian paths in the plane. Proc. Camb. Phil. Soc. 57 (1961), 209–22.Google Scholar
(8)Fekete, M.Über den transfiniten Durchmesser ebener Punktmengen. I. Math. Z. 32 (1930), 108–14.CrossRefGoogle Scholar
(9)Frostman, O.Potentiel d'équilibre et capacité des ensembles, avec quelques applications a la théorie des fonctions. Medd. Lunds Univ. Mat. Semin. 3 (1935).Google Scholar
(10)Hausdorff, F.Dimension und äuseres Mass. Math. Ann. 79 (1918), 157–79.CrossRefGoogle Scholar
(11)Kametani, S.On some properties of Hausdorff's measure and the concept of capacity in generalized potentials. Proc. Imp. Acad. Japan, 18 (1942), 617–25.Google Scholar
(12)Kametani, S.On Hausdorff's measures and generalized capacities with some of their applications to the theory of functions. Japanese J. Math. 19 (1944), 217–57.CrossRefGoogle Scholar
(13)Kametani, S.A note on a metric property of capacity. Nat. Sci. Rep. Ochanomizu Univ. 4 (1953), 51–4.Google Scholar
(14)Lindeberg, J. W.Sur l'existence de fonctions d'une variable complexe et de fonctions holomorphes bornées. Ann. Acad. Sci. Fennicae, Ser. A, 11 (1918), no. 6.Google Scholar
(15)Myrbebg, P. J.Über die Existenz der Greenschen Funktionen auf einer gegebenen Riemannschen Flache. Acta Math. 61 (1933), 39–79.CrossRefGoogle Scholar
(16)Nevanlinna, R.Über die Kapazitat der Cantorschen Punktmengen. Mb. Math. Phys. 43 (1936), 435–47.CrossRefGoogle Scholar
(17)Taylor, S. J.The α-dimensional measure of the graph and set of zeros of a Brownian path. Proc. Camb. Phil. Soc. 51 (1955), 265–74.CrossRefGoogle Scholar
(18)Ugaheri, T.On the Newtonian capacity and the linear measure. Proc. Imp. Acad. Japan, 18 (1942), 602–5.Google Scholar
(19)Ursell, H. D.Note on the transfinite diameter. J. Lond. Math. Soc. 13 (1938), 34–7.CrossRefGoogle Scholar