Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-27T16:56:32.415Z Has data issue: false hasContentIssue false
  • English
  • Français

On parallelepipeds of minimal volume containing a convex symmetric body in ℝn

Published online by Cambridge University Press:  24 October 2008

A. Pelczynski  and
S. J. Szarek
A. Pelczynski
Affiliation:
Institute of Mathematics, Polish Academy of Sciences, Sniadeckich 8, Ip., 00950 Warszawa, Poland
S. J. Szarek
Affiliation:
Department of Mathematics, Case Western Reserve University, Cleveland Ohio 44106, U.S.A. Institut des Hautes Etudes Scientifiques, 91440 Bures-Sur-Yvette, France
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a convex symmetric body C ⊂ ℝn we put a(C) = |C| sup |P|−1 where the supremum extends over all parallelepipeds containing C and |A| denotes the volume of a set A ⊂ ℝn. Let an = inf {a(C): C ⊂ ℝn}. We show that

which slightly improves the estimate due to Dvoretzky and Rogers [6]. In every dimension n we construct a convex symmetric polytope Wn such that the unit Euclidean ball is the ellipsoid of maximal volume inscribed into Wn and the volume of every parallelepiped containing Wn is greater than

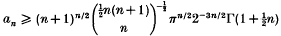
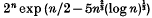
for large n which shows ‘the limit’ to the Dvoretzky Rogers method for bounding an below. We present an alternative proof of the result of I. K. Babenko [l] that . We show that 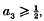, and that a local minimum of the function C→a(C) for C ⊂ ℝn is attained only at an equiframed convex body (that is, a body such that every point of its boundary belongs to a parallelepiped of minimal volume containing the body).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 109 , Issue 1 , January 1991 , pp. 125 - 148
Copyright
Copyright © Cambridge Philosophical Society 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Babenko, I. K.. Asymptotic volume of tori and geometry of convex bodies. Mat. Zametki 44 (1988), 177–190.Google Scholar
[2]Ball, K.. Volumes of sections of cubes and related problems. In Geometric Aspects of Functional Analysis, Lecture Notes in Math. vol. 1376 (Springer-Verlag, 1989), pp. 251–260.CrossRefGoogle Scholar
[3]Beckenbach, E. and Bellman, R.. Inequalities (Springer-Verlag, 1961).CrossRefGoogle Scholar
[4]Chaladus, S. and Teterin, Yu.. Note on a decomposition of integer vectors, II. Acta Arith. 57 (To appear.)CrossRefGoogle Scholar
[5]Day, M. M.. Polygons circumscribed about closed convex curves. Trans. Amer. Math. Soc. 62 (1947), 315–319.CrossRefGoogle Scholar
[6]Dvoretzky, A. and Rogers, C. A.. Absolute and unconditional convergence in normed linear spaces. Proc. Nat. Acad. Sci. U.S.A. 36 (1950), 192–197.CrossRefGoogle ScholarPubMed
[7]Geiss, S.. Antisymmetric tensor products of absolutely p-summing operators. Ph.D. thesis, University of Jena (1990).Google Scholar
[8]John, F.. Extremum problems with inequalities as subsidiary conditions. In Courant Aniversary Volume (Interscience, 1948), pp. 187–204.Google Scholar
[9]Kashin, B. S.. On parallelepipeds of minimal volume containing a convex body (Russian), Mat. Zametki 45 (1989), 134–135.Google Scholar
[10]Leichtweiss, K.. Konvexe Mengen (Springer-Verlag, 1980).CrossRefGoogle Scholar
[11]Lewis, D. R.. Ellipsoids defined by Banach ideal norms. Mathematika 26 (1979), 18–29.CrossRefGoogle Scholar
[12]Milman, V. D. and Schechtman, G.. Finite-Dimensional Normed Spaces. Lecture Notes in Math. vol. 1200 (Springer-Verlag, 1986).Google Scholar
[13]Schinzel, A.. A decomposition of integer vectors, III. Bull. Polish. Acad. Sci. Ser. Math. 35 (1987), 693–703.Google Scholar
[14]Schinzel, A.. A decomposition of integer vectors, IV. J. Austral. Math. Soc. (To appear.)Google Scholar
[15]Taylor, A. E.. A geometric theorem and its application to biorthogonal systems. Bull. Amer. Math. Soc. 53 (1947), 614–616.CrossRefGoogle Scholar
[16]Titchmarsh, E. C.. The Theory of Functions, second edition (Oxford University Press, 1939).Google Scholar
[17]Tomczak-Jaegermann, N.. Banach–Mazur Distances and Finite Dimensional Operator Ideals (Longman, 1989).Google Scholar