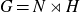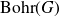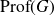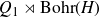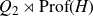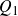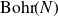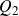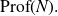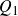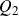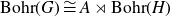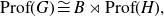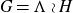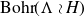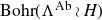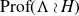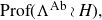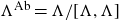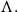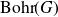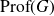1. Introduction
There are two distinguished compact groups associated to a general topological group G. A Bohr compactification (respectively, a profinite completion) of G is a pair consisting of a compact (respectively, profinite) group K and a continuous homomorphism
![]() $\beta\,:\, G \to K $
with dense image satisfying the following universal property: for every compact group (respectively, profinite group) L and every continuous homomorphism
$\beta\,:\, G \to K $
with dense image satisfying the following universal property: for every compact group (respectively, profinite group) L and every continuous homomorphism
![]() $\alpha\,:\, G \to L$
, there exists a continuous homomorphism
$\alpha\,:\, G \to L$
, there exists a continuous homomorphism
![]() $\alpha'\,:\, K\to L$
such that the diagram
$\alpha'\,:\, K\to L$
such that the diagram

commutes. Bohr compactifications and profinite completions
![]() $(K, \beta) $
of G are unique in the following sense: if
$(K, \beta) $
of G are unique in the following sense: if
![]() $(K', \beta')$
is a pair consisting of a compact (respectively, profinite) group K’ and a continuous homomorphism
$(K', \beta')$
is a pair consisting of a compact (respectively, profinite) group K’ and a continuous homomorphism
![]() $\beta'\,:\, G \to K'$
with dense image satisfying the same universal property, then there exists an isomorphism
$\beta'\,:\, G \to K'$
with dense image satisfying the same universal property, then there exists an isomorphism
![]() $f\,:\, K \to K'$
of topological groups such that
$f\,:\, K \to K'$
of topological groups such that
![]() $\beta' = f \circ \beta$
. Concerning existence, we give below (Proposition 4) models of Bohr compactifications and profinite completions. For more on Bohr compactifications, see [
Reference DixmierDix77
, section 16], [
Reference Bekka and de la HarpeBdlH
, 4·C] or [
Reference WeilWei40
, chapter VII]; for more details on profinite completions, see [
Reference Ribes and ZalesskiiRZ00
].
$\beta' = f \circ \beta$
. Concerning existence, we give below (Proposition 4) models of Bohr compactifications and profinite completions. For more on Bohr compactifications, see [
Reference DixmierDix77
, section 16], [
Reference Bekka and de la HarpeBdlH
, 4·C] or [
Reference WeilWei40
, chapter VII]; for more details on profinite completions, see [
Reference Ribes and ZalesskiiRZ00
].
We will often denote by
![]() $({\rm Bohr}(G), \beta_G)$
and
$({\rm Bohr}(G), \beta_G)$
and
![]() $({\rm Prof}(G), \alpha_G)$
a Bohr compactification and a profinite completion of G. In the sequel, for two topological groups H and L, we write
$({\rm Prof}(G), \alpha_G)$
a Bohr compactification and a profinite completion of G. In the sequel, for two topological groups H and L, we write
![]() $H\cong L$
if H and L are topologically isomorphic.
$H\cong L$
if H and L are topologically isomorphic.
The universal property of
![]() ${\rm Bohr}(G)$
gives rise to a continuous surjective homomorphism
${\rm Bohr}(G)$
gives rise to a continuous surjective homomorphism
![]() $\alpha\,:\, {\rm Bohr}(G) \to {\rm Prof}(G)$
such that
$\alpha\,:\, {\rm Bohr}(G) \to {\rm Prof}(G)$
such that
![]() $\alpha_G = \alpha \circ \beta_G$
. It is easy to see (see [
Reference BekkaBek23
, proposition 7]) that the kernel of
$\alpha_G = \alpha \circ \beta_G$
. It is easy to see (see [
Reference BekkaBek23
, proposition 7]) that the kernel of
![]() $\alpha$
is
$\alpha$
is
![]() ${\rm Bohr}(G)_0$
, the connected component of
${\rm Bohr}(G)_0$
, the connected component of
![]() ${\rm Bohr}(G),$
and so
${\rm Bohr}(G),$
and so
Every continuous homomorphism
![]() $G_1 \xrightarrow{f} G_2$
of topological groups induces continuous homomorphisms
$G_1 \xrightarrow{f} G_2$
of topological groups induces continuous homomorphisms
such that
![]() $\beta_{G_2} \circ f= {\rm Bohr}(\,f)\circ\beta_{G_1}$
and
$\beta_{G_2} \circ f= {\rm Bohr}(\,f)\circ\beta_{G_1}$
and
![]() $\alpha_{G_2} \circ f= {\rm Prof}(\,f)\circ\alpha_{G_1}.$
$\alpha_{G_2} \circ f= {\rm Prof}(\,f)\circ\alpha_{G_1}.$
Consider the category TGrp of topological groups, with objects the topological groups and morphisms the continuous homomorphisms between topological groups. The Bohr compactification and the profinite completion are covariant functors
from TGrp to the subcategory CGrp of compact groups and the subcategory PGrp of profinite groups.
Assume that we are given an extension
of topological groups. The functors
![]() ${\rm Bohr}$
and
${\rm Bohr}$
and
![]() ${\rm Prof}$
are right exact and so the diagrams
${\rm Prof}$
are right exact and so the diagrams
and
are exact; this means that
where
![]() $\overline{A}$
denotes the closure of a subset A; these facts are well known and easy to prove (see, e.g., [
Reference Hart and KunenHK01
, lemma 2·2] and [
Reference Ribes and ZalesskiiRZ00
, proposition 3·2·5]; see also Proposition 7 below). However, the functors
$\overline{A}$
denotes the closure of a subset A; these facts are well known and easy to prove (see, e.g., [
Reference Hart and KunenHK01
, lemma 2·2] and [
Reference Ribes and ZalesskiiRZ00
, proposition 3·2·5]; see also Proposition 7 below). However, the functors
![]() ${\rm Bohr}$
and
${\rm Bohr}$
and
![]() ${\rm Prof}$
are not left exact, that is,
${\rm Prof}$
are not left exact, that is,
![]() ${\rm Bohr}(i)\,:\, {\rm Bohr}(N) \to {\rm Bohr}(G)$
and
${\rm Bohr}(i)\,:\, {\rm Bohr}(N) \to {\rm Bohr}(G)$
and
![]() ${\rm Prof}(i)\,:\, {\rm Prof}(N) \to {\rm Prof}(G)$
are in general not injective (see e.g. the examples given by Corollaries F and G below).
${\rm Prof}(i)\,:\, {\rm Prof}(N) \to {\rm Prof}(G)$
are in general not injective (see e.g. the examples given by Corollaries F and G below).
For now on, we will deal only with locally compact groups. and with split extensions. So, we will consider locally compact groups
![]() $G=N\rtimes H$
which are a semi-direct product of a normal closed subgroup N and a closed subgroup H. It is easy to see that
$G=N\rtimes H$
which are a semi-direct product of a normal closed subgroup N and a closed subgroup H. It is easy to see that
![]() ${\rm Bohr}(G)$
, respectively
${\rm Bohr}(G)$
, respectively
![]() ${\rm Prof}(G)$
, is a semi-direct product of
${\rm Prof}(G)$
, is a semi-direct product of
![]() $\overline{\beta_G(N)}$
with
$\overline{\beta_G(N)}$
with
![]() $\overline{\beta_G(H)}$
, respectively of
$\overline{\beta_G(H)}$
, respectively of
![]() $\overline{\alpha_G(N)}$
with
$\overline{\alpha_G(N)}$
with
![]() $\overline{\alpha_G(H)}$
(see [
Reference JunghennJun78
,
Reference Grunewald and ZalesskiiGZ11
]). Our results give a precise description of the structure of these semi-direct products.
$\overline{\alpha_G(H)}$
(see [
Reference JunghennJun78
,
Reference Grunewald and ZalesskiiGZ11
]). Our results give a precise description of the structure of these semi-direct products.
Denote by
![]() $\widehat{N}_{ \rm fd}$
the set of equivalence classes (modulo unitary equivalence) of irreducible finite dimensional unitary representations of N. Every such representation
$\widehat{N}_{ \rm fd}$
the set of equivalence classes (modulo unitary equivalence) of irreducible finite dimensional unitary representations of N. Every such representation
![]() $\sigma\,:\, N\to U(n)$
gives rise to the unitary representation
$\sigma\,:\, N\to U(n)$
gives rise to the unitary representation
![]() ${\rm Bohr}({\sigma})\,:\,{\rm Bohr}(N)\to U(n) $
of
${\rm Bohr}({\sigma})\,:\,{\rm Bohr}(N)\to U(n) $
of
![]() ${\rm Bohr}(N)$
; here (and elsewhere) we identify
${\rm Bohr}(N)$
; here (and elsewhere) we identify
![]() ${\rm Bohr}(U(n))$
with
${\rm Bohr}(U(n))$
with
![]() $U(n).$
$U(n).$
Observe that H acts on
![]() $ \widehat{N}_{\rm fd}$
: for
$ \widehat{N}_{\rm fd}$
: for
![]() $\sigma\in \widehat{N}_{\rm fd}$
and
$\sigma\in \widehat{N}_{\rm fd}$
and
![]() $h\in H,$
the conjugate representation
$h\in H,$
the conjugate representation
![]() $\sigma^h \in \widehat{N}_{\rm fd}$
is defined by
$\sigma^h \in \widehat{N}_{\rm fd}$
is defined by
![]() $\sigma^ h(n)=\sigma( h^{-1} n h)$
for all
$\sigma^ h(n)=\sigma( h^{-1} n h)$
for all
![]() $n\in N.$
$n\in N.$
Define
![]() $\widehat{N}_{ \rm fd}^{H-{\rm per}}$
as the set of
$\widehat{N}_{ \rm fd}^{H-{\rm per}}$
as the set of
![]() $\sigma\in \widehat{N}_{ \rm fd}$
with finite H-orbit.
$\sigma\in \widehat{N}_{ \rm fd}$
with finite H-orbit.
Observe that, due to the universal property of
![]() ${\rm Bohr}(N)$
, the group H acts by automorphisms on
${\rm Bohr}(N)$
, the group H acts by automorphisms on
![]() ${\rm Bohr}(N)$
. However, this action does not extend in general to an action of
${\rm Bohr}(N)$
. However, this action does not extend in general to an action of
![]() ${\rm Bohr}(H)$
on
${\rm Bohr}(H)$
on
![]() ${\rm Bohr}(N).$
${\rm Bohr}(N).$
Our first result shows that
![]() ${\rm Bohr}(G)$
is a split extension of
${\rm Bohr}(G)$
is a split extension of
![]() ${\rm Bohr}(H)$
by an appropriate quotient of
${\rm Bohr}(H)$
by an appropriate quotient of
![]() ${\rm Bohr}(N).$
${\rm Bohr}(N).$
Theorem A.
Let
![]() $G=N\rtimes H$
be a semi-direct product of locally compact groups. Let
$G=N\rtimes H$
be a semi-direct product of locally compact groups. Let
![]() $\varphi_N\,:\, {\rm Bohr}(N)\to \overline{\beta_G(N)}$
and
$\varphi_N\,:\, {\rm Bohr}(N)\to \overline{\beta_G(N)}$
and
![]() $\varphi_H\,:\, {\rm Bohr}(H)\to \overline{\beta_G(H)}$
be the maps such that
$\varphi_H\,:\, {\rm Bohr}(H)\to \overline{\beta_G(H)}$
be the maps such that
![]() $\varphi_N\circ \beta_N= \beta_G|_N$
and
$\varphi_N\circ \beta_N= \beta_G|_N$
and
![]() $\varphi_H\circ \beta_H= \beta_G|_H$
Set
$\varphi_H\circ \beta_H= \beta_G|_H$
Set
 \begin{equation*}C\,:\!=\,\bigcap_{\sigma \in \widehat{N}_{ \rm fd}^{H-{\rm per}}} {\rm {Ker}} ({\rm Bohr}(\sigma)).\end{equation*}
\begin{equation*}C\,:\!=\,\bigcap_{\sigma \in \widehat{N}_{ \rm fd}^{H-{\rm per}}} {\rm {Ker}} ({\rm Bohr}(\sigma)).\end{equation*}
-
(i) We have
 ${\rm {Ker}} \varphi_N =C$
and so
${\rm {Ker}} \varphi_N =C$
and so
 $\varphi_N$
induces a topological isomorphism
$\varphi_N$
induces a topological isomorphism
 $\overline{\varphi_N}\,:\, {\rm Bohr}(N)/C \to \overline{\beta_G(N)}.$
$\overline{\varphi_N}\,:\, {\rm Bohr}(N)/C \to \overline{\beta_G(N)}.$
-
(ii)
 $\varphi_H\,:\, {\rm Bohr}(H)\to \overline{\beta_G(H)}$
is a topological isomorphism.
$\varphi_H\,:\, {\rm Bohr}(H)\to \overline{\beta_G(H)}$
is a topological isomorphism.
-
(iii) The action of H by automorphisms on
 ${\rm Bohr}(N)$
induces an action of
${\rm Bohr}(N)$
induces an action of
 ${\rm Bohr}(H)$
by automorphisms on
${\rm Bohr}(H)$
by automorphisms on
 ${\rm Bohr}(N)/C$
and the maps
${\rm Bohr}(N)/C$
and the maps
 $\overline{\varphi_N}$
and
$\overline{\varphi_N}$
and
 $\varphi_H$
give rise to an isomorphism
$\varphi_H$
give rise to an isomorphism
 \begin{equation*} {\rm Bohr}(G)\cong ({\rm Bohr}(N)/C) \rtimes {\rm Bohr}(H).\end{equation*}
\begin{equation*} {\rm Bohr}(G)\cong ({\rm Bohr}(N)/C) \rtimes {\rm Bohr}(H).\end{equation*}
We turn to the description of
![]() ${\rm Prof}(G).$
Let
${\rm Prof}(G).$
Let
![]() $\widehat{N}_{ \rm finite} $
be the set of equivalence classes of irreducible unitary representations
$\widehat{N}_{ \rm finite} $
be the set of equivalence classes of irreducible unitary representations
![]() $\sigma$
of N with finite image
$\sigma$
of N with finite image
![]() $\sigma(N).$
Observe that the action of H on
$\sigma(N).$
Observe that the action of H on
![]() $ \widehat{N}_{\rm fd}$
preserves
$ \widehat{N}_{\rm fd}$
preserves
![]() $\widehat{N}_{ \rm finite}.$
Let
$\widehat{N}_{ \rm finite}.$
Let
![]() $\widehat{N}_{ \rm finite}^{H-{\rm per}}$
be the subset of
$\widehat{N}_{ \rm finite}^{H-{\rm per}}$
be the subset of
![]() $\widehat{N}_{ \rm finite}$
of representations with finite H-orbit. Every
$\widehat{N}_{ \rm finite}$
of representations with finite H-orbit. Every
![]() $\sigma\in \widehat{N}_{ \rm finite}$
gives rise to the unitary representation
$\sigma\in \widehat{N}_{ \rm finite}$
gives rise to the unitary representation
![]() ${\rm Prof}({\sigma}) $
of
${\rm Prof}({\sigma}) $
of
![]() ${\rm Prof}(N)$
.
${\rm Prof}(N)$
.
A result completely similar to Theorem A holds for
![]() ${\rm Prof}(G)$
.
${\rm Prof}(G)$
.
Theorem B.
Let
![]() $G=N\rtimes H$
be a semi-direct product of locally compact groups. Let
$G=N\rtimes H$
be a semi-direct product of locally compact groups. Let
![]() $\psi_N\,:\, {\rm Prof}(N)\to \overline{\alpha_G(N)}$
and
$\psi_N\,:\, {\rm Prof}(N)\to \overline{\alpha_G(N)}$
and
![]() $\psi_H\,:\, {\rm Prof}(H)\to \overline{\alpha_G(H)}$
be the maps such that
$\psi_H\,:\, {\rm Prof}(H)\to \overline{\alpha_G(H)}$
be the maps such that
![]() $\psi_N\circ \alpha_N= \alpha_G|_N$
and
$\psi_N\circ \alpha_N= \alpha_G|_N$
and
![]() $\psi_H\circ \alpha_H= \alpha_G|_H$
Set
$\psi_H\circ \alpha_H= \alpha_G|_H$
Set
 \begin{equation*}D\,:\!=\,\bigcap_{\sigma \in \widehat{N}_{ \rm finite}^{H-{\rm per}}} {\rm {Ker}} ({\rm Prof}({\sigma})).\end{equation*}
\begin{equation*}D\,:\!=\,\bigcap_{\sigma \in \widehat{N}_{ \rm finite}^{H-{\rm per}}} {\rm {Ker}} ({\rm Prof}({\sigma})).\end{equation*}
-
(i) We have
 ${\rm {Ker}} \psi_N =D$
and so
${\rm {Ker}} \psi_N =D$
and so
 $\psi_N$
induces a topological isomorphism
$\psi_N$
induces a topological isomorphism
 $\overline{\psi_N}\,:\, {\rm Prof}(N)/D \to \overline{\alpha_G(N)}.$
$\overline{\psi_N}\,:\, {\rm Prof}(N)/D \to \overline{\alpha_G(N)}.$
-
(ii)
 $\psi_H\,:\, {\rm Prof}(H)\to \overline{\alpha_G(H)}$
is a topological isomorphism.
$\psi_H\,:\, {\rm Prof}(H)\to \overline{\alpha_G(H)}$
is a topological isomorphism.
-
(iii) The action of H by automorphisms on
 ${\rm Prof}(N)$
induces an action of
${\rm Prof}(N)$
induces an action of
 ${\rm Prof}(H)$
by automorphisms on
${\rm Prof}(H)$
by automorphisms on
 ${\rm Prof}(N)/D$
and the maps
${\rm Prof}(N)/D$
and the maps
 $\overline{\psi_N}$
and
$\overline{\psi_N}$
and
 $\psi_H$
give rise to an isomorphism
$\psi_H$
give rise to an isomorphism
 \begin{equation*}{\rm Prof}(G) \cong ({\rm Prof}(N)/D) \rtimes {\rm Prof}(H) .\end{equation*}
\begin{equation*}{\rm Prof}(G) \cong ({\rm Prof}(N)/D) \rtimes {\rm Prof}(H) .\end{equation*}
When N is a finitely generated (discrete) group, we obtain the following well known result (see [ Reference Grunewald and ZalesskiiGZ11 , proposition 2·6]).
Corollary C.
Assume that N is finitely generated. Then
![]() ${\rm Prof}(G) \cong {\rm Prof}(N) \rtimes {\rm Prof}(H) .$
${\rm Prof}(G) \cong {\rm Prof}(N) \rtimes {\rm Prof}(H) .$
In the case where N is abelian, we can give a more explicit description of the quotients
![]() ${\rm Bohr}(N)/C$
and
${\rm Bohr}(N)/C$
and
![]() ${\rm Prof}(N)/D$
appearing in Theorems A and B. Recall that, in this case, the dual group
${\rm Prof}(N)/D$
appearing in Theorems A and B. Recall that, in this case, the dual group
![]() $\widehat{N}$
is the group of continuous homomorphisms from N to the circle group
$\widehat{N}$
is the group of continuous homomorphisms from N to the circle group
![]() $\textbf{S}^1$
. We will also consider the subgroup
$\textbf{S}^1$
. We will also consider the subgroup
![]() $\widehat{N}_{\rm fin}$
of
$\widehat{N}_{\rm fin}$
of
![]() $\chi\in \widehat{N}$
with finite image
$\chi\in \widehat{N}$
with finite image
![]() $\chi(N)$
, that is, with values in the subgroup of m-th roots of unity in
$\chi(N)$
, that is, with values in the subgroup of m-th roots of unity in
![]() $\textbf{C}$
for some integer
$\textbf{C}$
for some integer
![]() $m\geq 1.$
Observe also that
$m\geq 1.$
Observe also that
![]() $\widehat{N}^{H-{\rm per}}$
and
$\widehat{N}^{H-{\rm per}}$
and
![]() $\widehat{N}_{ \rm finite}^{H-{\rm per}}$
are subgroups of
$\widehat{N}_{ \rm finite}^{H-{\rm per}}$
are subgroups of
![]() $\widehat{N}$
.
$\widehat{N}$
.
Corollary D.
Assume that N is an abelian locally compact group. Let
![]() $\widehat{N}^{H-{\rm per}}$
and
$\widehat{N}^{H-{\rm per}}$
and
![]() $\widehat{N}_{ \rm finite}^{H-{\rm per}}$
be equipped with the discrete topology. Let A and B be their respective dual groups. Then
$\widehat{N}_{ \rm finite}^{H-{\rm per}}$
be equipped with the discrete topology. Let A and B be their respective dual groups. Then
Recall that G is maximally almost periodic, or MAP, if
![]() $\widehat{G}_{ \rm fd}$
separates its points (equivalently, if
$\widehat{G}_{ \rm fd}$
separates its points (equivalently, if
![]() $\beta_G\,:\, G\to {\rm Bohr}(G)$
is injective); recall also that G is residually finite, or RF, if
$\beta_G\,:\, G\to {\rm Bohr}(G)$
is injective); recall also that G is residually finite, or RF, if
![]() $\widehat{G}_{ \rm finite}$
separates its points (equivalently, if
$\widehat{G}_{ \rm finite}$
separates its points (equivalently, if
![]() $\alpha_G\,:\, G\to {\rm Prof}(G)$
is injective).
$\alpha_G\,:\, G\to {\rm Prof}(G)$
is injective).
Corollary E.
Let
![]() $G=N\rtimes H$
be a semi-direct product of locally compact groups.
$G=N\rtimes H$
be a semi-direct product of locally compact groups.
-
(i) G is MAP if and only if H is MAP and
 $\widehat{N}_{ \rm fd}^{H-{\rm per}}$
separates the points of N.
$\widehat{N}_{ \rm fd}^{H-{\rm per}}$
separates the points of N.
-
(ii) G is RF if and only if H is RF and
 $\widehat{N}_{ \rm finite}^{H-{\rm per}}$
separates the points of N.
$\widehat{N}_{ \rm finite}^{H-{\rm per}}$
separates the points of N.
We give an application of our results to wreath products. Let
![]() $H, \Lambda$
be groups, X a non empty set, and
$H, \Lambda$
be groups, X a non empty set, and
![]() $H \curvearrowright X$
an action of H on X. Then H acts on the direct sum
$H \curvearrowright X$
an action of H on X. Then H acts on the direct sum
![]() $\oplus_{x\in X} \Lambda,$
by shifting the indices. The (permutational) wreath product, denoted
$\oplus_{x\in X} \Lambda,$
by shifting the indices. The (permutational) wreath product, denoted
![]() $\Lambda\wr_{X} H,$
is the semidirect product
$\Lambda\wr_{X} H,$
is the semidirect product
When the action of H on X is simply transitive, we obtain the standard wreath product denoted
![]() $\Lambda\wr H.$
Observe that
$\Lambda\wr H.$
Observe that
![]() $\Lambda^{\rm Ab}\wr_X H$
is a quotient of
$\Lambda^{\rm Ab}\wr_X H$
is a quotient of
![]() $\Lambda\wr_X H,$
where
$\Lambda\wr_X H,$
where
![]() $\Lambda^{\rm Ab}$
is the abelianization
$\Lambda^{\rm Ab}$
is the abelianization
![]() $\Lambda/[\Lambda, \Lambda]$
of
$\Lambda/[\Lambda, \Lambda]$
of
![]() $\Lambda.$
$\Lambda.$
Initially, we formulated the next two corollaries only for standard wreath products; the extension of these results to more general wreath products was suggested to us by the referee.
Corollary F.
Let
![]() $H, \Lambda$
be groups, and let
$H, \Lambda$
be groups, and let
![]() $H \curvearrowright X$
be a transitive action of H on a set X. Let
$H \curvearrowright X$
be a transitive action of H on a set X. Let
![]() $\Lambda\wr_{X} H$
be equipped with the discrete topology.
$\Lambda\wr_{X} H$
be equipped with the discrete topology.
-
(i) When X is finite, we have
 \[\begin{aligned}&{\rm Bohr}(\Lambda\wr_X H)\cong \left( \oplus_{x\in X}{\rm Bohr}(\Lambda)\right) \rtimes {\rm Bohr}(H) \ \text{and}\\&{\rm Prof}(\Lambda\wr_X H)\cong \left( \oplus_{x\in X}{\rm Prof}(\Lambda)\right) \rtimes {\rm Prof}(H).\end{aligned}\]
\[\begin{aligned}&{\rm Bohr}(\Lambda\wr_X H)\cong \left( \oplus_{x\in X}{\rm Bohr}(\Lambda)\right) \rtimes {\rm Bohr}(H) \ \text{and}\\&{\rm Prof}(\Lambda\wr_X H)\cong \left( \oplus_{x\in X}{\rm Prof}(\Lambda)\right) \rtimes {\rm Prof}(H).\end{aligned}\]
-
(ii) When X is infinite, the quotient map
 $\Lambda\wr_X H\to \Lambda^{\rm Ab}\wr_X H$
induces isomorphisms In particular, if
$\Lambda\wr_X H\to \Lambda^{\rm Ab}\wr_X H$
induces isomorphisms In particular, if \begin{equation*}{\rm Bohr}(\Lambda\wr_X H)\cong {\rm Bohr}( \Lambda^{\rm Ab}\wr_X H) \ \text{and}\ {\rm Prof}(\Lambda\wr_X H)\cong {\rm Prof}( \Lambda^{\rm Ab}\wr_X H)\end{equation*}
\begin{equation*}{\rm Bohr}(\Lambda\wr_X H)\cong {\rm Bohr}( \Lambda^{\rm Ab}\wr_X H) \ \text{and}\ {\rm Prof}(\Lambda\wr_X H)\cong {\rm Prof}( \Lambda^{\rm Ab}\wr_X H)\end{equation*}
 $\Lambda$
is perfect (that is,
$\Lambda$
is perfect (that is,
 $\Lambda=[\Lambda, \Lambda]$
), the quotient map
$\Lambda=[\Lambda, \Lambda]$
), the quotient map
 $\Lambda\wr_X H\to H$
induces isomorphisms
$\Lambda\wr_X H\to H$
induces isomorphisms  \begin{equation*}{\rm Bohr}(\Lambda\wr_X H)\cong {\rm Bohr}(H) \ \text{and}\ {\rm Prof}(\Lambda\wr_X H)\cong {\rm Prof}( H).\end{equation*}
\begin{equation*}{\rm Bohr}(\Lambda\wr_X H)\cong {\rm Bohr}(H) \ \text{and}\ {\rm Prof}(\Lambda\wr_X H)\cong {\rm Prof}( H).\end{equation*}
The following definition was suggested to us by the referee.
Definition 1. An action
![]() $H \curvearrowright X$
of a group H on a set X is residually finite or RF, if, for any pair
$H \curvearrowright X$
of a group H on a set X is residually finite or RF, if, for any pair
![]() $x_1, x_2$
of distinct elements of X, there exists a finite index subgroup L of H such that
$x_1, x_2$
of distinct elements of X, there exists a finite index subgroup L of H such that
![]() $L x_1\neq L x_2.$
$L x_1\neq L x_2.$
Observe that
![]() $H \curvearrowright X$
is RF if and only if
$H \curvearrowright X$
is RF if and only if
![]() $H \curvearrowright Y$
is RF for every H-orbit
$H \curvearrowright Y$
is RF for every H-orbit
![]() $Y\subset X.$
Observe also that, when
$Y\subset X.$
Observe also that, when
![]() $H \curvearrowright X$
is simply transitive, the action
$H \curvearrowright X$
is simply transitive, the action
![]() $H \curvearrowright X$
is RF if and only if the group H is RF.
$H \curvearrowright X$
is RF if and only if the group H is RF.
Item (ii) of the following result was proved, with different methods, in [ Reference GruenbergGru57 , theorem 3·2] for standard wreath products and in [ Reference CornulierCor14 , proposition 1·7] for permutational wreath products.
Corollary G.
Let
![]() $\Lambda, H$
be groups, and let
$\Lambda, H$
be groups, and let
![]() $H \curvearrowright X$
be an action of H on a set X. Let
$H \curvearrowright X$
be an action of H on a set X. Let
![]() $\Lambda\wr_{X} H$
be equipped with the discrete topology.
$\Lambda\wr_{X} H$
be equipped with the discrete topology.
Assume that
![]() $\Lambda$
has at least two elements.
$\Lambda$
has at least two elements.
-
(i) The group
 $\Lambda\wr_X H$
is MAP if and only if
$\Lambda\wr_X H$
is MAP if and only if
 $\Lambda$
and H are MAP, and either
$\Lambda$
and H are MAP, and either
-
–
 $\Lambda$
is abelian and
$\Lambda$
is abelian and
 $H \curvearrowright X$
is RF, or
$H \curvearrowright X$
is RF, or
-
– X is finite.
-
-
(ii) ([ Reference GruenbergGru57 ], [ Reference CornulierCor14 ]) The group
 $\Lambda\wr_X H$
is RF if and only if
$\Lambda\wr_X H$
is RF if and only if
 $\Lambda$
and H are RF, and either
$\Lambda$
and H are RF, and either-
–
 $\Lambda$
is abelian and
$\Lambda$
is abelian and
 $H \curvearrowright X$
is RF, or
$H \curvearrowright X$
is RF, or -
– X is finite.
-
Remark 2.
-
(i) The Bohr compactification of an abelian locally compact group A is easy to describe:
 ${\rm Bohr}(A)$
can be identified with
${\rm Bohr}(A)$
can be identified with
 $\widehat{\Gamma},$
where
$\widehat{\Gamma},$
where
 $\Gamma= \widehat{A}$
is viewed as discrete group; in case A is finitely generated, a more precise description of
$\Gamma= \widehat{A}$
is viewed as discrete group; in case A is finitely generated, a more precise description of
 ${\rm Bohr}(A)$
is available (see [
Reference BekkaBek23
, proposition 11]).
${\rm Bohr}(A)$
is available (see [
Reference BekkaBek23
, proposition 11]). -
(ii) Provided
 ${\rm Bohr}(H)$
and
${\rm Bohr}(H)$
and
 ${\rm Prof}(H)$
are known, Corollary F together with Corollary D give, in view of (i), a complete description of the Bohr compactification and the profinite completion of any wreath product
${\rm Prof}(H)$
are known, Corollary F together with Corollary D give, in view of (i), a complete description of the Bohr compactification and the profinite completion of any wreath product
 $\Lambda\wr_X H$
in case X is infinite.
$\Lambda\wr_X H$
in case X is infinite. -
(iii) Bohr compactifications of group and semigroup extensions have been studied by several authors, in a more abstract and less explicit setting ([ Reference Dangello and LindahlDL83 , Reference Junghenn and LernerJL81 , Reference JunghennJun78 , Reference Junghenn and MilnesJM02 , Reference LandstadLan72 , Reference MilnesMil83 ]); profinite completions of group extensions appear at numerous places in the literature ([ Reference Grunewald and ZalesskiiGZ11 , Reference Ribes and ZalesskiiRZ00 ]).
This paper is organised as follows. Section 2 contains some general facts about Bohr compactifications and profinite completions as well as some reminders on projective representations. In Section 3, we give the proof of Theorems A and B. Section 4 contains the proof of the corollaries. Section 5 is devoted to the explicit computation of the Bohr compactification and profinite completions for two groups: the lamplighter group
![]() $(\textbf{Z}/n\textbf{Z}) \wr \textbf{Z}$
and the Heisenberg group H(R) over an arbitrary commutative ring R.
$(\textbf{Z}/n\textbf{Z}) \wr \textbf{Z}$
and the Heisenberg group H(R) over an arbitrary commutative ring R.
2. Preliminaries
2·1. Models for Bohr compactifications and profinite completions
Let G be a topological group. We give well known models for
![]() ${\rm Bohr}(G)$
and
${\rm Bohr}(G)$
and
![]() ${\rm Prof}(G).$
For this, we use finite dimensional unitary representations of G, that is, continuous homomorphisms
${\rm Prof}(G).$
For this, we use finite dimensional unitary representations of G, that is, continuous homomorphisms
![]() $\pi\,:\, G\to U(n)$
for some integer
$\pi\,:\, G\to U(n)$
for some integer
![]() $n\geq 1.$
We denote by
$n\geq 1.$
We denote by
![]() $\widehat{G}_{\rm fd}$
the set of equivalence classes of irreducible finite dimensional unitary representations of G. Let
$\widehat{G}_{\rm fd}$
the set of equivalence classes of irreducible finite dimensional unitary representations of G. Let
![]() $\widehat{G}_{\rm finite}$
be the subset of
$\widehat{G}_{\rm finite}$
be the subset of
![]() $\widehat{G}_{\rm fd}$
consisting of representations
$\widehat{G}_{\rm fd}$
consisting of representations
![]() $\pi$
with finite image
$\pi$
with finite image
![]() $\pi(G).$
$\pi(G).$
For a compact (respectively, profinite) group K, the set
![]() $\widehat{K}_{\rm fd}$
(respectively,
$\widehat{K}_{\rm fd}$
(respectively,
![]() $\widehat{K}_{\rm finite}$
) coincides with the dual space
$\widehat{K}_{\rm finite}$
) coincides with the dual space
![]() $\widehat{K}$
, that is, the set of equivalence classes of unitary representations of K.
$\widehat{K}$
, that is, the set of equivalence classes of unitary representations of K.
A useful tool for the identification of
![]() ${\rm Bohr}(G)$
or
${\rm Bohr}(G)$
or
![]() ${\rm Prof}(G)$
is given by the following proposition; for the easy proof, see [
Reference BekkaBek23
, propositions 5 and 6].
${\rm Prof}(G)$
is given by the following proposition; for the easy proof, see [
Reference BekkaBek23
, propositions 5 and 6].
Proposition 3
-
(i) Let K be a compact group and
 $\beta\,:\, G\to K$
a continuous homomorphism with dense image; then
$\beta\,:\, G\to K$
a continuous homomorphism with dense image; then
 $(K, \beta)$
is a Bohr compactification of G if and only if the map
$(K, \beta)$
is a Bohr compactification of G if and only if the map
 $\widehat{\beta}\,:\,\widehat{K}\to \widehat{G}_{\rm fd},$
given by
$\widehat{\beta}\,:\,\widehat{K}\to \widehat{G}_{\rm fd},$
given by
 $\widehat{\beta}(\pi)= \pi\circ \beta,$
is surjective.
$\widehat{\beta}(\pi)= \pi\circ \beta,$
is surjective.
-
(ii) Let L a be profinite group and
 $\alpha\,:\, G\to L$
a continuous homomorphism with dense image; then
$\alpha\,:\, G\to L$
a continuous homomorphism with dense image; then
 $(L, \alpha)$
is a profinite completion of G if and only if the map
$(L, \alpha)$
is a profinite completion of G if and only if the map
 $\widehat{\beta}\,:\,\widehat{L}\to \widehat{G}_{\rm finite},$
given by
$\widehat{\beta}\,:\,\widehat{L}\to \widehat{G}_{\rm finite},$
given by
 $\widehat{\beta}(\pi)= \pi\circ \beta,$
is surjective.
$\widehat{\beta}(\pi)= \pi\circ \beta,$
is surjective.
The following proposition is an immediate consequence of Proposition 3.
Proposition 4. Choose families
of representatives for the sets
![]() $\widehat{G}_{\rm fd}$
and
$\widehat{G}_{\rm fd}$
and
![]() $\widehat{G}_{\rm finite},$
respectively.
$\widehat{G}_{\rm finite},$
respectively.
-
(i) Let
 $\beta\,:\, G \to \prod_{i \in I} U(n_i)$
be given by
$\beta\,:\, G \to \prod_{i \in I} U(n_i)$
be given by
 $\beta(g)= \bigoplus_{i \in I} \pi_i(g) $
and let K be the closure of
$\beta(g)= \bigoplus_{i \in I} \pi_i(g) $
and let K be the closure of
 $\beta(G)$
. Then
$\beta(G)$
. Then
 $(K, \beta)$
is a Bohr compactification of G.
$(K, \beta)$
is a Bohr compactification of G.
-
(ii) Let
 $\alpha\,:\, G \to \prod_{j \in J} U(n_j)$
be given by
$\alpha\,:\, G \to \prod_{j \in J} U(n_j)$
be given by
 $\alpha(g)= \bigoplus_{j \in J} \sigma_j(g) $
and let L be the closure of
$\alpha(g)= \bigoplus_{j \in J} \sigma_j(g) $
and let L be the closure of
 $\alpha(G)$
. Then
$\alpha(G)$
. Then
 $(L, \alpha)$
is a profinite completion of G.
$(L, \alpha)$
is a profinite completion of G.
We observe that a more common model for the profinite completion of G is the projective limit
![]() $\varprojlim G/H$
, where H runs over the family of the normal subgroups of finite index of G, together with the natural homomorphism
$\varprojlim G/H$
, where H runs over the family of the normal subgroups of finite index of G, together with the natural homomorphism
![]() $G \to \varprojlim G/H$
(see e.g. [
Reference Ribes and ZalesskiiRZ00
, 2·1·6])
$G \to \varprojlim G/H$
(see e.g. [
Reference Ribes and ZalesskiiRZ00
, 2·1·6])
2·2. Extension of representations
We will also use the notion of a projective representation. Let G be a locally compact group. A map
![]() $\pi\,:\, G \to U(n)$
is a projective representation of G if the following holds:
$\pi\,:\, G \to U(n)$
is a projective representation of G if the following holds:
![]() $\pi(e)=I$
,
$\pi(e)=I$
,
for all
![]() $g_1,g_2\in G,$
there exists
$g_1,g_2\in G,$
there exists
![]() $c(g_1 , g_2 )\in \textbf{S}^1 $
such that
$c(g_1 , g_2 )\in \textbf{S}^1 $
such that
![]() $\pi$
is Borel measurable.
$\pi$
is Borel measurable.
The map
![]() $c\,:\,G \times G \to \textbf{S}^1$
is a 2-cocycle with values in the unit circle
$c\,:\,G \times G \to \textbf{S}^1$
is a 2-cocycle with values in the unit circle
![]() $\textbf{S}^1.$
The conjugate representation
$\textbf{S}^1.$
The conjugate representation
![]() $\overline{\pi}\,:\, G\to U(n)$
is another projective representation defined by
$\overline{\pi}\,:\, G\to U(n)$
is another projective representation defined by
![]() $\overline{\pi}(g)= J\pi(g) J,$
where
$\overline{\pi}(g)= J\pi(g) J,$
where
![]() $J\,:\, \textbf{C}^n\to \textbf{C}^n$
is the anti-linear map given by conjugation of the coordinates,
$J\,:\, \textbf{C}^n\to \textbf{C}^n$
is the anti-linear map given by conjugation of the coordinates,
The proof of the following lemma is straightforward.
Lemma 5.
Let
![]() $\pi\,:\, G\to U(n)$
be a projective representation of G, with associated cocycle
$\pi\,:\, G\to U(n)$
be a projective representation of G, with associated cocycle
![]() $c\,:\,G \times G \to \textbf{S}^1$
. Let
$c\,:\,G \times G \to \textbf{S}^1$
. Let
![]() $\pi'\,:\, G\to U(m)$
be another projective representation of G with associated cocycle 2-cocycle
$\pi'\,:\, G\to U(m)$
be another projective representation of G with associated cocycle 2-cocycle
![]() $c'\,:\,G \times G \to \textbf{S}^1$
.
$c'\,:\,G \times G \to \textbf{S}^1$
.
-
(i)
 $\overline{\pi}\,:\, G\to U(n)$
is a projective representation of G with
$\overline{\pi}\,:\, G\to U(n)$
is a projective representation of G with
 $\overline{c}$
as associated cocycle.
$\overline{c}$
as associated cocycle.
-
(ii) The tensor product
is a projective representation of G with cc’ as associated cocycle. \begin{equation*}\pi\otimes \pi'\,:\, G\to U(nm), \qquad g\mapsto \pi(g)\otimes \pi'(g)\end{equation*}
\begin{equation*}\pi\otimes \pi'\,:\, G\to U(nm), \qquad g\mapsto \pi(g)\otimes \pi'(g)\end{equation*}
Let N be a closed normal subgroup of G. Recall that the stabiliser
![]() ${G}_\pi$
in G of an irreducible unitary representation
${G}_\pi$
in G of an irreducible unitary representation
![]() $\pi$
of N is the set of
$\pi$
of N is the set of
![]() $g\in G$
such that
$g\in G$
such that
![]() $\pi^g$
is equivalent to
$\pi^g$
is equivalent to
![]() $\pi.$
Observe that
$\pi.$
Observe that
![]() $G_\pi$
contains N.
$G_\pi$
contains N.
The following proposition is a well known fact from the Clifford–Mackey theory of unitary representations of group extensions (see [ Reference Curtis and ReinerCR62 , chapter 1, section 11] and [ Reference MackeyMac58 ]).
Proposition 6.
Let
![]() $G= N\rtimes H$
be the semi-direct product of the locally compact groups H and N. Let
$G= N\rtimes H$
be the semi-direct product of the locally compact groups H and N. Let
![]() $\pi\,:\, N\to U(m)$
be an irreducible unitary representation of N and assume that
$\pi\,:\, N\to U(m)$
be an irreducible unitary representation of N and assume that
![]() $G= G_\pi.$
There exists a projective representation
$G= G_\pi.$
There exists a projective representation
![]() $\widetilde\pi\,:\, G\to U(m)$
with the following properties:
$\widetilde\pi\,:\, G\to U(m)$
with the following properties:
-
(i)
 $\widetilde\pi$
extends
$\widetilde\pi$
extends
 $\pi$
, that is,
$\pi$
, that is,
 $\widetilde\pi(n)= \pi(n)$
for every
$\widetilde\pi(n)= \pi(n)$
for every
 $n\in N;$
$n\in N;$
-
(ii) the 2-cocycle
 $\widetilde{c}\,:\,G \times G\to \textbf{S}^1$
associated to
$\widetilde{c}\,:\,G \times G\to \textbf{S}^1$
associated to
 $\widetilde\pi$
has the form
$\widetilde\pi$
has the form
 $\widetilde{c}=c\circ (p\times p),$
for a map
$\widetilde{c}=c\circ (p\times p),$
for a map
 $c\,:\, H\times H\to \textbf{S}^1$
, where
$c\,:\, H\times H\to \textbf{S}^1$
, where
 $p\,:\, G \to H$
is the canonical homomorphism.
$p\,:\, G \to H$
is the canonical homomorphism.
Proof. Let
![]() $S\subset U(m)$
be a Borel transversal for the quotient space
$S\subset U(m)$
be a Borel transversal for the quotient space
![]() $PU(m)= U(m)/\textbf{S}^1$
with
$PU(m)= U(m)/\textbf{S}^1$
with
![]() $I_m\in S.$
Let
$I_m\in S.$
Let
![]() $h\in H$
. Since
$h\in H$
. Since
![]() $G=G_\pi$
and since
$G=G_\pi$
and since
![]() $\pi$
is irreducible, there exists a unique matrix
$\pi$
is irreducible, there exists a unique matrix
![]() $\widetilde\pi(h)\in S$
such that
$\widetilde\pi(h)\in S$
such that
Define
![]() $\widetilde\pi\,:\, G\to U(n)$
by
$\widetilde\pi\,:\, G\to U(n)$
by
It is clear that
![]() $\widetilde{\pi}|_N= \pi$
and that
$\widetilde{\pi}|_N= \pi$
and that
It can be shown (see [
Reference MackeyMac58
, proof of theorem 8·2]) that
![]() $\widetilde{\pi}$
is a measurable map.
$\widetilde{\pi}$
is a measurable map.
Let
![]() $g_1,g_2\in G$
. For every
$g_1,g_2\in G$
. For every
![]() $n\in N,$
we have, on the one hand,
$n\in N,$
we have, on the one hand,
and on the other hand
 \[\begin{aligned}\pi (g_1g_2n g_2^{-1}g_1)&= \widetilde\pi(g_1) \pi(g_2 n g_2^{-1}) \widetilde\pi(g_1)^{-1}\\&=\widetilde\pi(g_1) \widetilde\pi(g_2)\pi(n)\widetilde\pi (g_1)^{-1} \widetilde\pi (g_2)^{-1}.\end{aligned}\]
\[\begin{aligned}\pi (g_1g_2n g_2^{-1}g_1)&= \widetilde\pi(g_1) \pi(g_2 n g_2^{-1}) \widetilde\pi(g_1)^{-1}\\&=\widetilde\pi(g_1) \widetilde\pi(g_2)\pi(n)\widetilde\pi (g_1)^{-1} \widetilde\pi (g_2)^{-1}.\end{aligned}\]
Since
![]() $\pi$
is irreducible, it follows that
$\pi$
is irreducible, it follows that
for some scalar
![]() $\widetilde{c}(g_1, g_2)\in \textbf{S}^1$
.
$\widetilde{c}(g_1, g_2)\in \textbf{S}^1$
.
Moreover, for
![]() $g_1= n_1h_1, g_2= n_2 h_2,$
we have, on the one hand,
$g_1= n_1h_1, g_2= n_2 h_2,$
we have, on the one hand,
and, on the other hand,
 \[ \begin{aligned} \widetilde\pi(g_1 g_2)&=\widetilde\pi(n_1(h_1n_2 h_1^{-1}) h_1h_2)\\ & =\pi(n_1(h_1n_2 h_1^{-1})) \widetilde \pi(h_1h_2)\\ &=\pi(n_1) \pi(h_1n_2 h_1^{-1}) \widetilde \pi(h_1h_2)\\ &=\pi(n_1) \widetilde\pi(h_1) \pi(n_2) \widetilde\pi(h_1)^{-1} \widetilde \pi(h_1h_2)\\ &=\widetilde{c}(h_1, h_2) \pi(n_1) \widetilde\pi(h_1) \pi(n_2) \widetilde\pi(h_1)^{-1} \widetilde \pi(h_1)\widetilde \pi(h_2)\\ &=\widetilde{c}(h_1, h_2)\pi(n_1) \widetilde\pi(h_1) \pi(n_2)\widetilde \pi(h_2); \end{aligned} \]
\[ \begin{aligned} \widetilde\pi(g_1 g_2)&=\widetilde\pi(n_1(h_1n_2 h_1^{-1}) h_1h_2)\\ & =\pi(n_1(h_1n_2 h_1^{-1})) \widetilde \pi(h_1h_2)\\ &=\pi(n_1) \pi(h_1n_2 h_1^{-1}) \widetilde \pi(h_1h_2)\\ &=\pi(n_1) \widetilde\pi(h_1) \pi(n_2) \widetilde\pi(h_1)^{-1} \widetilde \pi(h_1h_2)\\ &=\widetilde{c}(h_1, h_2) \pi(n_1) \widetilde\pi(h_1) \pi(n_2) \widetilde\pi(h_1)^{-1} \widetilde \pi(h_1)\widetilde \pi(h_2)\\ &=\widetilde{c}(h_1, h_2)\pi(n_1) \widetilde\pi(h_1) \pi(n_2)\widetilde \pi(h_2); \end{aligned} \]
this shows that
![]() $\widetilde{c}(n_1 h_1, n_2 h_2)=\widetilde{c}(h_1, h_2).$
$\widetilde{c}(n_1 h_1, n_2 h_2)=\widetilde{c}(h_1, h_2).$
2·3. Bohr compactification and profinite completion of quotients
Let G be a topological group and N a closed normal subgroup of G. Let
![]() $({\rm Bohr}(G), \beta_G)$
and
$({\rm Bohr}(G), \beta_G)$
and
![]() $({\rm Prof}(G), \alpha_G)$
be a Bohr compactification and a profinite completion of G. Let
$({\rm Prof}(G), \alpha_G)$
be a Bohr compactification and a profinite completion of G. Let
![]() ${\rm Bohr}(p)\,:\, {\rm Bohr}(G)\to {\rm Bohr}(G/N)$
and
${\rm Bohr}(p)\,:\, {\rm Bohr}(G)\to {\rm Bohr}(G/N)$
and
![]() ${\rm Prof}(p)\,:\, {\rm Bohr}(G)\to {\rm Bohr}(G/N)$
be the morphisms induced by the canonical epimorphism
${\rm Prof}(p)\,:\, {\rm Bohr}(G)\to {\rm Bohr}(G/N)$
be the morphisms induced by the canonical epimorphism
![]() $p\,:\, G\to G/N$
. The following proposition is well known (see [
Reference Hart and KunenHK01
, lemma 2·2] or [
Reference BekkaBek23
, proposition 10] for (i) and [
Reference Ribes and ZalesskiiRZ00
, proposition 3·2·5] for (ii)). For the convenience of the reader, we give for (ii) a proof which is different from the one in [
Reference Ribes and ZalesskiiRZ00
]
$p\,:\, G\to G/N$
. The following proposition is well known (see [
Reference Hart and KunenHK01
, lemma 2·2] or [
Reference BekkaBek23
, proposition 10] for (i) and [
Reference Ribes and ZalesskiiRZ00
, proposition 3·2·5] for (ii)). For the convenience of the reader, we give for (ii) a proof which is different from the one in [
Reference Ribes and ZalesskiiRZ00
]
Proposition 7
-
(i)
 $\mathrm{Bohr}(p)$
is surjective and its kernel is
$\mathrm{Bohr}(p)$
is surjective and its kernel is
 $\overline{\beta_G(N)}$
.
$\overline{\beta_G(N)}$
. -
(ii)
 $\mathrm{Prof}(p)$
is surjective and its kernel is
$\mathrm{Prof}(p)$
is surjective and its kernel is
 $\overline{\alpha_G(N)}$
.
$\overline{\alpha_G(N)}$
.
Proof. To show (ii), set
![]() $K\,:\!=\,\overline{\alpha_G(N)}$
. Let
$K\,:\!=\,\overline{\alpha_G(N)}$
. Let
![]() $({\rm Prof}(G/N),\overline{\alpha})$
be a profinite completion of
$({\rm Prof}(G/N),\overline{\alpha})$
be a profinite completion of
![]() $G/N.$
We have a commutative diagram
$G/N.$
We have a commutative diagram

It follows that
![]() $\alpha_G(N)$
and hence K is contained in
$\alpha_G(N)$
and hence K is contained in
![]() ${{\rm Ker}}({\rm Prof}(p)).$
So, we have induced homomorphisms
${{\rm Ker}}({\rm Prof}(p)).$
So, we have induced homomorphisms
![]() $\beta\,:\, G/N\to {\rm Prof}(G)/K$
and
$\beta\,:\, G/N\to {\rm Prof}(G)/K$
and
![]() $\beta'\,:\, {\rm Prof}(G)/K\to {\rm Prof}(G/N),$
giving rise to a commutative diagram
$\beta'\,:\, {\rm Prof}(G)/K\to {\rm Prof}(G/N),$
giving rise to a commutative diagram

It follows that
![]() $({\rm Prof}(G)/K, \beta)$
has the same universal property for
$({\rm Prof}(G)/K, \beta)$
has the same universal property for
![]() $G/N$
as
$G/N$
as
![]() $({\rm Prof}(G/N),\overline{\alpha})$
; it is therefore a profinite completion of
$({\rm Prof}(G/N),\overline{\alpha})$
; it is therefore a profinite completion of
![]() $G/N.$
$G/N.$
3. Proof of Theorems A and B
3·1. Proof of Theorem A
Set
![]() $K\,:\!=\, \overline{\beta_G(N)},$
where
$K\,:\!=\, \overline{\beta_G(N)},$
where
![]() $\beta_G$
is the canonical map from the locally compact group
$\beta_G$
is the canonical map from the locally compact group
![]() $G= N\rtimes H$
to
$G= N\rtimes H$
to
![]() ${\rm Bohr}(G).$
${\rm Bohr}(G).$
-
(i) First step. We claim that
 \begin{equation*} \left\{\widehat{\sigma}\circ (\beta_G|_N)\,:\, \widehat{\sigma} \in \widehat{K}\right\} \subset \widehat{N}_{ \rm fd}^{H-{\rm per}}. \end{equation*}
\begin{equation*} \left\{\widehat{\sigma}\circ (\beta_G|_N)\,:\, \widehat{\sigma} \in \widehat{K}\right\} \subset \widehat{N}_{ \rm fd}^{H-{\rm per}}. \end{equation*}
Indeed, let
![]() $\widehat{\sigma} \in \widehat{K}$
. Then
$\widehat{\sigma} \in \widehat{K}$
. Then
![]() $\sigma\,:\!=\, \widehat{\sigma}\circ (\beta_G|_N)\in \widehat{N}_{ \rm fd}.$
Let
$\sigma\,:\!=\, \widehat{\sigma}\circ (\beta_G|_N)\in \widehat{N}_{ \rm fd}.$
Let
![]() $ \widehat{\rho}\in \widehat{{\rm Bohr}(G)}$
be an irreducible subrepresentation of the induced representation
$ \widehat{\rho}\in \widehat{{\rm Bohr}(G)}$
be an irreducible subrepresentation of the induced representation
![]() ${\rm Ind}_{K}^{{\rm Bohr}(G)} \widehat{\sigma}.$
Then, by Frobenius reciprocity,
${\rm Ind}_{K}^{{\rm Bohr}(G)} \widehat{\sigma}.$
Then, by Frobenius reciprocity,
![]() $\widehat{\sigma}$
is equivalent to a subrepresentation of
$\widehat{\sigma}$
is equivalent to a subrepresentation of
![]() $\widehat{\rho}|_K.$
Hence,
$\widehat{\rho}|_K.$
Hence,
![]() $\sigma$
is equivalent to a subrepresentation of
$\sigma$
is equivalent to a subrepresentation of
![]() $(\widehat{\rho} \circ \beta_G)|N.$
The decomposition of the finite dimensional representation
$(\widehat{\rho} \circ \beta_G)|N.$
The decomposition of the finite dimensional representation
![]() $(\widehat{\rho} \circ \beta_G)|_N$
into isotypical components shows that
$(\widehat{\rho} \circ \beta_G)|_N$
into isotypical components shows that
![]() $\sigma$
has a finite H-orbit (see [
Reference BekkaBek23
, proposition 12]).
$\sigma$
has a finite H-orbit (see [
Reference BekkaBek23
, proposition 12]).
-
(ii) Second step. We claim that
 \begin{equation*} \widehat{N}_{ \rm fd}^{H-{\rm per}} \subset \left\{\widehat{\sigma} \circ (\beta_G|_N)\,:\, \widehat{\sigma} \in \widehat{K}\right\}. \end{equation*}
\begin{equation*} \widehat{N}_{ \rm fd}^{H-{\rm per}} \subset \left\{\widehat{\sigma} \circ (\beta_G|_N)\,:\, \widehat{\sigma} \in \widehat{K}\right\}. \end{equation*}
Indeed, let
![]() $\sigma\,:\, N\to U(m)$
be a representation of N with finite H-orbit. By Proposition 6, there exists a projective representation
$\sigma\,:\, N\to U(m)$
be a representation of N with finite H-orbit. By Proposition 6, there exists a projective representation
![]() $\widetilde{\sigma}$
of
$\widetilde{\sigma}$
of
![]() $G_\sigma=NH_\sigma$
which extends
$G_\sigma=NH_\sigma$
which extends
![]() $\sigma$
and the associated cocycle
$\sigma$
and the associated cocycle
![]() $c\,:\, G_\sigma\times G_\sigma\to \textbf{S}^1$
, factorises through
$c\,:\, G_\sigma\times G_\sigma\to \textbf{S}^1$
, factorises through
![]() $H_\sigma\times H_\sigma$
.
$H_\sigma\times H_\sigma$
.
Define a projective representation
![]() $\tau\,:\, G_\sigma\to U(m)$
of
$\tau\,:\, G_\sigma\to U(m)$
of
![]() $G_\sigma$
by
$G_\sigma$
by
Observe that
![]() $\tau$
is trivial on N and that its associated cocycle is
$\tau$
is trivial on N and that its associated cocycle is
![]() $\overline{c}.$
Consider the tensor product representation
$\overline{c}.$
Consider the tensor product representation
![]() $\widetilde{\sigma}\otimes \tau$
of
$\widetilde{\sigma}\otimes \tau$
of
![]() $G_\sigma.$
Lemma 5 shows that
$G_\sigma.$
Lemma 5 shows that
![]() $\widetilde{\sigma}\otimes \tau$
is a projective representation for the cocyle
$\widetilde{\sigma}\otimes \tau$
is a projective representation for the cocyle
![]() $c\overline{c}=1.$
So,
$c\overline{c}=1.$
So,
![]() $\widetilde{\sigma}\otimes \tau$
is a measurable homomorphism from
$\widetilde{\sigma}\otimes \tau$
is a measurable homomorphism from
![]() $G_\sigma$
to
$G_\sigma$
to
![]() $U(m).$
This implies that
$U(m).$
This implies that
![]() $\widetilde{\sigma}\otimes \tau$
is continuous (see [
Reference Bekka, de la Harpe and ValetteBHV08
, lemma A·6·2]) and so
$\widetilde{\sigma}\otimes \tau$
is continuous (see [
Reference Bekka, de la Harpe and ValetteBHV08
, lemma A·6·2]) and so
![]() $\widetilde{\sigma}\otimes \tau$
is an ordinary representation of
$\widetilde{\sigma}\otimes \tau$
is an ordinary representation of
![]() $G_\sigma$
.
$G_\sigma$
.
It is clear that
![]() $\widetilde{\sigma}\otimes \tau$
is finite dimensional. Observe that the restriction
$\widetilde{\sigma}\otimes \tau$
is finite dimensional. Observe that the restriction
![]() $(\widetilde{\sigma}\otimes \tau)|_N$
of
$(\widetilde{\sigma}\otimes \tau)|_N$
of
![]() $\widetilde{\sigma}\otimes \tau$
to N is a multiple of
$\widetilde{\sigma}\otimes \tau$
to N is a multiple of
![]() $\sigma.$
Let
$\sigma.$
Let
Then
![]() $\rho$
is finite dimensional, since
$\rho$
is finite dimensional, since
![]() $\widetilde{\sigma}\otimes \tau$
is finite dimensional and
$\widetilde{\sigma}\otimes \tau$
is finite dimensional and
![]() $G_\sigma$
has finite index in G. As
$G_\sigma$
has finite index in G. As
![]() $G_\sigma$
is open in G,
$G_\sigma$
is open in G,
![]() $\widetilde{\sigma}\otimes \tau$
is equivalent to a subrepresentation of the restriction
$\widetilde{\sigma}\otimes \tau$
is equivalent to a subrepresentation of the restriction
![]() $\rho|_{G_\sigma}$
of
$\rho|_{G_\sigma}$
of
![]() $\rho$
to
$\rho$
to
![]() $G_\sigma$
(see e.g. [
Reference Bekka and de la HarpeBdlH
, 1·F]); consequently,
$G_\sigma$
(see e.g. [
Reference Bekka and de la HarpeBdlH
, 1·F]); consequently,
![]() $\sigma$
is equivalent to a subrepresentation of
$\sigma$
is equivalent to a subrepresentation of
![]() $\rho|_{N}$
. Since
$\rho|_{N}$
. Since
![]() $\rho$
is a finite dimensional unitary representation of G, there exists a unitary representation
$\rho$
is a finite dimensional unitary representation of G, there exists a unitary representation
![]() $\widehat{\rho}$
of
$\widehat{\rho}$
of
![]() ${\rm Bohr}(G)$
such that
${\rm Bohr}(G)$
such that
![]() $\widehat{\rho}\circ \beta_G= \rho.$
So,
$\widehat{\rho}\circ \beta_G= \rho.$
So,
![]() $\sigma$
is equivalent to a subrepresentation of
$\sigma$
is equivalent to a subrepresentation of
![]() $(\widehat{\rho}\circ \beta_G)|_N$
, that is, there exists a subspace V of the space of
$(\widehat{\rho}\circ \beta_G)|_N$
, that is, there exists a subspace V of the space of
![]() $\widehat{\rho}$
which is invariant under
$\widehat{\rho}$
which is invariant under
![]() $\beta_G(N)$
and defining a representation of N which is equivalent to
$\beta_G(N)$
and defining a representation of N which is equivalent to
![]() $\sigma.$
Then V is invariant under
$\sigma.$
Then V is invariant under
![]() $K=\overline{\beta_G(N)}$
and defines therefore an irreducible representation
$K=\overline{\beta_G(N)}$
and defines therefore an irreducible representation
![]() $\widehat{\sigma}$
of K for which
$\widehat{\sigma}$
of K for which
![]() $\widehat{\sigma}\circ (\beta_G|_N)= \sigma$
holds.
$\widehat{\sigma}\circ (\beta_G|_N)= \sigma$
holds.
Let
![]() $\varphi_N\,:\, {\rm Bohr}(N)\to K=\overline{\beta_G(N)}$
be the homomorphism such that
$\varphi_N\,:\, {\rm Bohr}(N)\to K=\overline{\beta_G(N)}$
be the homomorphism such that
![]() $\varphi_N\circ \beta_N= \beta_G|_N$
.
$\varphi_N\circ \beta_N= \beta_G|_N$
.
-
(iii) Third step. We claim that
where \begin{equation*}{{\rm Ker}} \varphi_N =\bigcap_{\sigma \in \widehat{N}_{ \rm fd}^{H-{\rm per}}} {{\rm Ker}} ({\rm Bohr}({\sigma})),\end{equation*}
\begin{equation*}{{\rm Ker}} \varphi_N =\bigcap_{\sigma \in \widehat{N}_{ \rm fd}^{H-{\rm per}}} {{\rm Ker}} ({\rm Bohr}({\sigma})),\end{equation*}
 ${\rm Bohr}({\sigma})$
is the representation of
${\rm Bohr}({\sigma})$
is the representation of
 ${\rm Bohr}(N)$
such that
${\rm Bohr}(N)$
such that
 ${\rm Bohr}({\sigma})\circ \beta_N= \sigma.$
${\rm Bohr}({\sigma})\circ \beta_N= \sigma.$
Indeed, by the first and second steps, we have
since obviously
![]() $\widehat{\sigma} \circ \varphi_N= {\rm Bohr}({\sigma})$
for
$\widehat{\sigma} \circ \varphi_N= {\rm Bohr}({\sigma})$
for
![]() $\sigma= (\widehat{\sigma} \circ \varphi_N) \circ \beta_N,$
it follows that
$\sigma= (\widehat{\sigma} \circ \varphi_N) \circ \beta_N,$
it follows that
As
![]() $\varphi_N({\rm Bohr}(N))=K$
and
$\varphi_N({\rm Bohr}(N))=K$
and
![]() $\widehat{K}$
separates the points of K, we have
$\widehat{K}$
separates the points of K, we have
![]() $\bigcap_{\widehat{\sigma} \in \widehat{K}} {{\rm Ker}} (\widehat{\sigma} \circ \varphi_N)={{\rm Ker}} \varphi_N$
and the claim is proved.
$\bigcap_{\widehat{\sigma} \in \widehat{K}} {{\rm Ker}} (\widehat{\sigma} \circ \varphi_N)={{\rm Ker}} \varphi_N$
and the claim is proved.
Set
![]() $L\,:\!=\, \overline{\beta_G(H)}.$
$L\,:\!=\, \overline{\beta_G(H)}.$
-
(iv) Fourth step. We claim that the map
 $\varphi_H\,:\, {\rm Bohr}(H)\to L,$
defined by the relation
$\varphi_H\,:\, {\rm Bohr}(H)\to L,$
defined by the relation
 $\varphi_H\circ \beta_H= \beta_G|_H,$
is an isomorphism. Indeed, the canonical isomorphism
$\varphi_H\circ \beta_H= \beta_G|_H,$
is an isomorphism. Indeed, the canonical isomorphism
 $H\to G/N$
induces an isomorphism
$H\to G/N$
induces an isomorphism
 ${\rm Bohr}(H) \to {\rm Bohr}(G/N)$
. Using Proposition 7 (i), we obtain a continuous epimorphism such that
${\rm Bohr}(H) \to {\rm Bohr}(G/N)$
. Using Proposition 7 (i), we obtain a continuous epimorphism such that \begin{equation*}f\,:\,L\to {\rm Bohr}(H)\end{equation*}
\begin{equation*}f\,:\,L\to {\rm Bohr}(H)\end{equation*}
 $f(\beta_G(h))= \beta_H(h)$
for all
$f(\beta_G(h))= \beta_H(h)$
for all
 $h\in H.$
Then
$h\in H.$
Then
 $\varphi_H\circ f$
is the identity on
$\varphi_H\circ f$
is the identity on
 $\beta_G(H)$
and hence on L, by density. This implies that
$\beta_G(H)$
and hence on L, by density. This implies that
 $\varphi_H$
is an isomorphism.
$\varphi_H$
is an isomorphism.
Observe that, by the universal property of
![]() ${\rm Bohr}(N),$
every element
${\rm Bohr}(N),$
every element
![]() $h\in H$
defines a continuous automorphism
$h\in H$
defines a continuous automorphism
![]() $\theta_b(h)$
of
$\theta_b(h)$
of
![]() ${\rm Bohr}(N) $
such that
${\rm Bohr}(N) $
such that
The corresponding homomorphism
![]() $\theta_b\,:\,H\to {{\rm Aut}}({\rm Bohr}(N))$
defines an action of H on the compact group
$\theta_b\,:\,H\to {{\rm Aut}}({\rm Bohr}(N))$
defines an action of H on the compact group
![]() ${\rm Bohr}(N).$
By duality, we have an action, still denoted by
${\rm Bohr}(N).$
By duality, we have an action, still denoted by
![]() $\theta_b,$
of H on
$\theta_b,$
of H on
![]() $\widehat{{\rm Bohr}(N)}$
and we have
$\widehat{{\rm Bohr}(N)}$
and we have
This implies that the normal subgroup
of
![]() ${\rm Bohr}(N)$
is H-invariant. We have therefore an induced action
${\rm Bohr}(N)$
is H-invariant. We have therefore an induced action
![]() $\overline{\theta_b}$
of H on
$\overline{\theta_b}$
of H on
![]() ${\rm Bohr}(N)/{{\rm Ker}}\varphi_N.$
Observe that the isomorphism
${\rm Bohr}(N)/{{\rm Ker}}\varphi_N.$
Observe that the isomorphism
induced by
![]() $\varphi_N$
is H-equivariant for
$\varphi_N$
is H-equivariant for
![]() $\overline{\theta_b}$
and the action of H on K given by conjugation with
$\overline{\theta_b}$
and the action of H on K given by conjugation with
![]() $\beta_G(h)$
for
$\beta_G(h)$
for
![]() $h\in H.$
$h\in H.$
-
(v) Fifth step. We claim that the action
 $\overline{\theta_b}$
induces an action of
$\overline{\theta_b}$
induces an action of
 ${\rm Bohr}(H)$
by automorphisms on
${\rm Bohr}(H)$
by automorphisms on
 ${\rm Bohr}(N)/{{\rm Ker}} \varphi_N$
and that the map is an isomorphism.
${\rm Bohr}(N)/{{\rm Ker}} \varphi_N$
and that the map is an isomorphism. \begin{equation*}({\rm Bohr}(N)/{{\rm Ker}}\varphi_N) \rtimes {\rm Bohr}(H)\to {\rm Bohr}(G), (x {{\rm Ker}}\varphi_N, y) \mapsto \varphi_N(x)\varphi_H(y)\end{equation*}
\begin{equation*}({\rm Bohr}(N)/{{\rm Ker}}\varphi_N) \rtimes {\rm Bohr}(H)\to {\rm Bohr}(G), (x {{\rm Ker}}\varphi_N, y) \mapsto \varphi_N(x)\varphi_H(y)\end{equation*}
Indeed,
![]() $\overline{\beta_G(N)}$
is a normal subgroup of
$\overline{\beta_G(N)}$
is a normal subgroup of
![]() ${\rm Bohr}(G)$
and so
${\rm Bohr}(G)$
and so
![]() $\overline{\beta_G(H)}$
acts by conjugation on K. By the third and the fourth step, the maps
$\overline{\beta_G(H)}$
acts by conjugation on K. By the third and the fourth step, the maps
and
are isomorphisms. We define an action
by
for
![]() $x\in {\rm Bohr}(N)$
and
$x\in {\rm Bohr}(N)$
and
![]() $y\in {\rm Bohr}(H).$
The claim follows.
$y\in {\rm Bohr}(H).$
The claim follows.
3·2. Proof of Theorem B
The proof is similar to the proof of Theorem A. The role of
![]() $\widehat{N}_{ \rm fd}$
is now played by the space
$\widehat{N}_{ \rm fd}$
is now played by the space
![]() $\widehat{N}_{ \rm finite}$
of finite dimensional irreducible representations of N with finite image. We will go quickly through the steps of the proof of Theorem A; at some places (especially the second step) there will be a few crucial changes and new arguments which we will emphasise.
$\widehat{N}_{ \rm finite}$
of finite dimensional irreducible representations of N with finite image. We will go quickly through the steps of the proof of Theorem A; at some places (especially the second step) there will be a few crucial changes and new arguments which we will emphasise.
Set
![]() $L\,:\!=\, \overline{\alpha_G(N)},$
where
$L\,:\!=\, \overline{\alpha_G(N)},$
where
![]() $\alpha_G\,:\,G \to {\rm Prof}(G)$
is the canonical map. Observe that L is profinite.
$\alpha_G\,:\,G \to {\rm Prof}(G)$
is the canonical map. Observe that L is profinite.
-
(i) First step. We claim that
 $ \left\{\widehat{\sigma}\circ (\alpha_G|_N)\,:\,\widehat{\sigma} \in \widehat{L}\right\} \subset \widehat{N}_{ \rm finite}^{H-{\rm per}}. $
Indeed, let
$ \left\{\widehat{\sigma}\circ (\alpha_G|_N)\,:\,\widehat{\sigma} \in \widehat{L}\right\} \subset \widehat{N}_{ \rm finite}^{H-{\rm per}}. $
Indeed, let
 $\widehat{\sigma} \in \widehat{L}$
. Then
$\widehat{\sigma} \in \widehat{L}$
. Then
 $\sigma\,:\!=\, \widehat{\sigma}\circ (\alpha_G|_N)\in \widehat{N}_{ \rm finite},$
since L is profinite. Let
$\sigma\,:\!=\, \widehat{\sigma}\circ (\alpha_G|_N)\in \widehat{N}_{ \rm finite},$
since L is profinite. Let
 $ \widehat{\rho}$
be an irreducible subrepresentation of
$ \widehat{\rho}$
be an irreducible subrepresentation of
 ${\rm Ind}_{L}^{{\rm Prof}(G)} \widehat{\sigma}.$
Since
${\rm Ind}_{L}^{{\rm Prof}(G)} \widehat{\sigma}.$
Since
 ${\rm Prof}(G)$
is compact,
${\rm Prof}(G)$
is compact,
 $\widehat{\rho}$
is finite dimensional. Since
$\widehat{\rho}$
is finite dimensional. Since
 $\sigma$
is equivalent to a subrepresentation of
$\sigma$
is equivalent to a subrepresentation of
 $\widehat{\rho} \circ (\alpha_G)|N)$
, it has therefore a finite H-orbit.
$\widehat{\rho} \circ (\alpha_G)|N)$
, it has therefore a finite H-orbit. -
(ii) Second step. We claim that
 $ \widehat{N}_{ \rm finite}^{H-{\rm per}} \subset \left\{\widehat{\sigma} \circ (\alpha_G|_N)\,:\,\widehat{\sigma} \in \widehat{L}\right\}. $
Indeed, let
$ \widehat{N}_{ \rm finite}^{H-{\rm per}} \subset \left\{\widehat{\sigma} \circ (\alpha_G|_N)\,:\,\widehat{\sigma} \in \widehat{L}\right\}. $
Indeed, let
 $\sigma\,:\,N\to U(m)$
be an irreducible representation with finite image. By Proposition 6, there exists a projective representation
$\sigma\,:\,N\to U(m)$
be an irreducible representation with finite image. By Proposition 6, there exists a projective representation
 $\widetilde{\sigma}$
of
$\widetilde{\sigma}$
of
 $G_\sigma=NH_\sigma$
which extends
$G_\sigma=NH_\sigma$
which extends
 $\sigma$
and the associated cocycle
$\sigma$
and the associated cocycle
 $c\,:\,G_\sigma\times G_\sigma\to \textbf{S}^1$
, factorises through
$c\,:\,G_\sigma\times G_\sigma\to \textbf{S}^1$
, factorises through
 $H_\sigma\times H_\sigma$
. We need to show that we can choose
$H_\sigma\times H_\sigma$
. We need to show that we can choose
 $\widetilde{\sigma}$
so that
$\widetilde{\sigma}$
so that
 $\widetilde{\sigma}(G_\sigma)$
is finite.
$\widetilde{\sigma}(G_\sigma)$
is finite.
Choose a projective representation
![]() $\widetilde{\sigma}\,:\,G_\sigma \to U(m)$
as above and modify
$\widetilde{\sigma}\,:\,G_\sigma \to U(m)$
as above and modify
![]() $\widetilde{\sigma}$
as follows: define
$\widetilde{\sigma}$
as follows: define
Then
![]() $\widetilde{\sigma}_1$
is again a projective representation of
$\widetilde{\sigma}_1$
is again a projective representation of
![]() $G_\sigma=NH_\sigma$
which extends
$G_\sigma=NH_\sigma$
which extends
![]() $\sigma$
and the associated cocycle
$\sigma$
and the associated cocycle
![]() $c\,:\,G_\sigma\times G_\sigma\to \textbf{S}^1$
factorises through
$c\,:\,G_\sigma\times G_\sigma\to \textbf{S}^1$
factorises through
![]() $H_\sigma\times H_\sigma$
; moreover,
$H_\sigma\times H_\sigma$
; moreover,
![]() $\widetilde{\sigma}_1(h)\in SU(m)$
for every
$\widetilde{\sigma}_1(h)\in SU(m)$
for every
![]() $h\in H_\sigma.$
$h\in H_\sigma.$
Every
![]() $h\in H_\sigma$
induces a bijection
$h\in H_\sigma$
induces a bijection
![]() $\varphi_h$
of
$\varphi_h$
of
![]() $\sigma(N)$
given by
$\sigma(N)$
given by
So, we have a map
where
![]() ${\rm Sym}(\sigma(N))$
is the set of bijections of
${\rm Sym}(\sigma(N))$
is the set of bijections of
![]() $\sigma(N).$
For
$\sigma(N).$
For
![]() $h_1, h_2\in H_\sigma,$
we have
$h_1, h_2\in H_\sigma,$
we have
![]() $\varphi_{h_1}= \varphi_{h_2}$
if and only if
$\varphi_{h_1}= \varphi_{h_2}$
if and only if
![]() $\widetilde{\sigma}_1(h_2)= \lambda \widetilde{\sigma}_1(h_1)$
for some scalar
$\widetilde{\sigma}_1(h_2)= \lambda \widetilde{\sigma}_1(h_1)$
for some scalar
![]() $ \lambda \in \textbf{S}^1,$
by irreducibility of
$ \lambda \in \textbf{S}^1,$
by irreducibility of
![]() $\sigma$
. Since
$\sigma$
. Since
![]() $\det(\widetilde{\sigma}_1(h_1))=1$
and
$\det(\widetilde{\sigma}_1(h_1))=1$
and
![]() $\det (\widetilde{\sigma}_1(h_2))=1,$
it follows that
$\det (\widetilde{\sigma}_1(h_2))=1,$
it follows that
![]() $\lambda$
is a mth root of unity. This shows that the fibers of the map
$\lambda$
is a mth root of unity. This shows that the fibers of the map
![]() $\varphi$
are finite. Since
$\varphi$
are finite. Since
![]() $\sigma(N)$
is finite,
$\sigma(N)$
is finite,
![]() ${\rm Sym}(\sigma(N))$
and hence
${\rm Sym}(\sigma(N))$
and hence
![]() $\widetilde{\sigma}_1(H_\sigma)$
is finite. It follows that
$\widetilde{\sigma}_1(H_\sigma)$
is finite. It follows that
![]() $\widetilde{\sigma}_1(G_\sigma)= \widetilde{\sigma}_1(H_\sigma)\sigma(N)$
is finite.
$\widetilde{\sigma}_1(G_\sigma)= \widetilde{\sigma}_1(H_\sigma)\sigma(N)$
is finite.
Let
![]() $\tau\,:\,G_\sigma\to U(m)$
be the projective representation of
$\tau\,:\,G_\sigma\to U(m)$
be the projective representation of
![]() $G_\sigma$
given by
$G_\sigma$
given by
Then
![]() $\widetilde{\sigma}_1\otimes \tau$
is a ordinary representation of
$\widetilde{\sigma}_1\otimes \tau$
is a ordinary representation of
![]() $G_\sigma$
and has finite image. The induced representation
$G_\sigma$
and has finite image. The induced representation
![]() $\rho\,:\!=\,{\rm Ind}_{G_\sigma}^G (\widetilde{\sigma}_1\otimes \tau)$
has finite image, since
$\rho\,:\!=\,{\rm Ind}_{G_\sigma}^G (\widetilde{\sigma}_1\otimes \tau)$
has finite image, since
![]() $G_\sigma$
has finite index in G. As
$G_\sigma$
has finite index in G. As
![]() $\widetilde{\sigma}_1\otimes \tau$
is equivalent to a subrepresentation of the restriction
$\widetilde{\sigma}_1\otimes \tau$
is equivalent to a subrepresentation of the restriction
![]() $\rho|_{G_\sigma}$
of
$\rho|_{G_\sigma}$
of
![]() $\rho$
to
$\rho$
to
![]() $G_\sigma,$
the representation
$G_\sigma,$
the representation
![]() $\sigma$
is equivalent to a subrepresentation of
$\sigma$
is equivalent to a subrepresentation of
![]() $\rho|_{N}$
. Since
$\rho|_{N}$
. Since
![]() $\rho(G)$
has finite image, there exists a unitary representation
$\rho(G)$
has finite image, there exists a unitary representation
![]() $\widehat{\rho}$
of
$\widehat{\rho}$
of
![]() ${\rm Prof}(G)$
such that
${\rm Prof}(G)$
such that
![]() $\widehat{\rho}\circ \alpha_G= \rho.$
So, there exists a subspace V of the space of
$\widehat{\rho}\circ \alpha_G= \rho.$
So, there exists a subspace V of the space of
![]() $\widehat{\rho}$
which is invariant under
$\widehat{\rho}$
which is invariant under
![]() $\alpha_G(N)$
and defining a representation of N which is equivalent to
$\alpha_G(N)$
and defining a representation of N which is equivalent to
![]() $\sigma.$
Then V defines an irreducible representation
$\sigma.$
Then V defines an irreducible representation
![]() $\widehat{\sigma}$
of L for which
$\widehat{\sigma}$
of L for which
![]() $\widehat{\sigma}\circ (\alpha_G|_N)= \sigma$
holds.
$\widehat{\sigma}\circ (\alpha_G|_N)= \sigma$
holds.
Let
![]() $\psi_N\,:\,{\rm Prof}(N)\to L$
be the homomorphism such that
$\psi_N\,:\,{\rm Prof}(N)\to L$
be the homomorphism such that
![]() $\psi_N\circ \alpha_N= \alpha_G|_N$
.
$\psi_N\circ \alpha_N= \alpha_G|_N$
.
-
(iii) Third step. We claim that
Indeed, the proof is similar to the proof of the third step of Theorem A \begin{equation*}{{\rm Ker}} \psi_N =\bigcap_{\sigma \in \widehat{N}_{ \rm finite}^{H-{\rm per}}} {{\rm Ker}} ({\rm Prof}(\sigma)).\end{equation*}
\begin{equation*}{{\rm Ker}} \psi_N =\bigcap_{\sigma \in \widehat{N}_{ \rm finite}^{H-{\rm per}}} {{\rm Ker}} ({\rm Prof}(\sigma)).\end{equation*}
-
(iv) Fourth step. We claim that the map
 $\psi_H\,:\,{\rm Prof}(H)\to \overline{\alpha_G(H)},$
defined by the relation
$\psi_H\,:\,{\rm Prof}(H)\to \overline{\alpha_G(H)},$
defined by the relation
 $\varphi_H\circ \alpha_H= \alpha_G|_H,$
is an isomorphism. Indeed, the proof is similar to the proof of the fourth step of Theorem A.
$\varphi_H\circ \alpha_H= \alpha_G|_H,$
is an isomorphism. Indeed, the proof is similar to the proof of the fourth step of Theorem A.
Every element
![]() $h\in H$
defines a continuous automorphism
$h\in H$
defines a continuous automorphism
![]() $\theta_p(h)$
of
$\theta_p(h)$
of
![]() ${\rm Prof}(N).$
Let
${\rm Prof}(N).$
Let
be the corresponding homomorphism; as in Theorem A, we have an induced action
![]() $\overline{\theta_p}$
of H on
$\overline{\theta_p}$
of H on
![]() ${\rm Prof}(N)/{{\rm Ker}}\psi_N.$
${\rm Prof}(N)/{{\rm Ker}}\psi_N.$
-
• Fifth step. We claim that the action
 $\overline{\theta_p}$
of H induces an action of
$\overline{\theta_p}$
of H induces an action of
 ${\rm Prof}(H)$
by automorphisms on
${\rm Prof}(H)$
by automorphisms on
 ${\rm Prof}(N)/{{\rm Ker}} \psi_N$
and that the map is an isomorphism.
${\rm Prof}(N)/{{\rm Ker}} \psi_N$
and that the map is an isomorphism. \begin{equation*}\left({\rm Prof}(N)/{{\rm Ker}}\psi_N\right) \rtimes {\rm Prof}(H)\to {\rm Prof}(G), (x {{\rm Ker}}\psi_N, y) \mapsto \psi_N(x)\psi_H(y)\end{equation*}
\begin{equation*}\left({\rm Prof}(N)/{{\rm Ker}}\psi_N\right) \rtimes {\rm Prof}(H)\to {\rm Prof}(G), (x {{\rm Ker}}\psi_N, y) \mapsto \psi_N(x)\psi_H(y)\end{equation*}
Indeed, the proof is similar to the proof of the fifth step of Theorem A.
4. Proof of the Corollaries
4·1. Proof of Corollary C
Assume that N is finitely generated. In view of Theorem B, we have to show that
![]() $\widehat{N}_{ \rm finite}^{H-{\rm per}}= \widehat{N}_{ \rm finite}.$
$\widehat{N}_{ \rm finite}^{H-{\rm per}}= \widehat{N}_{ \rm finite}.$
It is well known that, for every integer
![]() $n\geq1,$
there are only finitely many subgroups of index n in N. Indeed, since N is finitely generated, there are only finitely many actions of N on the set
$n\geq1,$
there are only finitely many subgroups of index n in N. Indeed, since N is finitely generated, there are only finitely many actions of N on the set
![]() $\{1, \dots, n\}.$
Every subgroup M of index n defines an action of N on
$\{1, \dots, n\}.$
Every subgroup M of index n defines an action of N on
![]() $N/M$
and hence on
$N/M$
and hence on
![]() $\{1, \dots, n\}$
for which the stabiliser of, say, 1 is M. So, there are only finitely many such subgroups M.
$\{1, \dots, n\}$
for which the stabiliser of, say, 1 is M. So, there are only finitely many such subgroups M.
Let
![]() $\sigma \in \widehat{N}_{ \rm finite}$
and set
$\sigma \in \widehat{N}_{ \rm finite}$
and set
![]() $n\,:\!=\, |\sigma(N)|.$
Consider
$n\,:\!=\, |\sigma(N)|.$
Consider
![]() $N_\sigma= \cap_{ M} M,$
where M runs over the subgroups of N of index n. Then
$N_\sigma= \cap_{ M} M,$
where M runs over the subgroups of N of index n. Then
![]() $N_\sigma$
is a normal subgroup of N of finite index and, for every
$N_\sigma$
is a normal subgroup of N of finite index and, for every
![]() $h\in H,$
the representation
$h\in H,$
the representation
![]() $\sigma^h$
factorises to a representation of
$\sigma^h$
factorises to a representation of
![]() $N/N_\sigma.$
Since
$N/N_\sigma.$
Since
![]() $N/N_\sigma$
is a finite group, it has only finitely many non equivalent irreducible representations and the claim is proved.
$N/N_\sigma$
is a finite group, it has only finitely many non equivalent irreducible representations and the claim is proved.
4·2. Proof of Corollary D
We assume that N is abelian. The dual group of
![]() ${\rm Bohr}(N)$
is
${\rm Bohr}(N)$
is
![]() $\widehat{N}$
and the dual of
$\widehat{N}$
and the dual of
![]() ${\rm Prof}(N)$
is
${\rm Prof}(N)$
is
![]() $\widehat{N}_{\rm finite}$
, viewed as discrete groups. With the notation as in Theorems A and B, the subgroups C and D are respectively the annihilators in
$\widehat{N}_{\rm finite}$
, viewed as discrete groups. With the notation as in Theorems A and B, the subgroups C and D are respectively the annihilators in
![]() ${\rm Bohr}(N)$
and in
${\rm Bohr}(N)$
and in
![]() ${\rm Prof}(N)$
of the closed subgroups
${\rm Prof}(N)$
of the closed subgroups
![]() $\widehat{N}^{H-{\rm per}}$
and
$\widehat{N}^{H-{\rm per}}$
and
![]() $\widehat{N}_{ \rm finite}^{H-{\rm per}}$
. Hence,
$\widehat{N}_{ \rm finite}^{H-{\rm per}}$
. Hence,
![]() ${\rm Bohr}(N)/C$
and
${\rm Bohr}(N)/C$
and
![]() ${\rm Prof}(N)/D$
are the dual groups of
${\rm Prof}(N)/D$
are the dual groups of
![]() $\widehat{N}^{H-{\rm per}}$
and
$\widehat{N}^{H-{\rm per}}$
and
![]() $\widehat{N}_{ \rm finite}^{H-{\rm per}}$
, viewed as discrete groups. So, the claim follows from Theorems A and B.
$\widehat{N}_{ \rm finite}^{H-{\rm per}}$
, viewed as discrete groups. So, the claim follows from Theorems A and B.
4·3 Proof of Corollary E
In view of Theorems A and B, G is MAP, respectively RF, if and only if
respectively
So, G is MAP, respectively RF, if and only if
respectively
This exactly means that G is MAP, respectively RF, if and only if
![]() $\widehat{N}_{ \rm fd}^{H-{\rm per}}$
separates the points of N and H is MAP, respectively
$\widehat{N}_{ \rm fd}^{H-{\rm per}}$
separates the points of N and H is MAP, respectively
![]() $\widehat{N}_{ \rm finite}^{H-{\rm per}}$
separates the points of N and H is RF.
$\widehat{N}_{ \rm finite}^{H-{\rm per}}$
separates the points of N and H is RF.
4·4. Proof of Corollary F
We assume that
![]() $G= \Lambda\wr_X H$
is the wreath product of the groups
$G= \Lambda\wr_X H$
is the wreath product of the groups
![]() $\Lambda$
and H given by a transitive action
$\Lambda$
and H given by a transitive action
![]() $H\curvearrowright X;$
set
$H\curvearrowright X;$
set
![]() $N\,:\!=\,\oplus_{x\in X}\Lambda.$
$N\,:\!=\,\oplus_{x\in X}\Lambda.$
-
(a) Assume that X is finite. Then, of course,
 $\widehat{N}_{\rm fd}^{H-{\rm per}}=\widehat{N}_{\rm fd}$
and
$\widehat{N}_{\rm fd}^{H-{\rm per}}=\widehat{N}_{\rm fd}$
and
 $\widehat{N}_{ \rm finite}^{H-{\rm per}}=\widehat{N}_{\rm finite};$
so, the subgroups C and D from Theorems A and B are trivial. Since
$\widehat{N}_{ \rm finite}^{H-{\rm per}}=\widehat{N}_{\rm finite};$
so, the subgroups C and D from Theorems A and B are trivial. Since
 ${\rm Bohr}(N)=\oplus_{x\in X}{\rm Bohr}(\Lambda)$
and
${\rm Bohr}(N)=\oplus_{x\in X}{\rm Bohr}(\Lambda)$
and
 $ {\rm Prof}(N)= \oplus_{x\in X}{\rm Prof}(\Lambda),$
we have
$ {\rm Prof}(N)= \oplus_{x\in X}{\rm Prof}(\Lambda),$
we have  \[\begin{aligned}&{\rm Bohr}(\Lambda\wr_X H)\cong \left( \oplus_{x\in X}{\rm Bohr}(\Lambda)\right) \rtimes {\rm Bohr}(H) \ \text{and}\\&{\rm Prof}(\Lambda\wr_X H)\cong \left( \oplus_{x\in X}{\rm Prof}(\Lambda)\right) \rtimes {\rm Prof}(H).\end{aligned}\]
\[\begin{aligned}&{\rm Bohr}(\Lambda\wr_X H)\cong \left( \oplus_{x\in X}{\rm Bohr}(\Lambda)\right) \rtimes {\rm Bohr}(H) \ \text{and}\\&{\rm Prof}(\Lambda\wr_X H)\cong \left( \oplus_{x\in X}{\rm Prof}(\Lambda)\right) \rtimes {\rm Prof}(H).\end{aligned}\]
-
(b) Assume that X is infinite.
-
(i) First step. We claim that, for every
 $\sigma \in \widehat{N}_{\rm fd}^{H-{\rm per}},$
we have
$\sigma \in \widehat{N}_{\rm fd}^{H-{\rm per}},$
we have
 $\dim \sigma =1$
, that is,
$\dim \sigma =1$
, that is,
 $\sigma (N)\subset U(1)=\textbf{S}^1.$
$\sigma (N)\subset U(1)=\textbf{S}^1.$
Indeed, assume by contradiction that
![]() $\dim \sigma >1$
. Let
$\dim \sigma >1$
. Let
![]() $\mathcal{F}$
be the family of finite subsets of X. For every
$\mathcal{F}$
be the family of finite subsets of X. For every
![]() $F\in \mathcal{F},$
let N(F) be the normal subgroup of N given by
$F\in \mathcal{F},$
let N(F) be the normal subgroup of N given by
The restriction
![]() $\sigma|_{N(F)}$
of
$\sigma|_{N(F)}$
of
![]() $\sigma$
to N(F) has a decomposition into isotypical components:
$\sigma$
to N(F) has a decomposition into isotypical components:
where
![]() $\Sigma_F$
is a (finite) subset of
$\Sigma_F$
is a (finite) subset of
![]() $ \widehat{N(F)}_{\rm fd}$
and the
$ \widehat{N(F)}_{\rm fd}$
and the
![]() $n_\pi$
’s some positive integers. As is well known (see, e.g., [
Reference WeilWei40
, section 17]), every representation in
$n_\pi$
’s some positive integers. As is well known (see, e.g., [
Reference WeilWei40
, section 17]), every representation in
![]() $\widehat{N(F)}_{\rm fd}$
is a tensor product
$\widehat{N(F)}_{\rm fd}$
is a tensor product
![]() $\otimes_{h\in F}\rho_h$
of irreducible representations
$\otimes_{h\in F}\rho_h$
of irreducible representations
![]() $\rho_h$
of
$\rho_h$
of
![]() $\Lambda$
; so, we can view
$\Lambda$
; so, we can view
![]() $\Sigma_F$
as subset of
$\Sigma_F$
as subset of
![]() $\prod_{x\in F}\widehat{\Lambda}_{\rm fd}.$
If
$\prod_{x\in F}\widehat{\Lambda}_{\rm fd}.$
If
![]() $F\subset F',$
then the obvious map
$F\subset F',$
then the obvious map
![]() $\prod_{x\in F'}\widehat{\Lambda}_{\rm fd}\to \prod_{x\in F}\widehat{\Lambda}_{\rm fd}$
restricts to a surjective map
$\prod_{x\in F'}\widehat{\Lambda}_{\rm fd}\to \prod_{x\in F}\widehat{\Lambda}_{\rm fd}$
restricts to a surjective map
![]() $\Sigma_{F^{\prime}} \to \Sigma_F$
.
$\Sigma_{F^{\prime}} \to \Sigma_F$
.
Since
![]() $\dim \sigma$
is finite, it follows that there exists
$\dim \sigma$
is finite, it follows that there exists
![]() $F_0\in \mathcal{F}$
such that
$F_0\in \mathcal{F}$
such that
and
For
![]() $h\in H$
and
$h\in H$
and
![]() $F\in \mathcal{F},$
observe that for the decomposition of
$F\in \mathcal{F},$
observe that for the decomposition of
![]() $\sigma^h|_{N( h^{-1}F)}$
into isotypical components, we have
$\sigma^h|_{N( h^{-1}F)}$
into isotypical components, we have
So,
![]() $\sigma^{h}$
and
$\sigma^{h}$
and
![]() $\sigma$
are not equivalent if
$\sigma$
are not equivalent if
![]() $h^{-1}F_0\cap F_0=\emptyset.$
$h^{-1}F_0\cap F_0=\emptyset.$
Since X is infinite, we can choose inductively a sequence
![]() $(h_n)_{n\geq 0}$
of elements in H by
$(h_n)_{n\geq 0}$
of elements in H by
![]() $h_0=e$
and
$h_0=e$
and
The
![]() $\sigma^{h_n}$
’s are then pairwise not equivalent. This is a contradiction, since
$\sigma^{h_n}$
’s are then pairwise not equivalent. This is a contradiction, since
![]() $\sigma \in \widehat{N}_{\rm fd}^{H-{\rm per}}.$
$\sigma \in \widehat{N}_{\rm fd}^{H-{\rm per}}.$
Let
![]() $p:\Lambda\wr_X H\to \Lambda^{\rm Ab}\wr_X H$
be the quotient map, which is given by
$p:\Lambda\wr_X H\to \Lambda^{\rm Ab}\wr_X H$
be the quotient map, which is given by
-
(ii) Second step. We claim that the induced maps
and \begin{equation*}{\rm Bohr}(p)\,:\, {\rm Bohr}(\Lambda\wr_X H)\to {\rm Bohr}( \Lambda^{\rm Ab}\wr_X H)\end{equation*}
are isomorphisms.
\begin{equation*}{\rm Bohr}(p)\,:\, {\rm Bohr}(\Lambda\wr_X H)\to {\rm Bohr}( \Lambda^{\rm Ab}\wr_X H)\end{equation*}
are isomorphisms. \begin{equation*} {\rm Prof}(p)\,:\,{\rm Prof}(\Lambda\wr_X H)\to {\rm Prof}( \Lambda^{\rm Ab}\wr_X H) \end{equation*}
\begin{equation*} {\rm Prof}(p)\,:\,{\rm Prof}(\Lambda\wr_X H)\to {\rm Prof}( \Lambda^{\rm Ab}\wr_X H) \end{equation*}
Indeed, by the first step, every
![]() $\sigma \in \widehat{N}_{\rm fd}^{H-{\rm per}}$
factorises through
$\sigma \in \widehat{N}_{\rm fd}^{H-{\rm per}}$
factorises through
![]() $ N^{\rm Ab}.$
Hence, by Theorems A and B, [N, N] is contained in
$ N^{\rm Ab}.$
Hence, by Theorems A and B, [N, N] is contained in
![]() $C=\ker \varphi_N$
and [N, N] is contained in
$C=\ker \varphi_N$
and [N, N] is contained in
![]() $D=\ker \psi_N$
. This means that
$D=\ker \psi_N$
. This means that
![]() $\beta_G(\ker p)= \{e\}$
and
$\beta_G(\ker p)= \{e\}$
and
![]() $\alpha_G(\ker p)= \{e\}$
. The claim follows then from Proposition 7.
$\alpha_G(\ker p)= \{e\}$
. The claim follows then from Proposition 7.
4·5. Proof of Corollary G
We assume that
![]() $G= \Lambda\wr_X H$
is the wreath product of the groups
$G= \Lambda\wr_X H$
is the wreath product of the groups
![]() $\Lambda$
and H given by an action
$\Lambda$
and H given by an action
![]() $H\curvearrowright X.$
We assume that
$H\curvearrowright X.$
We assume that
![]() $\Lambda$
has at least two elements and, as before, we set
$\Lambda$
has at least two elements and, as before, we set
![]() $N=\oplus_{x\in X}\Lambda .$
$N=\oplus_{x\in X}\Lambda .$
-
(a) Assume that X is finite. Then G is MAP (respectively RF) if and only if
 $\Lambda$
and H are MAP (respectively RF).
$\Lambda$
and H are MAP (respectively RF).
Indeed,
![]() $\widehat{N}_{ \rm fd}^{H-{\rm per}}= \widehat{N}_{ \rm fd}$
separates the points of N if and only if
$\widehat{N}_{ \rm fd}^{H-{\rm per}}= \widehat{N}_{ \rm fd}$
separates the points of N if and only if
![]() $\Lambda$
is MAP and
$\Lambda$
is MAP and
![]() $\widehat{N}_{ \rm finite}^{H-{\rm per}}=\widehat{N}_{ \rm finite}$
separates the points of N if and only if
$\widehat{N}_{ \rm finite}^{H-{\rm per}}=\widehat{N}_{ \rm finite}$
separates the points of N if and only if
![]() $\Lambda$
is RF. The claim follows then from Corollary E.
$\Lambda$
is RF. The claim follows then from Corollary E.
-
(b) Assume that X is infinite.
Assume that G is MAP. Then, for every H-orbit Y in X, the wreath product
![]() $\Lambda\wr_{Y} H,$
which embeds as subgroup of G, is MAP. Since some Y is infinite, Corollary F implies that
$\Lambda\wr_{Y} H,$
which embeds as subgroup of G, is MAP. Since some Y is infinite, Corollary F implies that
![]() $\Lambda$
is abelian. So, we may and will from now assume that
$\Lambda$
is abelian. So, we may and will from now assume that
![]() $\Lambda$
(and hence N) is abelian.
$\Lambda$
(and hence N) is abelian.
-
(i) First step. We claim that, if
 $\widehat{N}^{H-{\rm per}}$
separates the points of N, then
$\widehat{N}^{H-{\rm per}}$
separates the points of N, then
 $H\curvearrowright X$
is RF.
$H\curvearrowright X$
is RF.
Indeed, recall that the dual group
![]() $\widehat{\Lambda}$
of
$\widehat{\Lambda}$
of
![]() $\Lambda,$
equipped with the topology of pointwise convergence, is a compact group. The dual group
$\Lambda,$
equipped with the topology of pointwise convergence, is a compact group. The dual group
![]() $\widehat{N}$
of N can be identified, as topological group, with the product group
$\widehat{N}$
of N can be identified, as topological group, with the product group
![]() $\prod_{x\in X}\widehat{\Lambda},$
endowed with the product topology, by means of the duality
$\prod_{x\in X}\widehat{\Lambda},$
endowed with the product topology, by means of the duality
 \begin{equation*}\left \langle \prod_{x\in X}\chi_x, \oplus_{x\in X}\lambda_x\right\rangle= \prod_{x\in X}\chi_x(\lambda_x)\quad \text{for all} \quad \prod_{x\in X}\chi_x\in \widehat{N}, \oplus_{x\in X}\lambda_x\in N.\end{equation*}
\begin{equation*}\left \langle \prod_{x\in X}\chi_x, \oplus_{x\in X}\lambda_x\right\rangle= \prod_{x\in X}\chi_x(\lambda_x)\quad \text{for all} \quad \prod_{x\in X}\chi_x\in \widehat{N}, \oplus_{x\in X}\lambda_x\in N.\end{equation*}
(Observe that the product on the right hand side is well-defined since
![]() $\lambda_x=e$
for all but finitely many
$\lambda_x=e$
for all but finitely many
![]() $x\in X.$
) The dual action of H on
$x\in X.$
) The dual action of H on
![]() $\widehat{N}$
is given by
$\widehat{N}$
is given by
 \begin{equation*} \left(\prod_{x\in X}\chi_x\right)^h = \prod_{x\in X}\chi_{h^{-1}x} \qquad\text{for all}\quad h\in H. \end{equation*}
\begin{equation*} \left(\prod_{x\in X}\chi_x\right)^h = \prod_{x\in X}\chi_{h^{-1}x} \qquad\text{for all}\quad h\in H. \end{equation*}
For
![]() $\Phi\,:\!=\,\prod_{x\in X}\chi_x \in \widehat{N}$
, we have that
$\Phi\,:\!=\,\prod_{x\in X}\chi_x \in \widehat{N}$
, we have that
![]() $\Phi\in \widehat{N}^{H-{\rm per}}$
if and only if there exists a finite index subgroup
$\Phi\in \widehat{N}^{H-{\rm per}}$
if and only if there exists a finite index subgroup
![]() $H_\Phi$
of H such that
$H_\Phi$
of H such that
Let
![]() $x_0, x_1$
be two distinct points from X. By assumption,
$x_0, x_1$
be two distinct points from X. By assumption,
![]() $\widehat{N}^{H-{\rm per}}$
separates the points of N; equivalently,
$\widehat{N}^{H-{\rm per}}$
separates the points of N; equivalently,
![]() $\widehat{N}^{H-{\rm per}}$
is dense in
$\widehat{N}^{H-{\rm per}}$
is dense in
![]() $\widehat{N}$
. Since
$\widehat{N}$
. Since
![]() $\Lambda$
has at least two elements, we can find
$\Lambda$
has at least two elements, we can find
![]() $\chi^0\in \widehat{\Lambda}$
and
$\chi^0\in \widehat{\Lambda}$
and
![]() $\lambda_0\in \Lambda$
with
$\lambda_0\in \Lambda$
with
![]() $\chi^0(\lambda_0)\neq 1.$
Define
$\chi^0(\lambda_0)\neq 1.$
Define
![]() $\Phi_0= \prod_{x\in X}\chi_x\in \widehat{N}$
by
$\Phi_0= \prod_{x\in X}\chi_x\in \widehat{N}$
by
![]() $\chi_{x_0}= \chi^0$
and
$\chi_{x_0}= \chi^0$
and
![]() $\chi_x= 1_{\Lambda}$
for
$\chi_x= 1_{\Lambda}$
for
![]() $x\neq x_0.$
Set
$x\neq x_0.$
Set
Since
![]() $\widehat{N}^{H-{\rm per}}$
is dense in
$\widehat{N}^{H-{\rm per}}$
is dense in
![]() $\widehat{N}$
, we can find
$\widehat{N}$
, we can find
![]() $\Phi'= \prod_{x\in X}\chi_x^{\prime}\in \widehat{N}^{H-{\rm per}}$
such that
$\Phi'= \prod_{x\in X}\chi_x^{\prime}\in \widehat{N}^{H-{\rm per}}$
such that
We claim that
![]() $H_{\Phi^{\prime}} x_0\neq H_{\Phi^{\prime}} x_1$
, where
$H_{\Phi^{\prime}} x_0\neq H_{\Phi^{\prime}} x_1$
, where
![]() $H_{\Phi^{\prime}}$
is the stabiliser of
$H_{\Phi^{\prime}}$
is the stabiliser of
![]() $\Phi^{\prime}.$
Indeed, assume by contradiction that
$\Phi^{\prime}.$
Indeed, assume by contradiction that
![]() $ x_0\in H_{\Phi^{\prime}} x_1.$
Then
$ x_0\in H_{\Phi^{\prime}} x_1.$
Then
![]() $\chi_{x_0}^{\prime}= \chi_{x_1}^{\prime}$
and hence
$\chi_{x_0}^{\prime}= \chi_{x_1}^{\prime}$
and hence
 \[\begin{aligned}2\varepsilon&= |\chi^0(\lambda_0)-1|\\&\leq |\chi^0(\lambda_0)-\chi_{x_0}^{\prime}(\lambda_0)|+ |\chi_{x_0}^{\prime}(\lambda_0)- 1|\\ &=|\chi_{x_0}(\lambda_0)-\chi_{x_0}^{\prime}(\lambda_0)|+ | \chi_{x_1}^{\prime}(\lambda_0)- \chi_{x_1}(\lambda_0)| \\ &\leq \varepsilon \end{aligned}\]
\[\begin{aligned}2\varepsilon&= |\chi^0(\lambda_0)-1|\\&\leq |\chi^0(\lambda_0)-\chi_{x_0}^{\prime}(\lambda_0)|+ |\chi_{x_0}^{\prime}(\lambda_0)- 1|\\ &=|\chi_{x_0}(\lambda_0)-\chi_{x_0}^{\prime}(\lambda_0)|+ | \chi_{x_1}^{\prime}(\lambda_0)- \chi_{x_1}(\lambda_0)| \\ &\leq \varepsilon \end{aligned}\]
and this is a contradiction. Since
![]() $H_{\Phi^{\prime}}$
has finite index, we have proved that
$H_{\Phi^{\prime}}$
has finite index, we have proved that
![]() $H\curvearrowright X$
is RF.
$H\curvearrowright X$
is RF.
-
(ii) Second step. We claim that, if
 $H\curvearrowright X$
is RF, then
$H\curvearrowright X$
is RF, then
 $\widehat{N}^{H-{\rm per}}$
separates the points of N.
$\widehat{N}^{H-{\rm per}}$
separates the points of N.
Indeed, let
![]() $\oplus_{x\in X}\lambda_x\in N\setminus\{e\}.$
Then
$\oplus_{x\in X}\lambda_x\in N\setminus\{e\}.$
Then
![]() $F=\{x\in X \,:\,\lambda_x\neq e\}$
is a finite and non-empty subset of X. Let
$F=\{x\in X \,:\,\lambda_x\neq e\}$
is a finite and non-empty subset of X. Let
![]() $(\chi^0_x)_{x\in F}$
be a sequence in
$(\chi^0_x)_{x\in F}$
be a sequence in
![]() $ \widehat{\Lambda}$
such that
$ \widehat{\Lambda}$
such that
![]() $\prod_{x\in F} \chi^0_x(\lambda_x) \neq 1$
(this is possible, since abelian groups are MAP). Since
$\prod_{x\in F} \chi^0_x(\lambda_x) \neq 1$
(this is possible, since abelian groups are MAP). Since
![]() $H\curvearrowright X$
is RF, we can find a subgroup of finite index L of H so that
$H\curvearrowright X$
is RF, we can find a subgroup of finite index L of H so that
![]() $Lx \neq Lx^{\prime}$
for all
$Lx \neq Lx^{\prime}$
for all
![]() $x, x^{\prime}\in F$
with
$x, x^{\prime}\in F$
with
![]() $x\neq x^{\prime}.$
Define
$x\neq x^{\prime}.$
Define
![]() $\Phi= \prod_{x^{\prime}\in X}\chi_{x^{\prime}}\in \widehat{N}$
by
$\Phi= \prod_{x^{\prime}\in X}\chi_{x^{\prime}}\in \widehat{N}$
by
 \begin{equation*}\chi_{x^{\prime}}=\begin{cases}\chi^0_x& \text{if}\quad x^{\prime}\in Lx \quad \text{for some} \quad x\in F,\\1_{\Lambda}& \text{if}\quad x^{\prime}\notin \cup_{x\in F} Lh.\end{cases}\end{equation*}
\begin{equation*}\chi_{x^{\prime}}=\begin{cases}\chi^0_x& \text{if}\quad x^{\prime}\in Lx \quad \text{for some} \quad x\in F,\\1_{\Lambda}& \text{if}\quad x^{\prime}\notin \cup_{x\in F} Lh.\end{cases}\end{equation*}
It is clear that
![]() $L\subset H_{\Phi}$
and hence that
$L\subset H_{\Phi}$
and hence that
![]() $\Phi\in \widehat{N}^{H-{\rm per}}$
; moreover,
$\Phi\in \widehat{N}^{H-{\rm per}}$
; moreover,
So,
![]() $\widehat{N}^{H-{\rm per}}$
separates the points of N.
$\widehat{N}^{H-{\rm per}}$
separates the points of N.
-
(iii) Third step. We claim that, if
 $H\curvearrowright X$
is RF and
$H\curvearrowright X$
is RF and
 $\Lambda$
is RF, then
$\Lambda$
is RF, then
 $\widehat{N}_{\rm finite}^{H-{\rm per}}$
separates the points of N.
$\widehat{N}_{\rm finite}^{H-{\rm per}}$
separates the points of N.
The proof is the same as the proof of the second step, with only one difference: one has to choose a sequence
![]() $(\chi^0_x)_{x\in F}$
in
$(\chi^0_x)_{x\in F}$
in
![]() $ \widehat{\Lambda}_{\rm finite}$
such that
$ \widehat{\Lambda}_{\rm finite}$
such that
![]() $\prod_{x\in F} \chi^0_x(\lambda_x) \neq 1$
; this is possible, since we are assuming that
$\prod_{x\in F} \chi^0_x(\lambda_x) \neq 1$
; this is possible, since we are assuming that
![]() $\Lambda$
is RF.
$\Lambda$
is RF.
-
(iv) Fourth step. We claim that G is MAP if and only if H is RF and
 $H\curvearrowright X$
is RF. Indeed, this follows from Corollary E, combined with the first and second steps.
$H\curvearrowright X$
is RF. Indeed, this follows from Corollary E, combined with the first and second steps. -
(v) Fifth step. We claim that G is RF if and only if
 $\Lambda,H$
are RF and
$\Lambda,H$
are RF and
 $H\curvearrowright X$
is RF. Indeed, this follows from Corollary E, combined with the first and third steps.
$H\curvearrowright X$
is RF. Indeed, this follows from Corollary E, combined with the first and third steps.
5. Examples
5·1. Lamplighter group
For
![]() $m\geq 1,$
denote by
$m\geq 1,$
denote by
![]() $C_m$
the finite cyclic group
$C_m$
the finite cyclic group
![]() $\textbf{Z}/m\textbf{Z}.$
Recall that
$\textbf{Z}/m\textbf{Z}.$
Recall that
and that
where
![]() $\textbf{A}/\textbf{Q}$
is the ring of adeles of
$\textbf{A}/\textbf{Q}$
is the ring of adeles of
![]() $\textbf{Q}$
and
$\textbf{Q}$
and
![]() $\mathfrak{c}=2^{\aleph_0}$
(see [
Reference BekkaBek23
, proposition 11]).
$\mathfrak{c}=2^{\aleph_0}$
(see [
Reference BekkaBek23
, proposition 11]).
For an integer
![]() $n_0\geq 2,$
let
$n_0\geq 2,$
let
![]() $G= C_{n_0} \wr \textbf{Z}$
be the lamplighter group. We claim that
$G= C_{n_0} \wr \textbf{Z}$
be the lamplighter group. We claim that
and
Indeed, let
![]() $N\,:\!=\,\oplus_{k\in \textbf{Z}}C_{n_0}.$
It will be convenient to describe N as the set of maps
$N\,:\!=\,\oplus_{k\in \textbf{Z}}C_{n_0}.$
It will be convenient to describe N as the set of maps
![]() $f\,:\,\textbf{Z}\to C_{n_0}$
such that
$f\,:\,\textbf{Z}\to C_{n_0}$
such that
![]() ${\rm supp} (\,f)\,:\!=\,\{k\in \textbf{Z} \,:\,f(k)\neq 0\}$
is at most finite. The action of
${\rm supp} (\,f)\,:\!=\,\{k\in \textbf{Z} \,:\,f(k)\neq 0\}$
is at most finite. The action of
![]() $m\in \textbf{Z}$
on
$m\in \textbf{Z}$
on
![]() $f\in N$
is given by translation:
$f\in N$
is given by translation:
![]() $f^m(k)= f(k+m)$
for all
$f^m(k)= f(k+m)$
for all
![]() $k\in \textbf{Z}.$
$k\in \textbf{Z}.$
We identify
![]() $\widehat{C_{n_0} }$
with the group
$\widehat{C_{n_0} }$
with the group
![]() $\mu_{n_0}$
of
$\mu_{n_0}$
of
![]() $n_0$
-th roots of unity in
$n_0$
-th roots of unity in
![]() $\textbf{C}$
by means of the duality
$\textbf{C}$
by means of the duality
Then
![]() $\widehat{N}$
can be identified with the set of maps
$\widehat{N}$
can be identified with the set of maps
![]() $\Phi\,:\,\textbf{Z}\to \mu_{n_0},$
with duality given by
$\Phi\,:\,\textbf{Z}\to \mu_{n_0},$
with duality given by
Observe that
![]() $\Phi(N) \subset \mu_{n_0}$
and so
$\Phi(N) \subset \mu_{n_0}$
and so
![]() $\widehat{N}=\widehat{N}_{\rm finite}.$
$\widehat{N}=\widehat{N}_{\rm finite}.$
We have
![]() $\widehat{N}^{H-{\rm per}}=\bigcup_{m\geq 1}\widehat{N}(m),$
where
$\widehat{N}^{H-{\rm per}}=\bigcup_{m\geq 1}\widehat{N}(m),$
where
![]() $\widehat{N}(m)$
is the subgroup
$\widehat{N}(m)$
is the subgroup
Observe that we have natural injections
![]() $i_{m_2}^{m_1}\,:\,\widehat{N}(m_2) \to \widehat{N}(m_1)$
if
$i_{m_2}^{m_1}\,:\,\widehat{N}(m_2) \to \widehat{N}(m_1)$
if
![]() $m_1$
is a multiple of
$m_1$
is a multiple of
![]() $m_2.$
The dual group A(m) of
$m_2.$
The dual group A(m) of
![]() $\widehat{N}(m)$
can be identified with the set of maps
$\widehat{N}(m)$
can be identified with the set of maps
![]() $\overline{f}\,:\,C_m\to C_{n_0}$
by means of the duality
$\overline{f}\,:\,C_m\to C_{n_0}$
by means of the duality
If
![]() $m_1$
is a multiple of
$m_1$
is a multiple of
![]() $m_2,$
we have a projection
$m_2,$
we have a projection
![]() $p_{m_1}^{m_2}\,:\,A(m_1) \to A(m_2)$
given by
$p_{m_1}^{m_2}\,:\,A(m_1) \to A(m_2)$
given by
The dual group A of
![]() $\widehat{N}^{H-{\rm per}}=\bigcup_{m\geq 1}\widehat{N}(m)$
can then be identified with the projective limit
$\widehat{N}^{H-{\rm per}}=\bigcup_{m\geq 1}\widehat{N}(m)$
can then be identified with the projective limit
![]() $\varprojlim_{m} A(m)$
.
$\varprojlim_{m} A(m)$
.
The action of
![]() $ \textbf{Z}$
by automorphisms of A is given, for
$ \textbf{Z}$
by automorphisms of A is given, for
![]() $r\in \textbf{Z}$
and
$r\in \textbf{Z}$
and
![]() $\overline{f}=(\overline{f}_m)_{m\geq 1}\in A$
by
$\overline{f}=(\overline{f}_m)_{m\geq 1}\in A$
by
![]() $(\overline{f})^r= (\overline{g}_m)_{m\geq 1},$
where
$(\overline{f})^r= (\overline{g}_m)_{m\geq 1},$
where
This action extends to an action of
![]() ${{\rm Proj}}(\textbf{Z}) = {\varprojlim}_m C_m$
by automorphisms on A in an obvious way. By Corollary D, the group
${{\rm Proj}}(\textbf{Z}) = {\varprojlim}_m C_m$
by automorphisms on A in an obvious way. By Corollary D, the group
![]() ${\rm Prof}(G)$
is isomorphic to the corresponding semi-direct product
${\rm Prof}(G)$
is isomorphic to the corresponding semi-direct product
![]() $A \rtimes {\rm Prof} (\textbf{Z})$
and hence
$A \rtimes {\rm Prof} (\textbf{Z})$
and hence
By Corollary D again, the action of
![]() $\textbf{Z}$
on A extends to an action by automorphisms of
$\textbf{Z}$
on A extends to an action by automorphisms of
![]() ${\rm Bohr}(\textbf{Z}).$
Since
${\rm Bohr}(\textbf{Z}).$
Since
![]() ${\rm Bohr}(\textbf{Z})_0$
is connected and A is totally disconnected,
${\rm Bohr}(\textbf{Z})_0$
is connected and A is totally disconnected,
![]() ${\rm Bohr}(\textbf{Z})_0$
acts as the identity on A. Since
${\rm Bohr}(\textbf{Z})_0$
acts as the identity on A. Since
![]() ${\rm Bohr}(\textbf{Z})\cong {\rm Bohr}(\textbf{Z})_0 \times {\rm Prof}(\textbf{Z}),$
it follows that
${\rm Bohr}(\textbf{Z})\cong {\rm Bohr}(\textbf{Z})_0 \times {\rm Prof}(\textbf{Z}),$
it follows that
For another description of
![]() ${\rm Prof}(G),$
see [
Reference Grigorchuk and KravchenkoGK14
, lemma 3·24].
${\rm Prof}(G),$
see [
Reference Grigorchuk and KravchenkoGK14
, lemma 3·24].
5·2. Heisenberg group
Let R be a commutative unital ring. The Heisenberg group is the group
 \begin{equation*} H(R)\,:\!=\,\left\{ \left( \begin{array}{ccc} 1&a&c\\ 0&1&b\\0&0&1 \end{array}\right)\,:\,a,b, c\in R \right\}.\end{equation*}
\begin{equation*} H(R)\,:\!=\,\left\{ \left( \begin{array}{ccc} 1&a&c\\ 0&1&b\\0&0&1 \end{array}\right)\,:\,a,b, c\in R \right\}.\end{equation*}
We can and will identify H(R) with
![]() $R^3$
, equipped with the group law
$R^3$
, equipped with the group law
We will equip R with the discrete topology; in the sequel,
![]() ${\rm Bohr}(R), {\rm Prof}(R),$
and
${\rm Bohr}(R), {\rm Prof}(R),$
and
![]() $\widehat{R}$
will be the Bohr compactification, the profinite completion, and the dual group of
$\widehat{R}$
will be the Bohr compactification, the profinite completion, and the dual group of
![]() $(R, +)$
, the additive group of R.
$(R, +)$
, the additive group of R.
Let
![]() $ {\mathcal I}_{\rm finite}$
be the family of ideals of the ring R with finite index (as subgroups of
$ {\mathcal I}_{\rm finite}$
be the family of ideals of the ring R with finite index (as subgroups of
![]() $(R,+)$
). Every ideal I from
$(R,+)$
). Every ideal I from
![]() ${\mathcal I}_{\rm finite}$
defines two compact groups
${\mathcal I}_{\rm finite}$
defines two compact groups
![]() $H({\rm Bohr}(R), I)$
and
$H({\rm Bohr}(R), I)$
and
![]() $H({\rm Prof}(R), I)$
of Heisenberg type as follows:
$H({\rm Prof}(R), I)$
of Heisenberg type as follows:
is equipped with the group law
where
![]() $p_I\,:\,{\rm Bohr}(R)\to R/I$
is the group homomorphism induced by the canonical map
$p_I\,:\,{\rm Bohr}(R)\to R/I$
is the group homomorphism induced by the canonical map
![]() $R\to R/I;$
the group
$R\to R/I;$
the group
![]() $H({\rm Prof}(R),I)$
is defined in a similar way.
$H({\rm Prof}(R),I)$
is defined in a similar way.
Observe that, for two ideals I and J in
![]() ${\mathcal I}_{\rm finite}$
with
${\mathcal I}_{\rm finite}$
with
![]() $J\subset I,$
we have natural epimorphisms
$J\subset I,$
we have natural epimorphisms
We claim that the canonical maps
![]() $H(R)\to H({\rm Bohr}(R),I)$
and
$H(R)\to H({\rm Bohr}(R),I)$
and
![]() $H(R)\to H({\rm Prof}(R),I)$
induce isomorphisms
$H(R)\to H({\rm Prof}(R),I)$
induce isomorphisms
and
where I runs over
![]() $ {\mathcal I}_{\rm finite}.$
$ {\mathcal I}_{\rm finite}.$
Indeed, H(R) is a semi-direct product
![]() $N\rtimes H$
for
$N\rtimes H$
for
and
Let
![]() $\chi\in \widehat{N}$
. Then
$\chi\in \widehat{N}$
. Then
![]() $\chi = \chi_{\beta, \psi}$
for a unique pair
$\chi = \chi_{\beta, \psi}$
for a unique pair
![]() $(\beta, \psi) \in (\widehat R)^2$
, where
$(\beta, \psi) \in (\widehat R)^2$
, where
![]() $\chi_{\beta, \psi}$
is defined by
$\chi_{\beta, \psi}$
is defined by
For
![]() $h = (a,0,0) \in H$
, we have
$h = (a,0,0) \in H$
, we have
where
![]() $\psi^a \in \widehat R$
is defined by
$\psi^a \in \widehat R$
is defined by
![]() $\psi^a(b) = \psi(a^{-1}b)$
for
$\psi^a(b) = \psi(a^{-1}b)$
for
![]() $b \in R$
. It follows that the H-orbit of
$b \in R$
. It follows that the H-orbit of
![]() $\chi_{\beta, \psi}$
is
$\chi_{\beta, \psi}$
is
and that the stabiliser of
![]() $\chi_{\beta, \psi}$
, which only depends on
$\chi_{\beta, \psi}$
, which only depends on
![]() $\psi$
, is
$\psi$
, is
where
![]() $I_\psi$
is the ideal of R defined by
$I_\psi$
is the ideal of R defined by
Let
![]() ${\widehat R}_{\rm per}$
be the subgroup of all
${\widehat R}_{\rm per}$
be the subgroup of all
![]() $\psi \in\widehat R$
which factorises through a quotient
$\psi \in\widehat R$
which factorises through a quotient
![]() $R/I$
for an ideal
$R/I$
for an ideal
![]() $I\in {\mathcal I}_{\rm finite}.$
It follows that
$I\in {\mathcal I}_{\rm finite}.$
It follows that
The dual group of
![]() ${\widehat R}_{\rm per}$
can be identified with
${\widehat R}_{\rm per}$
can be identified with
![]() $ \varprojlim_{I} R/I$
, where I runs over
$ \varprojlim_{I} R/I$
, where I runs over
![]() ${\mathcal I}_{\rm finite}.$
So, the dual group A of
${\mathcal I}_{\rm finite}.$
So, the dual group A of
![]() ${\widehat N}^{H-{\rm per}}$
can be identified with
${\widehat N}^{H-{\rm per}}$
can be identified with
![]() $ \varprojlim_{I} {\rm Bohr}(R) \times (R/I).$
$ \varprojlim_{I} {\rm Bohr}(R) \times (R/I).$
The action of
![]() ${\rm Bohr}(H)\cong {\rm Bohr}(R)$
on every
${\rm Bohr}(H)\cong {\rm Bohr}(R)$
on every
![]() ${\rm Bohr}(R) \times (R/I)$
is given by
${\rm Bohr}(R) \times (R/I)$
is given by
for the natural map
![]() $p_I\,:\,{\rm Bohr}(R)\to R/I$
. This shows that
$p_I\,:\,{\rm Bohr}(R)\to R/I$
. This shows that
Similarly, the dual group B of
![]() ${\widehat N_{\rm finite}}^{H-{\rm per}}$
can be identified with
${\widehat N_{\rm finite}}^{H-{\rm per}}$
can be identified with
![]() $ \varprojlim_{I} {\rm Prof}(R) \times (R/I)$
and we have
$ \varprojlim_{I} {\rm Prof}(R) \times (R/I)$
and we have
Acknowledgments
It is a pleasure to thank P. de la Harpe for helpful comments. Thanks are also due to the referee for useful suggestions.