A model in which countable Fréchet α1-spaces are first countable
Published online by Cambridge University Press: 04 October 2011
Extract
Although this paper is concerned with answering a question in general topology about sequential convergence, the techniques used may be of greater interest to those interested in the structure of filters on ω. A point in a topological space is called an α1-point if whenever 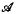 is a countable family of sequences converging to it, there is a sequence B, also converging to it, such that A\B is finite for each A ∈
is a countable family of sequences converging to it, there is a sequence B, also converging to it, such that A\B is finite for each A ∈ 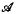 . A space is α1 if each point of the space is an α1-point. Nyikos has shown that the existence of countable Fréchet α1-spaces which are not first countable follows from the assumption
. A space is α1 if each point of the space is an α1-point. Nyikos has shown that the existence of countable Fréchet α1-spaces which are not first countable follows from the assumption 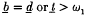 and has asked if it is consistent that no such space exists. It is not difficult to see that if there is an α1-space which is not first countable the there is also one with only one non-isolated point. Since, in answering Nyikos' question, we are only concerned with countable spaces, it follows that we are really dealing with certain types of filters on ω. The precise translation of the topological question to a filter theoretic one is contained in §2. The reader who is not interested in the details may wish to read only §2, the first half of §3 and §5.
and has asked if it is consistent that no such space exists. It is not difficult to see that if there is an α1-space which is not first countable the there is also one with only one non-isolated point. Since, in answering Nyikos' question, we are only concerned with countable spaces, it follows that we are really dealing with certain types of filters on ω. The precise translation of the topological question to a filter theoretic one is contained in §2. The reader who is not interested in the details may wish to read only §2, the first half of §3 and §5.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 105 , Issue 3 , May 1989 , pp. 473 - 480
- Copyright
- Copyright © Cambridge Philosophical Society 1989
References
- 3
- Cited by




