Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-27T04:36:46.023Z Has data issue: false hasContentIssue false
  • English
  • Français

Meridian twisting of closed braids and the Homfly polynomial

Published online by Cambridge University Press:  01 May 2009

TAMÁS KÁLMÁN
TAMÁS KÁLMÁN*
Affiliation:
The University of Tokyo Graduate School of Mathematical Sciences 3-8-1 Komaba, Meguro Tokyo, 153-8914Japan. e-mail: kalman@ms.u-tokyo.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

Let β be a braid on n strands, with exponent sum w. Let Δ be the Garside half-twist braid. We prove that the coefficient of vw−n+1 in the Homfly polynomial of the closure of β agrees with (−1)n−1 times the coefficient of vw+n2−1 in the Homfly polynomial of the closure of βΔ2. This coincidence implies that the lower Morton–Franks–Williams estimate for the v–degree of the Homfly polynomial of 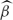is sharp if and only if the upper MFW estimate is sharp for the v–degree of the Homfly polynomial of .

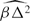Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 146 , Issue 3 , May 2009 , pp. 649 - 660
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bennequin, D.. Entrelacements et équations de Pfaff (French; Links and Pfaffian equations). Astérisque 107–108 (1982), 87–161.Google Scholar
[2]Birman, J. S.. Braids, links and mapping class groups. Annals of Mathematics Studies 82 (Princeton University Press, 1974).Google Scholar
[3]Cha, J. C. and Livingston, C.. KnotInfo: Table of knot invariants. http://www.indiana.edu/knotinfo (2008).Google Scholar
[4]Cromwell, P.. Knots and Links (Cambridge University Press, 2004).CrossRefGoogle Scholar
[5]Dunfield, N. M., Gukov, S., and Rasmussen, J.. The superpolynomial for knot homologies. Experiment. Math. 15 (2006), 129–159.CrossRefGoogle Scholar
[6]Franks, J. and Williams, R. F.. Braids and the Jones polynomial. Trans. Amer. Math. Soc. 303 (1987), 97–108.CrossRefGoogle Scholar
[7]Hoste, J. and Thistlethwaite, M.. Knotscape. Available online at http://www.math.utk.edu/~morwen/knotscape.html/.Google Scholar
[8]Jones, V.. Hecke algebra representations of braid groups and link polynomials. Ann. Math. 126 (1987), 335–388.CrossRefGoogle Scholar
[9]Kálmán, T.. Braid-positive Legendrian links. Int. Math. Res. Not. (2006), Art. ID 14874.Google Scholar
[10]Khovanov, M. and Rozansky, L.. Matrix factorizations and link homology. Fund. Math. 199 (2008), 1–91.CrossRefGoogle Scholar
[11]Morton, H. R.. Seifert circles and knot polynomials. Math. Proc. Camb. Phil. Soc. 99 (1986), 107–109.CrossRefGoogle Scholar
[12]Morton, H. R.. Polynomials from braids. In ‘Braids’, ed. Birman, J. S. and Libgober, A.. Contemp. Math. 78, Amer. Math. Soc. (1988), 375–385.Google Scholar
[13]Rutherford, D.. The Bennequin number, Kauffman polynomial, and ruling invariants of a Legendrian link: the Fuchs conjecture and beyond. Int. Math. Res. Not. (2006), Art. ID 78591.Google Scholar
[14]Wu, H.. Braids, transversal links and the Khovanov–Rozansky theory. Trans. Amer. Math. Soc. 360 (2008), 3365–3389.CrossRefGoogle Scholar
[15]Yokota, Y.. Twisting formulae of the Jones polynomial. Math. Proc. Camb. Phil. Soc. 110 (1991), 473–482.CrossRefGoogle Scholar