1. Introduction
1.1. Background
A ring of positive characteristic has a wealth of objects arising from the Frobenius endomorphism. The focus of this paper are two numerical invariants: Hilbert–Kunz multiplicity and F-signature. For simplicity, let us assume that A is a local domain such that
$A^{1/p}$
is a finitely generated A-module. The Hilbert–Kunz multiplicity of A ([
Reference Kunz27, Reference Monsky30
]) is defined as
\begin{align*}\text{e}_{\text{HK}}(A)\,:\!=\, \lim_{e \to \infty} \dfrac{\mu_A\!\left(A^{1/p^e}\right)}{\operatorname{rank}\!\left(A^{1/p^e}\right)},\end{align*}
where
$\mu_A$
denotes the minimal number of generators, and the F-signature of A ([
Reference Huneke and Leuschke22, Reference Tucker41
]) is
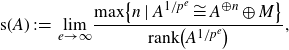\begin{align*}\text{s}(A) \,:\!=\, \displaystyle{\lim_{e \to \infty}} \dfrac{\max\!\left\{n \mid A^{1/p^e} \cong A^{\oplus n} \oplus M\right\}}{\operatorname{rank}\!\left(A^{1/p^e}\right)},\end{align*}
where M is a finitely generated A-module without free direct summands.
A fundamental result of Kunz ([
Reference Kunz26
]) asserts that
$A^{1/p^e}$
is free if and only if A is regular. It follows that
$\text{e}_{\text{HK}}(A) \ge 1$
and
$1 \ge \text{s}(A) \ge 0$
, and under a mild condition the value is 1 if and only if A is regular ([
Reference Huneke and Leuschke22, Reference Kunz26, Reference Watanabe and Yoshida45
]). Furthermore, positivity of F-signature characterises the class of strongly F-regular rings [
Reference Aberbach and Leuschke3
], a fundamental class of mild singularities that first appeared in the tight closure theory [
Reference Hochster and Huneke21
]. A related result of Blickle–Enescu [
Reference Blickle and Enescu4
] shows that small Hilbert–Kunz multiplicity also forces the ring to be strongly F-regular.
A natural question is how close can the Hilbert–Kunz multiplicity of a singularity be to 1? And a natural guess is that the simplest double point singularity
$k[[x_1, \ldots, x_d]]/\left(x_1^2 + \cdots + x_d^2\right)$
should have the smallest Hilbert–Kunz multiplicity (see, Conjecture 2·4 for details). By [
Reference Aberbach and Enescu2, Reference Watanabe and Yoshida46, Reference Watanabe and Yoshida48
] this is now a theorem in dimension at most 6.
In this paper, we extend this investigation by asking to find further bounds on Hilbert–Kunz multiplicity of mild singularities and considering the analogous question for F-signature. For instance, in dimension 2, most non-regular F-regular local rings are quotient singularities, in which case we have that
$\text{s}(A)=1/|G| \le {1}/{2}$
, where
$A=k[[x,y]]^{G}$
and G is a finite subgroup of
$\text{GL}_{2}(k)$
. It seems that a similar question has no answer even in dimension 3.
Question 1·1. Let A be a strongly F-regular local domain of dimension
$d \ge 3$
which is not regular. Then what is the upper bound on
$\text{s}(A)$
?
We give a partial answer to the question above, and pose a conjecture; see Conjecture 2·10. Let us explain the organisation of the paper.
1.2. Structure of the paper and main results
In Section 2, we recall several definitions (Hilbert–Kunz multiplicity, F-regularity, FFRT, F-signature and so on) and pose two conjectures. In Section 3, we give a lower bound on Hilbert–Kunz multiplicities. Namely, we prove the following theorem and its refinement in the 3-dimensional case (see Theorem 3·7).
Theorem 1·2 (see Theorem 3·2). Let
$(A,\mathfrak{m})$
be a formally unmixed local ring of characteristic
$p>0$
. If
${d=\dim A \ge 3}$
, then for every
$\mathfrak{m}$
-primary ideal I we have
\begin{align*}\text{e}_{\text{HK}}(I) > \dfrac{\text{e}(I)+d}{d!}.\end{align*}
In Section 4, we generalise an argument of De Stefani and the first author that
$\text{s}(A) \le {1}/{2}$
for non-Gorenstein Cohen–Macaulay local rings A (see Proposition 4·1) and characterise the case where equality holds.
Theorem 1·3 (see Theorem 4·6). Let A be a Cohen–Macaulay local domain with the canonical module
$\omega_A$
which is not Gorenstein. Then
$\text{s}(A) \le {1}/{2}$
, and the following conditions are equivalent
$:$
-
(i)
$\text{s}(A) = {1}/{2}$
; -
(ii)
$A^{1/p^e}$
is a finite direct sum of A and
$\omega_A$
for every
$e \ge 1$
.
When this is the case,
$\text{e}_{\text{HK}}(A) = ({\text{type}(A)+1})/{2}$
. If, in addition, either A is
$\mathbb{Q}$
-Gorenstein or a toric singularity, then it is isomorphic to the Veronese subring
$k\left[\left[x_1,x_2,\ldots,x_d\right]\right]^{(2)}$
, where
$k[[x_1,\ldots,x_d]]^{(n)}=k[[(x_1,\ldots, x_d)^n]]$
(see Theorem 4·14 and 5·6).
The F-signature of a Gorenstein ring may exceed
${1}/{2}$
. We explore an upper bound on F-signature for Gorenstein, non-regular local rings of dimension three.
Theorem 1·4 (see, Theorem 4·15). Let
$(A,\mathfrak{m},k)$
be a
$3$
-dimensional Gorenstein strongly F-regular local ring with
$\text{e}(A) \ge 3$
. Then
$\text{s}(A) \le {\text{e}(A)}/{24}$
.
We also provide a classification of (pointed, normal, affine) toric rings with F-signature greater than one half.
Theorem 1·5 (see Theorem 5·12). The toric rings with F-signature greater than
$\frac{1}{2}$
are, up to isomorphism, as follows:
-
(i) for a polynomial ring A, we have
$s(A)=1$
; -
(ii) for the coordinate ring A of the Segre product
$\mathbb{P}^1 \# \mathbb{P}^1$
, we have
$s(A)=2/3$
; -
(iii) for the coordinate ring A of the Segre product
$\mathbb{P}^2 \# \mathbb{P}^2$
, we have
$s(A)=11/20$
.
2. Preliminaries
Let
$(A,\mathfrak{m})$
be a local ring of characteristic
$p>0$
and let
$F^e \,:\, A \to A$
denote the
$e{\text{th}}$
iterated Frobenius map of A. For an A-module M, the Frobenius push-forward of M,
$F^{e}_{*}M=\{F^{e}_{*}m \mid m \in M\}$
, is defined as follows: it agrees with M as an abelian group and A acts by
$a \cdot F^{e}_{*}m =F^{e}_{*}(a^{p^e}m)$
for any
$a \in A$
and
$m \in M$
. If A is reduced,
$F^{e}_{*}A$
is identified with
$A^{1/p^e}$
which consists of
$p^e$
-th roots of A. The ring A is called F-finite if
$F^{e}_{*}A$
is a finitely generated A-module for every (some)
$e \ge 1$
.
We now recall a more general definition of Hilbert–Kunz multiplicity.
Definition 2·1. Let
$\ell_A(W)$
denote the length of a finitely generated A-module W. For an
$\mathfrak{m}$
-primary ideal
$I \subset A$
we denote
$I^{[q]}=(a^q \mid a \in I)A$
for each
$q=p^e$
. If M is a finitely generated A-module,
\begin{align*}\text{e}(I, M) \,:\!=\, \lim_{n \to \infty}\, \dfrac{d!}{n^d} \ell_A\!\left(M/I^{n+1}M\right)\quad\left(\text{resp.} \;\text{e}_{\text{HK}}(I, M)\,:\!=\, \lim_{q \to \infty} \dfrac{\ell_A(M/I^{[q]}M)}{q^d}\right)\end{align*}
is called the multiplicity (resp. the Hilbert–Kunz multiplicity) of M with respect to I. For brevity, we denote
$\text{e}(I)=\text{e}(I, A)$
(resp.
$\text{e}_{\text{HK}}(I)=\text{e}_{\text{HK}}(I,A)$
) and call it the multiplicity (resp. the Hilbert–Kunz multiplicity) of I. We also denote,
$\text{e}(\mathfrak{m},M)=\text{e}(M)$
and
$\text{e}_{\text{HK}}(\mathfrak{m}, M)=\text{e}_{\text{HK}}(M)$
.
Recall the fundamental properties of Hilbert–Kunz multiplicities; see e.g. [ Reference Watanabe and Yoshida45 ].
Proposition 2·2 [
Reference Hanes15
], [
Reference Watanabe and Yoshida45
, (2·3),(2·4),(2·5)]. Let
$I \subset A$
be an
$\mathfrak{m}$
-primary ideal.
-
(i) The following inequalities hold true
$:$
If, in addition,
\begin{align*}\dfrac{\text{e}(I)}{d!} \le \text{e}_{\text{HK}}(I) \le \text{e}(I).\end{align*}
$d \ge 3$
, then
${\text{e}(I)}/{d!} < \text{e}_{\text{HK}}(I)$
.
-
(ii) If I is a parameter ideal, then
$\text{e}_{\text{HK}}(I)=\text{e}(I)$
. -
(iii) Let
$\text{Assh}(A)$
denote the set of all associated prime ideals P with
$\dim A/P=\dim A$
. Then
\begin{align*}\text{e}_{\text{HK}}(I,M) = \sum_{P \in \text{Assh}(A)} \text{e}_{\text{HK}}(I, A/P) \cdot \ell_{A_P}(M_P).\end{align*}
2.1. Minimal value of Hilbert–Kunz multiplicity
Now we want to discuss the conjectural lower bound on Hilbert–Kunz multiplicities of singularities. In order to state it, we recall the definition of type
$(A_1)$
simple singularity.
Definition 2·3. Let p be a prime number, k be an algebraically closed field of characteristic p, and d a positive integer. Then we define
$A_{p,d}$
as follows:
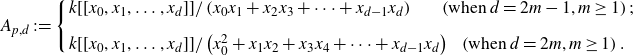\begin{align*}A_{p,d} \,:\!= \left\{\begin{array}{lc}k[[x_0,x_1,\ldots,x_d]]/\left(x_0x_1+x_2x_3+\cdots + x_{d-1}x_d\right) & \!\!\!\left(\text{when}\ d=2m-1, m \ge 1\right); \\[3mm]k[[x_0,x_1,\ldots,x_d]]/\left(x_0^2+x_1x_2+x_3x_4+\cdots + x_{d-1}x_d\right) & \left(\text{when}\ d=2m, m \ge 1\right).\end{array}\right.\end{align*}
For
$p > 2$
the equation takes a more familiar form
$A_{p, d} \cong k[[x_0,x_1,\ldots,x_d]]/(x_0^2+x_1^2+\cdots + x_d^2)$
. Han and Monsky ([
Reference Han and Monsky14
]) gave an algorithm to compute
$\text{e}_{\text{HK}} (A_{p,d})$
given p and d. However, an explicit formula for
$\text{e}_{\text{HK}} (A_{p,d})$
as a function of p is only known for small values of d (see [
Reference Yoshida51
] for examples). Gessel and Monsky ([
Reference Gessel and Monsky12
]) showed that
$\lim_{p \to \infty} \text{e}_{\text{HK}}(A_{p,d}) = 1+ c_d$
where
\begin{align*}\sec x + \tan x = 1 + \sum_{i=1}^{\infty} c_d\, x^d \quad\bigg(|x| < \dfrac{\pi}{2}\bigg).\end{align*}
The first several values of
$c_d$
are recorded in Table 1 below.
Conjecture 2·4 (cf. [
Reference Watanabe and Yoshida48
, conjecture 4·2]). Let
$(A,\mathfrak{m}, k)$
be an F-finite, formally unmixed, non-regular local ring of dimension
$d \geq 1$
. Then:
-
(i)
$\text{e}_{\text{HK}}(A) \ge \text{e}_{\text{HK}}(A_{p,d}) \ge 1+ c_d$
, where
$c_d$
is defined above; -
(ii) Suppose that
$k=\overline{k}$
. If
$\text{e}_{\text{HK}}(A)=\text{e}_{\text{HK}}(A_{p,d})$
, then
$\widehat{A} \cong A_{p,d}$
.
Let us summarise the cases where Conjecture 2·4 is known.
Theorem 2·5. Let A be a formally unmixed, non-regular local ring and p be an odd prime number.
-
(i) If
$d \leq 3$
then Conjecture 2·4 holds and
$\text{e}_{\text{HK}}(A_{p, d}) = 1 + c_d$
([
Reference Watanabe and Yoshida46
, theorem 3·1], [
Reference Watanabe and Yoshida48
, theorem 3·1]). In fact, these results also show that
$\text{e}_{\text{HK}}(A) \ge \text{e}_{\text{HK}}(A_{p,d}) = 1+ c_d$
for
$p = 2$
. -
(ii) If
$d=4$
, then Conjecture 2·4 holds ([
Reference Watanabe and Yoshida48
, theorem 4·3]) but
$\text{e}_{\text{HK}}(A_{p,4})= ({29p^2+15})/({24p^2+12}) > {29}/{24}$
now depends on p ([
Reference Gessel and Monsky12
]). -
(iii) If
$d = 5,6$
then
$\text{e}_{\text{HK}}(A) \ge \text{e}_{\text{HK}}(A_{p,d}) \ge 1 + c_d$
([
Reference Aberbach and Enescu2
, theorem 5·2]). -
(iv) If A is a complete intersection local ring, then
$\text{e}_{\text{HK}}(A) \ge \text{e}_{\text{HK}}(A_{p,d})$
(see [
Reference Enescu and Shimomoto10
, theorem 4·6]). -
(v) The inequality
$\text{e}_{\text{HK}}(A_{p,d}) \ge 1+ c_d$
in full generality appears in the recent preprint of Trivedi [
Reference Trivedi40
]. -
(vi) Yoshida [ Reference Yoshida51 ] conjectures that
$\text{e}_{\text{HK}}(A_{p,d})$
is a decreasing function in p for a fixed d. For p sufficiently large (depending on d) Yoshida’s conjecture is also asserted by Trivedi in [
Reference Trivedi40
].
Observation 2·6. If
$p=2$
and
$d=2m$
$(m=1,2,\ldots)$
, then the following statement can be proved by using an argument in [
Reference Han and Monsky14
] (see [
Reference Yoshida51
] for details)
\begin{align*}\ell \!\left(A_{2,d}/\mathfrak{m}^{[2^e]}\right) = \dfrac{2^m+1}{2^m} \; 2^{de}.\end{align*}
In particular,
$\text{e}_{\text{HK}}(A_{2,d})= ({2^m+1})/{2^m}$
.
Similarly, [
Reference Yoshida51
] conjectures that if
$d=2m-1$
$(m=1,2,\ldots)$
, then
\begin{align*}\ell \!\left(A_{2,d}/\mathfrak{m}^{[2^e]}\right) = \frac{2^m}{2^m-1}\;2^{de} - \dfrac{\left(2^{m-1}\right)^e}{2^m-1}\end{align*}
for every
$e \ge 1$
. In particular, if would follow that
$\text{e}_{\text{HK}}(A_{2,d})={2^m}/({2^m-1}).$
Based upon these observations, we pose an improved conjecture as follows:
Conjecture 2·7. Let
$(A,\mathfrak{m}, k)$
be a formally unmixed non-regular local ring of dimension
$d \ge 1$
and with algebraically closed residue field. Let
$m \geq 1$
be an integer.
-
(i) If
$d=2m-1$
, then either
$\widehat{A} \cong A_{p,d}$
or
$\text{e}_{\text{HK}}(A) > {2^m}/({2^m-1})$
. -
(ii) If
$d=2m$
, then either
$\widehat{A} \cong A_{p,d}$
or
$\text{e}_{\text{HK}}(A) > ({2^m+1})/{2^m}$
.
By results of Watanabe and Yoshida, Conjecture 2·7 has an affirmative answer when
$p \ge 3$
and
$d \le 4$
. The following table depicts the difference between two conjectures.
Table 1. Comparison between the two conjectured bounds
2.2. Strong F-regularity and F-signature
Hilbert–Kunz multiplicity is inherently connected with tight closure, a powerful theory developed by Hochster and Huneke in a series of papers starting at [ Reference Hochster and Huneke20 ].
Definition 2·8 (cf. [
Reference Hochster and Huneke20
]) Let
$I \subset A$
be an ideal, and let x be an element of A. Put
$A^{o}=A \setminus \cup_{P \in \text{Min}(A)} P$
. For
$x \in A$
, we say that x is in the tight closure of I (denoted by
$I^{*}$
) if there exists an element
$c \in A^{o}$
such that
$cx^q \in I^{[q]}$
for sufficiently large
$q=p^e$
.
A local ring A is said to be weakly F-regular (resp. F-rational) if any ideal I (resp. any parameter ideal I) is tightly closed, that is,
$I^{*}=I$
.
A result of Hochster and Huneke [
Reference Hochster and Huneke20
, theorem 8·17] asserts that
$\text{e}_{\text{HK}}(I^*) = \text{e}_{\text{HK}}(I)$
and, moreover,
$I^*$
is the largest ideal containing I with same Hilbert–Kunz multiplicity.
On the other hand, F-signature coincides with the minimal relative Hilbert–Kunz multiplicity [ Reference Polstra and Tucker32, Reference Watanabe and Yoshida47, Reference Yao50 ] and is connected to the following class of singularities.
Definition 2·9 (cf. [
Reference Hochster and Huneke21
]). An F-finite local ring A is called strongly F-regular if for any
$c \in A^{o}$
, there exists
$q = p^e$
,
$e \ge 1$
such that the map
$A \hookrightarrow A^{1/q}$
defined by
$x \mapsto c^{1/q}x$
splits as an A-linear map. Any Noetherian ring A is called strongly F-regular if any localization of A is also a strongly F-regular local ring.
Strongly F-regular singularities enjoy many nice properties and are always normal and Cohen-Macaulay. For example, quotient singularities and toric singularities are strongly F-regular rings. As it was already mentioned,
$\text{s}(A) > 0$
if and only if A is strongly F-regular by a result of Aberbach and Leuschke [
Reference Aberbach and Leuschke3
, theorem 0·2]. The two notions of F-regularity are conjectured to be equivalent and are known to be equivalent in several cases, such as Gorenstein rings [
Reference Hochster and Huneke19
].
The simple singularity
$A_{p,d}$
discussed above is a hypersurface with
$\text{e}(A_{p,d})=2$
, thus by [
Reference Watanabe and Yoshida47
, example 2·3]
$\text{e}_{\text{HK}}(A)=2-\text{s}(A)$
and
$\text{s}(A)$
attains the maximal value if and only if
$\text{e}_{\text{HK}}(A)$
is minimal. The following conjecture is then natural.
Conjecture 2·10. Let
$(A,\mathfrak{m})$
be a non-regular local ring of dimension
$d \geq 1$
. Then
\begin{align*}\text{s}(A)\le 2-\text{e}_{\text{HK}}(A_{p,d}) = \text{s}(A_{p,d}).\end{align*}
The theory of F-signature originates in the following particular case of rings of finite F-representation type, which was introduced by Smith and Van den Bergh [ Reference Smith and Van den Bergh37 ] (see also [ Reference Yao49 ]).
Definition 2·11. We say that A has finite F-representation type (FFRT) if there is a finite set
$\mathcal{S}=\{M_0,M_1,\ldots,M_n \}$
of isomorphism classes of indecomposable finitely generated A-modules such that for any positive integer e,
$F_{*}^eA$
is isomorphic to a finite direct sum of these modules, that is,
\begin{align*}F_{*}^eA \cong M_0^{\oplus c_{0,e}} \oplus M_1^{\oplus c_{1,e}}\oplus \cdots \oplus M_n^{\oplus c_{n,e}}\end{align*}
for some
$c_{i,e} \in \mathbb{Z}_{\ge 0}$
. Moreover, we say that a finite set
$\mathcal{S}=\{M_0,M_1,\ldots,M_n\}$
as above is the (FFRT) system of A if every A-module
$M_i$
appears non-trivially in
$F_{*}^eA$
as a direct summand for some
$e \in \mathbb{N}$
.
3. Lower bound on Hilbert–Kunz multiplicities
The last two authors gave a lower bound on Hilbert–Kunz multiplicities of two-dimensional unmixed (Cohen–Macaulay) local rings A in terms of usual multiplicities:
\begin{align*}\text{e}_{\text{HK}}(I) \ge \dfrac{\text{e}(I)+1}{2}\end{align*}
for any
$\mathfrak{m}$
-primary ideal I of A [
Reference Watanabe and Yoshida46
]. In this section, we consider a higher dimensional analogue of this inequality; see Theorem 3·2.
We recall [
Reference Aberbach and Enescu2
, theorem 3·2] which improves the volume estimation technique developed in [
Reference Watanabe and Yoshida48
]. For any real number s we define
$v_{s,d}$
to be the volume of
$\{(x_1, \ldots, x_d) \in [0,1]^d \mid \sum_{i = 1}^d x_i \leq s\}$
which can be computed as
\begin{align*}v_{s,d} = \sum_{n = 0}^{\lfloor s \rfloor}({-}1)^n \frac{(s - n)^d}{(d-n)!\ n!},\end{align*}
where
$\lfloor \quad \rfloor$
stands for round down.
For an element
$x \in A$
we denote
\begin{align*}\overline{\nu}_I(x) \,:\!=\, \lim_{n \to \infty} \frac{\sup\!\left\{k \mid x^n \in I^k\right\}}{n}.\end{align*}
It is known that the limit exists and
$\overline{\nu}_I(x) \geq k$
if and only if
$x \in \overline{I^k}$
; see Rees [
Reference Rees34
].
Theorem 3·1 (Aberbach–Enescu [
Reference Aberbach and Enescu2
]). Let
$(A, \mathfrak{m})$
be a formally unmixed reduced local ring of characteristic
$p > 0$
and dimension d. Let J be a minimal reduction of an
$\mathfrak{m}$
-primary ideal I and let r be an integer such that
$r \geq \mu_A(I/J^*)$
. For every real number
$s \geq 0$
, we have
\begin{align*}\text{e}_{\text{HK}}(I) \geq \text{e}(I) \bigg(v_{s,d} - \sum_{i = 1}^r v_{s - t_i,d} \bigg),\end{align*}
where
$t_i = \overline{\nu}_I(z_i)$
for
$z_1, \ldots, z_r$
generators of I modulo
$J^{*}$
.
In particular,
\begin{align*}\text{e}_{\text{HK}}(I) \geq \text{e}(I) \!\left(v_{s,d} - r\cdot v_{s - 1,d} \right).\end{align*}
Using the above theorem and the technique developed in [ Reference Aberbach and Enescu1 ], we can improve Proposition 2·2.
Theorem 3·2. Let
$(A,\mathfrak{m})$
be a formally unmixed local ring of characteristic
$p>0$
. If
$d=\dim A \ge 3$
, then for every
$\mathfrak{m}$
-primary ideal I we have
\begin{align*}\text{e}_{\text{HK}}(I) > \dfrac{\text{e}(I)+d}{d!}.\end{align*}
Definition 3·3. A Cohen–Macaulay local ring
$(A, \mathfrak{m})$
is said to have minimal multiplicity if
$\mu_A(\mathfrak{m})=\text{e}(A)+\dim A-1$
. This condition is equivalent to requiring that
$\mathfrak{m}$
is stable, that is,
$\mathfrak{m}^2=J\mathfrak{m}$
for some minimal reduction J of
$\mathfrak{m}$
.
In what follows, we may assume that A is complete and the residue field
$k=A/\mathfrak{m}$
is infinite since such extensions do not affect multiplicity and Hilbert–Kunz multiplicity.
Lemma 3·4. Let
$(A,\mathfrak{m},k)$
be a formally unmixed local ring of characteristic
$p>0$
. Let I denote an
$\mathfrak{m}$
-primary ideal and J its minimal reduction. Then
$\mu_A(I/J^{*}) \le \text{e}(I)-1$
. Moreover, the equality holds if and only if
$I = \mathfrak{m}$
and
$\widehat{A}$
is F-rational and has minimal multiplicity.
Proof. By definition,
$\mu_A(I/J^{*}) =\ell_A(I/J^{*}+\mathfrak{m} I)$
. Thus, by colon-capturing (see for example [
Reference Ma, Hung Quy and Smirnov29
, lemma 4 and proof of theorem 6]),
\begin{equation}\mu_A(I/J^{*}) = \ell_A(A/J^{*}) - \ell_A(A/I) - \ell_A(\mathfrak{m} I/J^*\cap\mathfrak{m} I)\le \text{e}(I) - 1 - \ell_A(\mathfrak{m} I/J^*\cap\mathfrak{m} I),\end{equation}
and the first assertion follows.
For the second assertion we recall that the equality
$\text{e}(J) = \ell_A (A/J^*)$
for some parameter ideal characterises F-rationality by a theorem of Goto and Nakamura [
Reference Goto and Nakamura13
]. Hence, the equality in (3·1) forces A to be F-rational and
$I = \mathfrak{m}$
. However, for
$\mu_A(I/J^{*}) = \text{e}(I) - 1$
we additionally need that
$\ell_A(\mathfrak{m} I/J^*\cap\mathfrak{m} I) = 0$
, i.e.,
$\mathfrak{m}^2 \subseteq J$
. Since J is a minimal reduction,
$\mathfrak{m}^2 \cap J = \mathfrak{m} J$
, so this condition is equivalent to minimal multiplicity. Note that a complete F-rational ring is necessarily Cohen–Macaulay.
The following proposition gives a refinement of Aberbach and Enescu [ Reference Aberbach and Enescu1 , corollary 3·4].
Proposition 3·5. Let
$(A,\mathfrak{m})$
be a Cohen-Macaulay local ring of dimension
$d \ge 1$
. Let I be an
$\mathfrak{m}$
-primary ideal and suppose that there exists a minimal reduction J of I such that
$I^2 \subset J$
(e.g. I is stable). Then
\begin{align*}\text{e}_{\text{HK}}(I) \ge \dfrac{\text{e}(I)}{2}.\end{align*}
Proof. Let
$\omega_A$
denote the canonical module of A. First we observe that
$\text{e}_{\text{HK}}(J, \omega_A) = \text{e}_{\text{HK}}(J)$
for any
$\mathfrak{m}$
-primary ideal J. Namely, we use Proposition 2·2(iii) after noting that
$\ell_A ((\omega_A)_P) = \ell_A (\omega_{A_P}) = \ell_A (A_P)$
, by the Matlis duality in the artinian ring
$A_P$
.
Since
$I^{[q]}\omega_A \subseteq J^{[q]} \omega_A \,:\, I^{[q]}$
for any
$q=p^e$
by assumption, we get
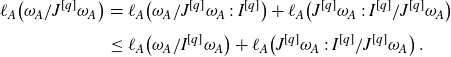\begin{eqnarray*}\ell_A\!\left(\omega_A/J^{[q]}\omega_A\right)&=& \ell_A\!\left(\omega_A/J^{[q]}\omega_A \,:\, I^{[q]}\right)+\ell_A\!\left(J^{[q]}\omega_A \,:\, I^{[q]}/J^{[q]}\omega_A\right) \\[4pt]&\le & \ell_A\!\left(\omega_A/I^{[q]}\omega_A\right) +\ell_A\!\left(J^{[q]}\omega_A \,:\, I^{[q]}/J^{[q]}\omega_A\right).\end{eqnarray*}
Then we compute
$\lim\limits_{q\to\infty} \dfrac{\ell_A\!\left(\omega_A/I^{[q]}\omega_A\right)}{q^d}=\text{e}_{\text{HK}}\!\left(I, \omega_A\right)=\text{e}_{\text{HK}}(I)$
and
\begin{align*}\lim_{q\to\infty} \dfrac{\ell_A\!\left(\omega_A/J^{[q]}\omega_A\right)}{q^d}=\text{e}_{\text{HK}}\!\left(J, \omega_A\right)=\text{e}_{\text{HK}}(J)=\text{e}(I).\end{align*}
On the other hand, since
\begin{align*}\frac{\left(J^{[q]}\omega_A \,:\, I^{[q]}\right)}{J^{[q]}\omega_A} \cong \text{Hom}_{A/J^{[q]}}\!\left(A/I^{[q]}, \omega_A/J^{[q]}\omega_A\right) \cong \text{Hom}_{A/J^{[q]}}\!\left(A/I^{[q]}, \omega_{A/J^{[q]}}\right) \cong \omega_{A/I^{[q]}},\end{align*}
we get that
$\ell_A\!\left(\left(J^{[q]}\omega_A \,:\, I^{[q]}\right)/J^{[q]}\omega_A\right)= \ell_A\!\left(\omega_{A/I^{[q]}}\right)=\ell_A\!\left(A/I^{[q]}\right)$
by the Matlis duality. Hence
\begin{align*}\lim_{q\to\infty}\dfrac{\ell_A\!\left(\left(J^{[q]}\omega_A \,:\, I^{[q]}\right)/J^{[q]}\omega_A\right)}{q^d}=\text{e}_{\text{HK}}(I)\end{align*}
and thus
$\text{e}(I) \le 2 \cdot \text{e}_{\text{HK}}(I)$
, as required.
Corollary 3·6. ([
Reference Aberbach and Enescu1
]). Let A be a Cohen–Macaulay local ring of dimension d with minimal multiplicity. Then
$\text{e}_{\text{HK}}(A) \ge {\text{e}(A)}/{2}$
.
Proof of Theorem 3·2. We may assume that I is tightly closed because
$\text{e}_{\text{HK}}(I)=\text{e}_{\text{HK}}(I^{*})$
and
$\text{e}(I)=\text{e}(I^{*})$
. Moreover, we may assume
$\text{e}(I) \ge 2$
. Let J be a minimal reduction of I.
Case 1. The case where A is F-rational and
$I^2 \subset J$
.
We can apply Proposition 3·5 to obtain
$\text{e}_{\text{HK}}(I) \ge \dfrac{\text{e}(I)}{2} > \dfrac{\text{e}(I)+d}{d!}$
if
$d \ge 3$
and
$\text{e}(I) \ge 2$
.
Case 2. The remaining case where either
$I^2 \not \subset J$
or A is not F-rational.
By Lemma 3·4, we have
$\mu_A(I/J^{*}) \le \text{e}(I)-2$
. So we can apply Theorem 3·1 as
$\text{e}=\text{e}(I) \ge 2$
,
$r=\text{e}-2$
and
$s=1+ {1}/{\text{e}}$
. Then
$\lfloor s \rfloor =1$
and
\begin{eqnarray*}d! \cdot \text{e}^d \!\left(v_{s, d}-r \cdot v_{s-1, d}\right)&=& \text{e}^d \cdot d! \cdot \left(\dfrac{(1+1/\text{e})^d}{d!}- \dfrac{(1/\text{e})^d}{(d-1)!}-(\text{e}-2) \dfrac{(1/\text{e})^d}{d!} \right ) \\[1mm]&=& (\text{e}+1)^d - d -\text{e}+2 \\[1mm]&=& \text{e}^d+d\text{e}^{d-1}+\sum_{k=2}^{d-2} \!\left(\begin{array}{c}d\\k\end{array}\right) \text{e}^k+ d\text{e}+1 -d-\text{e}+2 \\[1mm]&\ge & \text{e}^d + d\text{e}^{d-1}+(d-1)(\text{e}-1)+2 \gt \text{e}^{d-1}(\text{e}+d).\end{eqnarray*}
Hence
$\text{e}_{\text{HK}}(I) \ge \text{e}(v_{s,d}-r\cdot v_{s-1, d})> ({\text{e}+d})/{d!}$
, as required.
If we fix d, then this is not the best possible. In this paper, we prove the following theorem, which gives the optimal bound on the Hilbert–Kunz multiplicity
$\text{e}_{\text{HK}}(A)$
in dimension 3.
Theorem 3·7. Let
$(A,\mathfrak{m},k)$
be a formally unmixed local ring of dimension 3 and characteristic
$p>0$
. Then
\begin{align*}\text{e}_{\text{HK}}(A) \ge \frac{\text{e}(A)}{6}+1.\end{align*}
If equality holds, then A is a strongly F-regular local ring with
$\text{e}(A)=2$
. Moreover, if, in addition, the residue field k is algebraically closed and
$p \ge 3$
, then
$\widehat{A} \cong k[[x,y,z,w]]/(xz-yw)$
and
$\text{e}_{\text{HK}}(A)={4}/{3}$
.
In order to prove the theorem, we prove a stronger result as follows.
Lemma 3·8. Under the assumptions of Theorem 3·7, we suppose that
$\text{e} =\text{e}(A) \ge 3$
. If R is F-rational with minimal multiplicity then
$\text{e}_{\text{HK}}(A) \ge \dfrac{\text{e}}{6}\left({\text{e}+2+\sqrt{\text{e}+2}})/({\text{e}+1}\right)^2$
. If one of these conditions does not hold, then we have a stronger bound
\begin{align*}\text{e}_{\text{HK}}(A) \ge\dfrac{ 1 }{6}\left(\text{e}+3+\frac{ 2 }{\text{e}}+\left(2+\frac{2}{\text{e}}\right)\sqrt{\text{e}+1} \right).\end{align*}
Proof. We will optimise the volume estimate from Theorem 3·1 and we use Lemma 3·4 to get a bound on
$r = \mu_A(I/J^{*})$
.
We now start with the first inequality. For
$1 \le s \le 2$
, by Theorem 3·1
\begin{eqnarray*}\text{e}_{\text{HK}}(A) & \ge & \text{e} \cdot \left(v_{s,3}-(\text{e}-1)v_{s-1,3}\right)\\&=&\text{e} \cdot \left (\dfrac{s^3}{6}-\dfrac{(s-1)^3}{2}-(\text{e}-1)\dfrac{(s-1)^3}{6}\right ) \\[1mm]&=&\dfrac{\text{e} \!\left(s^3-(\text{e}+2)(s-1)^3\right)}{6}.\end{eqnarray*}
We consider a function
$f(s)=s^3-(\text{e}+2)(s-1)^3$
. The derivative is given by
$f^{\prime}(s)=3s^2-3(\text{e}+2)(s-1)^2$
and the equation
$f^{\prime}(s)=0$
has roots
$s_{\pm}=\left({\text{e}+2\pm \sqrt{\text{e}+2}}\right)/({\text{e}+1})$
. Since
$s_{-} < 1 < s_{+} < 2$
, the maximum on
$1 \le s \le 2$
is at
$s_{+}$
which gives the inequality:
\begin{align*}\text{e}_{\text{HK}}(A) \ge \frac{\text{e}}{6} \cdot f(s_{+})=\dfrac{\text{e}}{6}\cdot s_{+}^2=\dfrac{\text{e}}{6}\left(\dfrac{\text{e}+2+\sqrt{\text{e}+2}}{\text{e}+1}\right)^2.\end{align*}
In the second case, we may estimate that
$\text{e}_{\text{HK}}(A) \ge \text{e} \cdot (v_{s, 3}-(\text{e}-2)v_{s-1, 3})$
and
$\text{e} \ge 3$
. So if we consider
$g(s)=s^3-(\text{e}+1)(s-1)^3$
, then
$1 \le \left({\text{e}+1+\sqrt{\text{e}+1}}\right)/{\text{e}} \le 2$
and a similar argument as above implies
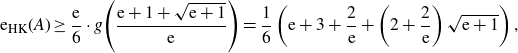\begin{align*}\text{e}_{\text{HK}}(A) \ge \dfrac{\text{e}}{6}\cdot g\!\left({\dfrac{\text{e}+1+\sqrt{\text{e}+1}}{\text{e}}}\right)=\dfrac{1}{6}\left(\text{e}+3+\frac{2}{\text{e}}+\left(2+\frac{2}{\text{e}}\right)\sqrt{\text{e}+1} \right),\end{align*}
as required.
Proof of Theorem 3·7. First suppose that A is neither F-rational nor Cohen–Macaulay with minimal multiplicity. If
$\text{e}=2$
, then
$\text{e}_{\text{HK}}(A)=2 > {4}/{3} = {\text{e}}/{6}+1$
. Hence we may assume
$\text{e} =\text{e}(A) \ge 3$
. Then Lemma 3·8 yields that
\begin{align*}\text{e}_{\text{HK}}(A) \ge \dfrac{1}{6}\left(\text{e}+3+\frac{ 2 }{\text{e}}+\left(2+\frac{2}{\text{e}}\right)\sqrt{\text{e}+1} \right) > \dfrac{\text{e}}{6}+1.\end{align*}
Next suppose that A is F-rational and Cohen–Macaulay with minimal multiplicity.
If
$\text{e} \ge 4$
, then
$\text{e}_{\text{HK}}(A) \ge {\text{e}}/{2} > {\text{e}}/{6}+1$
.
If
$\text{e}=3$
, then [
Reference Watanabe and Yoshida48
, lemma 3·3(3)] implies
$\text{e}_{\text{HK}}(A) \ge {13}/{8} > {3}/{2} = {\text{e}}/{6}+1$
.
Suppose that
$\text{e}=2$
. Then the main theorem in [
Reference Watanabe and Yoshida48
] yields
$\text{e}_{\text{HK}}(A) \ge {4}/{3} = {\text{e}}/{6}+1$
and equality holds if and only if
$\widehat{A} \cong k[[x,y,z,w]]/(xz-yw)$
. Therefore we complete the proof.
4. Upper bounds on F-signature
The main aim of this section is to give an upper bound on F-signature for non-Gorenstein Cohen–Macaulay local rings. We start with a few preliminaries.
We say that M is a maximal Cohen–Macaulay A-module if it is a finitely generated R-module such that any (equiv., some) system of parameters of R is an M-regular sequence. For such modules
$\mu_A(M) \le \text{e}(M)$
, because multiplicity can be computed from a regular sequence. We say that M is an Ulrich A-module if
$\mu_A(M)=\text{e}(M)$
. Ulrich modules first appeared in [
Reference Brennan5
] under the name maximally generated maximal Cohen–Macaulay module.
If A is a local ring of positive characteristic
$p > 0$
and M is a finitely generated A-module then the rank of the largest free summand of M is independent of a decomposition, because we may pass to the completion, see [
Reference Polstra and Smirnov31
, remark 3·4]. Moreover, if A is a Cohen–Macaulay local ring with the canonical module
$\omega_A$
and M is maximal Cohen–Macaulay, then the number of direct summand of M isomorphic to
$\omega_A$
is also independent of a direct decomposition, since these correspond to a free summand of
$\text{Hom}_A (M, \omega_A)$
. Last, we note that an F-finite Cohen–Macaulay ring has a canonical module by a result of Gabber [
Reference Gabber11
, remark 13·6].
The following proposition is related to lemma 3·1 of [
Reference Ma, Polstra, Schwede and Tucker28
]; the second assertion was initially observed by De Stefani and Jeffries in relation with Sannai’s dual F-signature ([
Reference Sannai35
]). Recall that
$\text{type}(A)$
is the minimal number of generators of
$\omega_A$
.
Proposition 4·1. Let A be an F-finite Cohen–Macaulay local domain which is not Gorenstein. Then
\begin{align*}\text{e}_{\text{HK}}(A)\le \text{s}(A) (\text{type}(A)+1)+2 \cdot \text{e}(A)\left (\frac{1}{2}-\text{s}(A) \right ).\end{align*}
In particular,
$\text{s}(A) \le {1}/{2}$
.
Proof. For every
$e \ge 1$
, we can write
\begin{align*}F^{e}_{*}A=A^{\oplus a_e} \oplus \omega_A^{\oplus b_e} \oplus M_e,\end{align*}
where
$a_e$
,
$b_e$
are non-negative integers and
$M_e$
is a maximal Cohen–Macaulay A-module that does not contain A and
$\omega_A$
as direct summands. Then
\begin{align*}F_{*}^e\omega_A \cong \text{Hom}_A\!\left(F^e_{*}A, \omega_A\right) \cong A^{\oplus b_e} \oplus \omega_A^{\oplus a_e} \oplus \text{Hom}_A\!\left(M_e,\omega_A\right).\end{align*}
By the argument in the proof of Sannai [ Reference Sannai35 , proposition 3·10], we have
\begin{align*}\lim_{e \to \infty} \frac{a_e}{\operatorname{rank} F_*^e A} = \lim_{e \to \infty} \frac{b_e}{\operatorname{rank} F_*^e A} = \text{s}(A).\end{align*}
Since
$M_e$
is a maximal Cohen–Macaulay A-module, we then have
\begin{align}\mu_A\!\left(F^{e}_{*}A\right) & = a_e + b_e \cdot \text{type}(A) + \mu_A(M_e)\nonumber\\& \le a_e + b_e \cdot \text{type}(A) +\text{e}_A(M_e) \nonumber\\ &= a_e + b_e \cdot \text{type}(A) +\text{e}(A) \operatorname{rank}_A (M_e) \nonumber\\ &= a_e + b_e \cdot \text{type}(A) +\text{e}(A) \!\left(\operatorname{rank} F_*^e A-a_e-b_e\right). \end{align}
Hence
\begin{align*}\dfrac{\mu_A(F^{e}_{*}A)}{\operatorname{rank} F^{e}_{*}A}\le\dfrac{a_e}{\operatorname{rank} F^{e}_{*}A} + \text{type}(A)\cdot \dfrac{b_e}{\operatorname{rank} F^{e}_{*}A}+ \text{e}(A) \!\left(1 - \dfrac{a_e}{\operatorname{rank} F^{e}_{*}A}- \dfrac{b_e}{\operatorname{rank} F^{e}_{*}A} \right),\end{align*}
and the first assertion follows after taking limits as e tends to
$\infty$
.
In particular, since
\begin{align*}0 \le \dfrac{\operatorname{rank}_A(M_e)}{\operatorname{rank} F^{e}_{*}A}= 1 - \dfrac{a_e}{\operatorname{rank} F^{e}_{*}A} - \dfrac{b_e}{\operatorname{rank} F^{e}_{*}A},\end{align*}
we get
$0 \le 1 - 2 \cdot \text{s}(A)$
, that is,
$\text{s}(A) \le {1}/{2}$
.
Remark 4·2. We note that there are examples of Gorenstein rings having F-signature at least
$\frac{1}{2}$
. The first example is a 2-dimensional Gorenstein strongly F-regular local ring: A is necessarily a hypersurface and has minimal multiplicity, thus
$\text{e}(A)=2$
. Therefore, we have
$\text{s}(A)=2-\text{e}_{\text{HK}}(A)\ge 2- {3}/{2} = {1}/{2}$
by [
Reference Watanabe and Yoshida48
, corollary 2·6] (see also [
Reference Watanabe and Yoshida46
, example 4·1] and [
Reference Huneke and Leuschke22
, example 18]). Second, the Segre product
$k[x,y] \# k[a,b]$
has F-signature
$2/3$
by Proposition 5·8.
The following theorem characterizes the equality in Proposition 4·1.
Theorem 4·3. Let A be a strongly F-regular local domain which is not Gorenstein. The following conditions are equivalent:
-
(i)
$\text{e}_{\text{HK}}(A) = \text{s}(A) (\text{type}(A)+1)+2 \cdot \text{e}(A) \left (\frac{1}{2}-\text{s}(A) \right )$
; -
(ii) each
$F^{e}_{*}A$
is a finite direct sum of A,
$\omega_A$
and an Ulrich A-module
$M_e$
.
Proof. For every
$e \ge 1$
, we can write
$F^{e}_{*}A=A^{\oplus a_e} \oplus \omega_A^{\oplus b_e} \oplus M_e$
, where
$a_e$
and
$b_e$
are non-negative integers and
$M_e$
is a maximal Cohen–Macaulay A-module that does not contain A and
$\omega_A$
as direct summands.
(ii)
$ \Longrightarrow$
(i): by the assumption,
$M_e$
is an Ulrich A-module, that is,
$\mu_A(M_e)=\text{e}(M_e)$
. Hence the assertion follows from the proof of Proposition 4·1.
(i)
$\Longrightarrow$
(ii): suppose that there exists e
′ such that
$F_{*}^{e^{\prime}}A=A^{\oplus a_{e^{\prime}}} \oplus \omega_A^{\oplus b_{e^{\prime}}} \oplus M_{e^{\prime}}$
, where
$M_{e^{\prime}}$
is an maximal Cohen–Macaulay A-module but not an Ulrich A-module, namely,
$\mu_A\!\left(M_{e^{\prime}}\right)< \text{e}\!\left(M_{e^{\prime}}\right)$
. By [
Reference Polstra and Smirnov31
, lemma 3·3] we may now build a similar decomposition for all
$e \geq e^{\prime}$
:
\begin{align*}F_*^e A = A^{\oplus a_{e}} \oplus \omega_A^{\oplus b_{e}} \oplus M_{e^{\prime}}^{\oplus c_e} \oplus N_e\end{align*}
such that
$\liminf_{e \to \infty} c_e/\operatorname{rank} F_*^e A > 0$
. Following the proof of Proposition 4·1 we obtain that
\begin{align*}\mu_A\!\left(F^{e}_{*}A\right) \leq a_e + b_e \cdot \text{type}(A) - c_e\!\left(\text{e}(M_e) - \mu_A(M_e)\right) + \text{e}(A) (\operatorname{rank} F_*^e A-a_e-b_e),\end{align*}
which shows after dividing by
$\operatorname{rank} F_*^e A$
and passing to the limit that
\begin{align*}\text{e}_{\text{HK}}(A) < \text{s}(A) (\text{type}(A)+1)+\text{e}(A) (1-2 \cdot \text{s}(A)).\end{align*}
One can prove the following proposition by a similar method as in the proof of Proposition 4·1 and Theorem 4·3.
Proposition 4·4. Suppose that A is an F-finite Gorenstein local ring of dimension
$d \ge 2$
. Then
\begin{align*}\text{e}_{\text{HK}}(A) \le \text{s}(A) + (1-\text{s}(A))\cdot \text{e}(A)\end{align*}
and the equality holds if and only if for all
$e\geq 1$
$F_{*}^eA$
can be written as a direct sum of A and Ulrich A-modules.
We note that if
$\text{e}(A)=2$
we have
$\text{e}_{\text{HK}}(A)=2-\text{s}(A)$
, and hence A satisfies the equality of Proposition 4·4.
Question 4·5. If A is Gorenstein and satisfies
$\text{e}_{\text{HK}}(A) = \text{s}(A) + (1-\text{s}(A))\cdot \text{e}(A)$
, then is
$\text{e}(A) \le 2$
?
We proceed to study non-Gorenstein rings whose F-signature is
${1}/{2}$
.
Theorem 4·6. Let A be an F-finite Cohen–Macaulay local domain which is not Gorenstein. Then the following conditions are equivalent
$:$
-
(i)
$\text{s}(A) = {1}/{2}$
, -
(ii) A is FFRT with the FFRT system
$\{A, \omega_A\}$
.
When this is the case,
$\text{e}_{\text{HK}}(A) = ({\text{type}(A)+1})/{2}$
.
Proof. (ii)
$\Longrightarrow $
(i) essentially follows from the proof of Proposition 4·1, because in this case there is no
$M_e$
and we have equality throughout.
(i)
$\Longrightarrow $
(ii): assume that for some
$e^{\prime} \ge 1$
, we write
$F^e_{*}A$
as
\begin{align*}F^{e^{\prime}}_{*}A=A^{\oplus a_{e^{\prime}}} \oplus \omega_A^{\oplus b_{e^{\prime}}} \oplus M_{e^{\prime}},\end{align*}
where
$0 \neq M_{e^{\prime}}$
is a maximal Cohen-Macaulay A-module that does not have A and
$\omega_A$
as direct summands. Since R is strongly F-regular by the assumption, as explained in [
Reference Polstra and Smirnov31
, lemma 3·3] we may now build similar decompositions for
$e \geq e^{\prime}$
:
\begin{align*}F_*^e A = A^{\oplus a_{e}} \oplus \omega_A^{\oplus b_{e}} \oplus M_{e^{\prime}}^{\oplus c_e} \oplus N_e\end{align*}
with
$\liminf_{e \to \infty} c_e/\operatorname{rank} F_*^e A > 0$
. After taking ranks we then have that
\begin{align*}1 \ge \dfrac{a_e}{\operatorname{rank} F_*^e A} + \dfrac{b_e}{\operatorname{rank} F_*^e A} + \operatorname{rank}_A M_{e^{\prime}}\dfrac{c_e}{\operatorname{rank} F_*^e A}\end{align*}
which after taking limits then gives that
$1 > \text{s} (A)+ \text{s}(A)$
which is a contradiction.
Let us give an example of local rings having
$\text{s}(A) = {1}/{2}$
.
Example 4·7. Let
$d \ge 2$
be an integer. Let
$A=k[[x_1,\ldots, x_d]]^{(2)}$
be the second Veronese subring of the formal power series ring over k. Then
$\text{s}(A) = {1}/{2}$
. Moreover, A is not Gorenstein if and only if d is odd.
Let A be a Cohen–Macaulay local domain with minimal multiplicity. Then A is not Gorenstein if and only if
$\text{e}(A) \ge 3$
. Moreover, then
$\text{type}(A)=\text{e}(A)-1$
. So we can obtain the following corollary by combining 3·6, 4·1, 4·6 and 4·3.
Corollary 4·8. Suppose that A is a Cohen–Macaulay local domain with minimal multiplicity and with
$\text{e}(A) \ge 3$
. Then:
-
(i)
$\text{s}(A) \le {1}/{2}$
; -
(ii)
${\text{e}(A)}/{2} \le \text{e}_{\text{HK}}(A) \le (1-\text{s}(A))\text{e}(A)$
; -
(iii) the following conditions are equivalent
$:$
-
(a)
$\text{s}(A) = \frac{1}{2}$
; -
(b) A has FFRT with the FFRT system
$\{A, \omega_A\}$
.When this is the case,
$\text{e}_{\text{HK}}(A) = {\text{e}(A)}/{2}$
.
-
-
(iv) Suppose
$\text{s}(A)>0$
. Then the following conditions are equivalent
$:$
-
(a)
$\text{e}_{\text{HK}}(A)=(1-\text{s}(A))\text{e}(A)$
; -
(b)
$F_{*}^eA$
can be written as a direct sum of A,
$\omega_A$
and Ulrich A-modules for every
$e \ge 1$
.
-
Example 4·9. Let
$A=k[[x,y,z]]^{(2)}$
. Then A has minimal multiplicity and its multiplicity is 4. Moreover,
$\text{e}_{\text{HK}}(A)= {\text{e}(A)}/{2}=2$
and
$\text{s}(A)= {1}/{2}$
.
Example 4·10. Let
$A=k[[x^3,xy^2,xy^2,y^3]]=k[[x,y]]^{(3)}$
. Then,
$F_{*}^eA$
can be written as direct sum of A,
$\omega_A=Ax+Ay$
and
$M=Ax^2+Axy+Ay^2$
. In this case,
$\text{s}(A)= {1}/{3}$
by [
Reference Watanabe and Yoshida47
], and
$\text{e}(A)=3$
,
$\text{type}(A)=2$
. Since
$\mu_A(M)=3=\text{e}_A(M)=\text{e}(A)\operatorname{rank}_A(M)$
, we see that M is an Ulrich A-module, and we have
\begin{align*}\text{e}_{\text{HK}}(A)=2=\text{s}(A) (\text{type}(A)+1)+2 \cdot \text{e}(A) \left (\frac{1}{2}-\text{s}(A)\right).\end{align*}
We pose the following question.
Question 4·11. Let A be a d-dimensional Cohen–Macaulay local domain with isolated singularity and that
$\text{s}(A)= {1}/{2}$
. Then is A isomorphic to the ring defined in Example 4·7?
4.1.
$\mathbb{Q}$
-Gorenstein local rings
We are able to give an affirmative answer to Question 4·11 in a particular case.
Let A be a Cohen-Macaulay reduced local ring. For an ideal
$I \subset A$
of pure height 1, the
$n^{\text{th}}$
symbolic power
$I^{(n)}$
denotes the intersection of height one primary components of
$I^n$
.
Definition 4·12. Let A be a normal local domain having a canonical module
$\omega_A$
.
-
(i) The ring A is said to be
$\mathbb{Q}$
-Gorenstein if there exists an ideal J of pure height 1 which is isomorphic to
$\omega_A$
as an A-module such that
$J^{(n)}$
is principal. Furthermore, is called the index of A. Note that A is Gorenstein if and only if it is
\begin{align*}\text{index}(A) \,:\!=\,\text{min}\left\{n \ge 1 \mid \text{$J^{(n)}$ is principal}\right\}\end{align*}
$\mathbb{Q}$
-Gorenstein of index 1.
-
(ii) Suppose that A is a
$\mathbb{Q}$
-Gorenstein normal local domain of
$r=\text{index}(A) \ge 2$
, and let J be an ideal such that
$J \cong \omega_A$
. Then the canonical cover of A is defined as
\begin{align*}B\,:\!=\, \bigoplus_{i=0}^{r-1} J^{(i)}.\end{align*}
We will use the following result due to Carvajal–Rojas [ Reference Carvajal–Rojas9 , theorem C] which extends prior work [ Reference Von Korff42 , theorem 2·6·5] and [ Reference Watanabe44 ].
Theorem 4·13. Let A be a strongly F-regular
$\mathbb{Q}$
-Gorenstein local domain and let
$r \ge 2$
be the index of A. Let B be the canonical cover of A. Then we have
$\text{s}(A)= \text{s}(B)/{r}$
.
Using this, we can prove the following theorem.
Theorem 4·14. Let A be an F-finite
$\mathbb{Q}$
-Gorenstein normal local domain of characteristic
$p>0$
. Assume the index r of A is at least 2. Then the following conditions are equivalent
$:$
-
(i)
$\text{s}(A)= {1}/{2}$
. -
(ii)
$r=2$
and A admits a canonical cover B which is regular.
Proof. Suppose (i). Let B a canonical cover of A. Then
$\text{s}(A)= {\text{s}(B)}/{r}$
. If
$r \ge 3$
, then
$\text{s}(B)=r\cdot \text{s}(A)> 1$
. This is a contradiction. Hence
$r =2$
and
$\text{s}(B)=1$
. Hence B is regular. The converse is easy.
4.2. The F-signatures of
$3$
-dimensional Gorenstein rings
We want to present a few upper bounds on F-signature in view of Question 1·1. We first estimate F-signature using the multiplicity.
Theorem 4·15. Let
$(A,\mathfrak{m},k)$
be a
$3$
-dimensional Gorenstein strongly F-regular local ring with multiplicity
${\text{e}(A) \ge 3}$
. Then
$\text{s}(A) \le {\text{e}(A)}/{24}$
.
Proof. Let J be a minimal reduction of
$\mathfrak{m}$
. Then we can write
$J \,:\, \mathfrak{m}=(J,u)$
for some
$u \in \mathfrak{m} \setminus J$
because A is Gorenstein. Moreover, we have
\begin{align*}\text{s}(A) \le \text{e}_{\text{HK}}(J)-\text{e}_{\text{HK}}(J\,:\, \mathfrak{m})=\text{e}(J)-\text{e}_{\text{HK}}(J \,:\, \mathfrak{m})=\text{e}(A)-\text{e}_{\text{HK}}(J\,:\, \mathfrak{m}).\end{align*}
Since A is strongly F-regular, applying the Briançon–Skoda theorem to
$J^{[q]}$
we get that
$\mathfrak{m}^{3q} \subset J^{[q]}$
, and thus
$\mathfrak{m}^2 \subset J \,:\, \mathfrak{m}$
. Since A is not double point,
$\mathfrak{m}^2 \not \subset J$
. Hence there exists an element
$v \in \mathfrak{m}^2$
such that
$v \in J \,:\, \mathfrak{m} \setminus J$
. Write
$v=a+ru$
for some
$a \in J$
and
$r \in A$
. Suppose
$r \in \mathfrak{m}$
. Then
$ru \in J$
and thus
$v=a+ru \in J$
, which is a contradiction. Hence
$r \in A \setminus \mathfrak{m}$
and
$(J,u)=(J,v)$
. So we may assume that
$u \in \mathfrak{m}^2$
. Then
$u^q \in \mathfrak{m}^{2q}$
and we get
\begin{align*}\ell_A \!\left(\dfrac{u^qA+J^{[q]}}{J^{[q]}}\right) &\le \ell_A\!\left(\dfrac{u^qA+\mathfrak{m}^{\lfloor\frac{5}{2}q\rfloor }+J^{[q]}}{J^{[q]}}\right) \\&\le \ell_A \!\left(\dfrac{u^qA+\mathfrak{m}^{\lfloor\frac{5}{2}q\rfloor }+J^{[q]}}{\mathfrak{m}^{\lfloor\frac{5}{2}q\rfloor }+J^{[q]}}\right) + \ell_A \!\left(\dfrac{\mathfrak{m}^{\lfloor\frac{5}{2}q\rfloor }+J^{[q]}}{J^{[q]}}\right).\end{align*}
Note that
$\overline{A}=A/J^{[q]}$
is an Artinian Gorenstein local ring. Thus the Matlis duality yields that
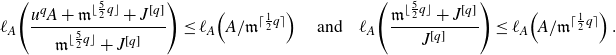\begin{align*}\ell_A \!\left(\dfrac{u^qA+\mathfrak{m}^{\lfloor\frac{5}{2}q\rfloor }+J^{[q]}}{\mathfrak{m}^{\lfloor\frac{5}{2}q\rfloor }+J^{[q]}}\right) \le \ell_A\!\left(A/\mathfrak{m}^{\lceil\frac{1}{2}q\rceil }\right)\quad \text{and} \quad\ell_A \!\left(\dfrac{\mathfrak{m}^{\lfloor\frac{5}{2}q\rfloor }+J^{[q]}}{J^{[q]}}\right)\le \ell_A\!\left(A/\mathfrak{m}^{\lceil\frac{1}{2}q\rceil }\right).\end{align*}
Therefore
\begin{align*}\text{s}(A) \le \lim_{e \to \infty} \ell_A \!\left(\dfrac{u^qA+J^{[q]}}{J^{[q]}}\right)/q^3\le 2 \cdot \lim_{e \to \infty}\dfrac{\ell_A\!\left(A/\mathfrak{m}^{\lceil \frac{1}{2}q\rceil }\right)}{q^3} =2 \times \dfrac{1}{3!} \left(\dfrac{1}{2}\right)^3\text{e}(A) =\dfrac{1}{24}\text{e}(A),\end{align*}
as required.
The next example shows that Theorem 4·15 gives the best possible bound.
Example 4·16. Let
$R^{(2)}$
be the
$2^{nd}$
Veronese subring of
$R=k[x,y,z,w]/(xw-yz)$
. Set
\begin{align*}A=k\left[\left[(x,y,z,w)^2\right]\right]/(xw-yz),\end{align*}
which is the completion with respect to the irrelevant maximal ideal
$\mathfrak{m}$
of
$R^{(2)}$
. Then A is a
$3$
-dimensional Gorenstein strongly F-regular local domain. Hence [
Reference Huneke and Watanabe23
, theorem 5·1(1)] implies
$\text{e}(A) \le \text{emb}(A)-1=8$
. On the other hand, since A is not hypersurface (of multiplicity 2),
$\text{e}(A) \ge \text{emb}(A)-\dim A+2 = 9-3+2=8$
and thus
$\text{e}(A)=8$
. Moreover, we have
\begin{align*}\text{s}(A)= \dfrac{\text{s}(R)}{2} = \dfrac{2/3}{2}=\dfrac{1}{3}=\dfrac{\text{e}(A)}{24}.\end{align*}
On the other hand, by [ Reference Watanabe and Yoshida46 , corollary 1·10], we have
\begin{align*}\text{e}_{\text{HK}}\!\left(\mathfrak{m}_R^2\right) =\, & \text{e}(\mathfrak{m})\left(\begin{array}{c}2 +3-2\\[4pt]3\end{array}\right) + \text{e}_{\text{HK}}(\mathfrak{m})\left(\begin{array}{c}2 +3-2\\[4pt]3-1\end{array}\right)\\& =\text{e}(R)+3 \cdot \text{e}_{\text{HK}}(R)=2+3 \cdot \frac{4}{3}=6.\end{align*}
Hence
\begin{align*}\text{e}_{\text{HK}}(A)=\dfrac{\text{e}_{\text{HK}}\!\left(\mathfrak{m}_A R\right)}{2}=\dfrac{\text{e}_{\text{HK}}(\mathfrak{m}_R^2)}{2}=\dfrac{6}{2}=3> \frac{7}{3}=\frac{8}{6}+1=\frac{\text{e}(A)}{6}+1.\end{align*}
Remark 4·17. The argument given in the proof of Theorem 4·15 is also valid for some classes of higher dimensional Gorenstein rings. A specific example is a hypersurface
$A\,:\!=\, k\left[\left[x_0,x_1,\ldots,x_d\right]\right]/\left(x_0^d+x_1^d+\cdots+x_d^d\right)$
. For the maximal ideal
$\mathfrak{m}$
and its minimal reduction J, we have that
$\mathfrak{m}^d\subset J$
and
$\mathfrak{m}^{d-1}\not\subset J$
. Thus, by the same argument as the proof of Theorem 4·15, we see that
$\text{s}(A)\le {\text{e}(A)}/{2^{d-1}d!} = {1}/{2^{d-1}(d-1)!}$
, see also [
Reference Watanabe and Yoshida47
, proposition 2·4 and question 2·6].
As the first open case, we will investigate Question 1·1, Conjecture 2·10 for 3-dimensional Gorenstein rings. In particular, we ask the following question.
Question 4·18. Let
$(A,\mathfrak{m})$
be a 3-dimensional non-regular Cohen-Macaulay local ring. Is
$\text{s}(A) \le {2}/{3}$
?
If this is correct, then this bound is best possible because if
$A = k[x,y,z,w]/(xw - yz )$
, then
${\text{s}(A)= {2}/{3}}$
. We will give a positive answer to this question for the case of toric rings in the next section (see Theorem 5·12). For a general situation, we only have the inequality given in Proposition 4·19.
Proposition 4·19. Let A be a
$3$
-dimensional strongly F-regular local domain which is not regular. Then
$\text{s}(A) < {5}/{6}$
.
Proof. We may assume that A is Gorenstein (see Proposition 4·1). By Proposition 4·4(1), we have
\begin{align*}\text{e}_{\text{HK}}(A) \le \text{s}(A)+\text{e}(A)(1-\text{s}(A)).\end{align*}
On the other hand, Theorem 3·7 implies that
\begin{align*}\frac{\text{e}(A)}{6}+1 \le \text{e}_{\text{HK}}(A) \le \text{s}(A)+\text{e}(A)(1-\text{s}(A)).\end{align*}
Hence
\begin{align*}\text{e}(A) \!\left(\text{s}(A) - \frac{5}{6}\right) \le \text{s}(A)-1 < 0.\end{align*}
and thus
$\text{s}(A) < {5}/{6}$
.
5. Observations on toric rings
In this section, we further study an upper bound on F-signature of a toric ring. In particular, in Theorem 5·12 we give a positive answer to Question 4·18.
5.1. Preliminaries
Let
$\textsf{N} \cong \mathbb{Z}^d$
be a lattice of rank d. Let
$\textsf{M}=\text{Hom}_{\mathbb{Z}}(\textsf{N},\mathbb{Z})$
be the dual lattice of
$\textsf{N}$
. We set
$\textsf{N}_{{\mathbb{R}}}=\textsf{N} \otimes_\mathbb{Z} {\mathbb{R}}$
and
$\textsf{M}_{{\mathbb{R}}} = \textsf{M} \otimes_\mathbb{Z} {\mathbb{R}}$
. We denote the inner product by
$\langle \quad, \quad \rangle \,:\,\textsf{M}_{\mathbb{R}} \times \textsf{N}_{\mathbb{R}} \to {\mathbb{R}}$
. Let
\begin{align*}\sigma \,:\!=\, {\mathbb{R}}_{\ge 0} v_1 + \cdots + {\mathbb{R}}_{\ge 0} v_n \subset \textsf{N}_{{\mathbb{R}}}\end{align*}
be a strongly convex rational polyhedral cone of dimension d generated by
$v_1,\ldots,v_n \in \mathbb{Z}^d$
where
$d \le n$
. We assume that
$v_1,\ldots,v_n$
are minimal generators of
$\sigma$
. Namely, the cone generated by any proper subset of
$\{v_1,\ldots,v_n\}$
is a proper subset of
$\sigma$
, and each
$v_i$
is the lattice point of smallest magnitude on the ray it generates. For each generator, we define the linear form
$\lambda_i ({-}) \,:\!=\, \langle - ,v_i\rangle$
. We consider the dual cone
$\sigma^{\vee}:$
\begin{align*}\sigma^{\vee} \,:\!=\, \left\{{\textbf{x}} \in \textsf{M}_{{\mathbb{R}}} \mid \lambda_i({\textbf{x}}) \ge 0 \;\text{ for all }\, i=1,2,\ldots,n\right\}.\end{align*}
In this case,
$\sigma^{\vee} \cap \textsf{M}$
is a positive normal affine monoid. Given an algebraically closed field k of characteristic
$p>0$
, we define the toric ring
\begin{align*}A\,:\!=\, k\left[\sigma^{\vee} \cap \textsf{M}\right] = k\left[t_1^{m_1}\cdots t_d^{m_d} \big| (m_1,\ldots,m_d) \in \sigma^{\vee} \cap \textsf{M}\right].\end{align*}
Thus, in this paper, a toric ring is a pointed normal affine monomial ring. In particular, any toric ring that we consider is strongly F-regular. We denote the irrelevant ideal of A as
${\mathfrak{m}}$
.
For each
${\textbf{a}}=(a_1,\ldots,a_n) \in \mathbb{Z}^n$
, we set
\begin{align*}V({\textbf{a}})\,:\!=\,\left\{{\textbf{x}} \in \textsf{M} \mid (\lambda_1({\textbf{x}}),\ldots, \lambda_n({\textbf{x}})) \ge\left(a_1,\ldots,a_n\right)\right\}.\end{align*}
Then we define the divisorial ideal (rank one reflexive module)
$D({\textbf{a}})$
generated by all monomials whose exponent vectors are in
$V({\textbf{a}})$
. For example, we have that
$R=D({\textbf{0}})$
and
$\omega_A \cong D(1,1,\ldots,1)$
. Let
$\mathfrak{p}_i\,:\!=\,D\!\left(\delta_{i1},\ldots,\delta_{in}\right)$
, where
$\delta_{ij}$
is the Kronecker delta. The height one prime ideals
$\mathfrak{p}_1,\ldots,\mathfrak{p}_n$
generate the class group
$\text{Cl}(A)$
. When we consider a divisorial ideal
$D({\textbf{a}})$
as the element of
$\text{Cl}(A)$
, we denote it by
$[D({\textbf{a}})]$
.
In what follows, we will pay attention to a certain class of divisorial ideals called conic.
Definition 5·1. (see e.g.[
Reference Bruns6, Reference Bruns and Gubeladze7
]). We say that a divisorial ideal
$D({\textbf{a}})$
is conic if there exist
${\textbf{x}} \in \textsf{M}_{{\mathbb{R}}}$
such that
${\textbf{a}}=\left(\ulcorner \lambda_1({\textbf{x}}) \urcorner, \ldots,\ulcorner \lambda_n({\textbf{x}}) \urcorner\right)$
, where
$\ulcorner \quad \urcorner$
stands for the round up.
Any conic divisorial ideal is a rank one maximal Cohen–Macaulay module (see [
Reference Bruns and Gubeladze7
, corollary 3·3]). We denote the set of isomorphism classes of conic divisorial ideals of a toric ring A by
$\mathcal{C}(A)$
. This is a finite set because the number of isomorphism classes of rank one maximal Cohen-Macaulay A-modules is finite (see [
Reference Bruns and Gubeladze7
, corollary 5·2]). The following proposition guarantees that any conic divisorial ideal appears in
$F_{*}^eA$
as a direct summand.
Theorem 5·2 ([
Reference Bruns and Gubeladze7
, proposition 3·6], [
Reference Smith and Van den Bergh37
, subsection 3·2]). Let A be a toric ring as above. Then, A has FFRT by the FFRT system
$\mathcal{C}(A)$
.
We recall that our arguments can be reduced to the
${\mathfrak{m}}$
-adic completion of A, as we mentioned in the beginning of Section 4. Thus, we may assume that A is complete local, in which case the Krull–Schmidt condition holds for A.
Remark 5·3. In some parts of this section, we assume that if the class group
$\text{Cl}(A)$
contains a torsion element, then the order of that element is coprime to p. In this case, the toric ring A is a ring of invariants.
Namely, let
$k^{\times}$
be the multiplicative group of k and
$G\,:\!=\,\text{Hom}(\text{Cl}(A),k^{\times})$
be the character group of
$\text{Cl}(A)$
. The group G acts on
$B\,:\!=\, k[x_1,\ldots,x_n]$
by
$g \cdot x_i=g([\mathfrak{p}_i])x_i$
for each
$g \in G$
and any i. Then, by [
Reference Bruns and Gubeladze7
, theorem 2·1(b)], A can be described as
$A \cong B^{G}$
. Moreover, to avoid the triviality, we assume that
$g([\mathfrak{p}_i])\neq1$
for any i, that is,
$[\mathfrak{p}_i]\neq0$
in
$\text{Cl}(A)$
.
Last, we will use that the F-signature of a toric ring can be computed combinatorially and, in particular, does not depend on the characteristic.
Theorem 5·4 ([ Reference Watanabe and Yoshida47 , theorem 5·1], see also [ Reference Bruns6 , Reference Singh36 , Reference Von Korff42 ]). Let A be a toric ring. Then, we may compute
\begin{align*}\text{s}(A)=\text{vol}\left\{\textbf{x}\in\textsf{M}_{\mathbb{R}} \mid 0\le \lambda_i(\textbf{x})\le 1 \,\, \text{for all} {i}\right\}.\end{align*}
5.2. Cohen–Macaulay toric rings
We recall that the F-signature of non-Gorenstein ring is less than or equal to
${1}/{2}$
(see Proposition 4·1). We now determine the non-Gorenstein toric rings whose F-signature is
${1}/{2}$
.
Proposition 5·5. Let A be a toric ring as in Remark 5·3. Then, the following conditions are equivalent.
-
(i) The FFRT system of A is
$\{A, M\}$
with
$M \not \cong A$
. -
(ii) A is isomorphic to the Veronese subring
$k[x_1,\ldots,x_d]^{(2)}$
of degree
$2$
.
When this is the case, the F-signature is
$\text{s}(A)={1}/{2}$
.
Proof. We first assume that the FFRT system of A is
$\{A, M\}$
. We note that
$M \cong \omega_A$
if A is not Gorenstein. In fact,
$\omega_A$
certainly appears in
$F_{*}^eA$
as a direct summand for sufficiently large e, since A is strongly F-regular (cf. [
Reference Sannai35
, proof of proposition 3·10], [
Reference Higashitani and Nakajima18
, proposition 2·1]). By [
Reference Bruns and Gubeladze7
, remark 3·4], the divisorial ideals
$\mathfrak{p}_1,\ldots,\mathfrak{p}_n$
are conic. Since
$\mathcal{C}(A)=\{A,M\}$
, we have that
$\mathfrak{p}_1\cong \cdots \cong \mathfrak{p}_n \cong M$
. Thus we have that
$[\mathfrak{p}_1]=\cdots = [\mathfrak{p}_n]=[M]$
in
$\text{Cl}(A)$
. On the other hand, since
$[\omega_A]=[\mathfrak{p}_1]+\cdots + [\mathfrak{p}_n]$
, we see that
$n[\mathfrak{p}_i]=0$
(resp.
$(n-1)[\mathfrak{p}_i]=0$
) in
$\text{Cl}(A)$
for any i if A is Gorenstein (resp. not Gorenstein). Thus we conclude that
$\text{Cl}(A)$
is a finite cyclic group generated by
$[\mathfrak{p}_i]$
, that is,
$\text{Cl}(A) \cong \langle [\mathfrak{p}_i] \rangle$
. By [
Reference Bruns and Gubeladze8
, corollary 4·59], this implies that the cone
$\sigma$
defining A is simplicial (i.e.,
$n=d$
), thus we have that
$A \cong B^{G}$
where
$B=k[x_1,\ldots,x_d]$
and
$G=\text{Hom}(\text{Cl}(A),k^{\times})$
is a finite cyclic group. We may assume that G is small (see e.g. [
Reference Iyama and Wemyss24
, proof of theorem 5·7]). By [
Reference Smith and Van den Bergh37
, proposition 3·2], each indecomposable direct summand of
$F_{*}^eA$
is a module of covariants which takes the form
$(B \otimes_k V_i)^G$
, where
$V_i$
is an irreducible representation of G. Since the FFRT system is
$\{A,M\}$
and G is small, we have only two non-isomorphic irreducible representations of G. Then we have that
$|G|=2$
, and the elements of G are the characters of
$\rho_0,\rho_1\in \text{Hom}(\text{Cl}(A),k^{\times})$
defined by
$\rho([\mathfrak{p}_i])=1$
and
$\rho([\mathfrak{p}_i])=-1$
respectively. Consequently, we have that
$A \cong k[x_1,\ldots,x_d]^{(2)}$
. By [
Reference Watanabe and Yoshida47
, theorem 4·2], the F-signature of
$A\cong B^G$
is
${1}/{|G|}= {1}/{2}$
.
On the other hand, we assume that
$A\cong k[x_1,\ldots,x_d]^{(2)}$
. Then, A is the invariant subring of
$k[x_1,\ldots,x_d]$
under the action of the cyclic group
$\langle g=\text{ diag}({-}1,\ldots,-1)\rangle$
defined by
$g\cdot x_i=-x_i$
for any i. Thus, the condition (i) follows from [
Reference Smith and Van den Bergh37
, proposition 3·2·1].
This is the main result in this subsection.
Theorem 5·6. Let A be a toric ring as Remark 5·3. Assume that A is not Gorenstein, then the following conditions are equivalent.
-
(i)
$\text{s}(A)= {1}/{2}$
. -
(ii) The FFRT system of A is
$\{A,\omega_A\}$
. -
(iii) A is isomorphic to the Veronese subring
$k[x_1,\ldots,x_d]^{(2)}$
of degree
$2$
, where d is an odd number.
Proof. (iii)
$ \Longrightarrow $
(i) follows from [
Reference Watanabe and Yoshida47
, theorem 4·2]. (i)
$ \Longleftrightarrow $
(ii) follows from Theorem 4·6. Then we show (ii)
$ \Longleftrightarrow $
(iii). By Proposition 5·5, we see that
$A \cong k[x_1,\ldots,x_d]^{(2)} = k[x_1,\ldots,x_d]^{G}$
, where
$G \cong \langle \text{diag}({-}1,\ldots,-1)\rangle$
. Since A is not Gorenstein, G is not a subgroup of SL(d,k), thus d is an odd number (see [
Reference Watanabe43
]).
Example 5·7. If A is a Gorenstein toric ring, then
$\text{s}(A)= {1}/{2}$
does not imply the conditions (ii) and (iii) in Theorem 5·6. Namely, consider the Segre product
$P_n\,:\!=\, k[x_1,y_1]\#\cdots\# k[x_n,y_n]$
of n polynomial rings with two variables, which is a Gorenstein toric ring in dimension
$n+1$
. Then, by [
Reference Higashitani and Nakajima18
, proposition 6·1], one can compute
$\text{s}(P_n)= {2}/({n+1})$
. For example,
$\text{s}(P_3)= {1}/{2}$
but the FFRT system of
$P_3$
consists of 7 conic divisorial ideals (see [
Reference Higashitani and Nakajima17
, example 2·6]).
This example shows that it is difficult to bound F-signature of a Gorenstein ring A using the number of modules in the FFRT system. For this reason, we give an observation regarding Gorenstein toric rings whose the FFRT system consists of three modules.
Proposition 5·8. Let A be a toric ring as in Remark 5·3. We assume that A is Gorenstein. Then, the following conditions are equivalent.
-
(i) The FFRT system of A is
$\{A, M_1, M_2\}$
, -
(ii) A is isomorphic to one of the following rings:
-
(a) the invariant subring
$k[x_1,\ldots,x_d]^G$
where
$G=\left\langle\text{\rm diag}\!\left(\underbrace{\xi,\ldots,\xi}_{m},\underbrace{\xi^2,\ldots,\xi^2}_{m}\right)\right\rangle$
with
$d=2m$
and
$\xi$
is a primitive cubic root of unity, in which case
$\text{s}(A)= {1}/{3}$
, -
(b) the Segre product
$k[x_1,y_1]\# k[x_2,y_2]=k[x_1x_2,x_1y_2,y_1x_2,y_1y_2]$
of two polynomial rings, in which case
$\text{s}(A)= {2}/{3}$
.
-
Proof. We first show (i)
$\Longrightarrow$
(ii). By [
Reference Higashitani and Nakajima18
, proposition 2·1], we have that
$M_1\cong M_2^*$
. Since
$\mathfrak{p}_i$
is conic, each
$\mathfrak{p}_i$
is isomorphic to either
$M_1$
or
$M_1^*$
. Moreover, since
$[\omega_A]=[\mathfrak{p}_1]+\cdots+[\mathfrak{p}_n]=0$
, we see that n is an even number and we may assume that
\begin{align*}[\mathfrak{p}_1]=\cdots=[\mathfrak{p}_m]=-[\mathfrak{p}_{m+1}]=\cdots=-[\mathfrak{p}_n]\end{align*}
where
$n=2m$
. Then, we see that
$\text{Cl}(A)$
is generated by
$[\mathfrak{p}_1]$
, and we have two cases depending on whether it is torsion.
-
(i) If
$\text{Cl}(A)\cong \mathbb{Z}/r\mathbb{Z}$
, then, by an argument similar to the proof of Proposition 5·5,
$G\cong \mathbb{Z}/3\mathbb{Z}$
. For a generator g of G, we can set
$g([\mathfrak{p}_1])=\xi$
where
$\xi$
is a primitive cubic root of unity. In this case, the action of G in S can be described as and we have the case (a). The F-signature of A can be obtained from [ Reference Watanabe and Yoshida47 , theorem 4·2].
\begin{align*}\begin{cases}g\cdot x_i=\xi x_i&(i=1,\ldots,m),\\g\cdot x_i=\xi^{-1}x_i=\xi^2 x_i&(i=m+1,\ldots,n),\end{cases}\end{align*}
-
(ii) If
$\text{Cl}(A)\cong \mathbb{Z}$
, then we see that
$G\cong k^\times$
and if
$g([\mathfrak{p}_1])=\zeta\in k^\times$
for a generator g of G, then
$g({-}[\mathfrak{p}_1])=\zeta^{-1}$
. Thus, the action of G on B can be described as In this case, we have that
\begin{align*}\begin{cases}g\cdot x_i=\zeta x_i&(i=1,\ldots,m),\\g\cdot x_i=\zeta^{-1}x_i&(i=m+1,\ldots,n).\end{cases}\end{align*}
This Segre product of two polynomial rings can be considered as a Hibi ring [ Reference Hibi16 ], and the conic classes in Hibi rings are characterized in [ Reference Higashitani and Nakajima17 ]. By [ Reference Higashitani and Nakajima17 , theorem 2·4 and example 2·6], we see that the Segre products of two polynomial rings that satisfy the condition (i) are only the one with
\begin{align*}A\cong k[x_1,\ldots,x_m]\#k[x_{m+1},\ldots,x_n]=k[x_ix_j\mid i=1,\ldots,m,\, j=m+1,\ldots,n].\end{align*}
$m=2$
. Thus, we have that
$\text{s}(A) = {2}/{3}$
by Example 5·7 (the case of
$n=2$
), or we easily see that
$A\cong k[x,y,z,w]/(xw - yz )$
, in which case
$\text{s}(A) = \text{e}(A) - \text{e}_{\text{HK}}(A) = 2 - {4}/{3} = {2}/{3}$
.
(ii)
$\Longrightarrow$
(i) is well known, see e.g. [
Reference Smith and Van den Bergh37
, proposition 3·2] for the case (a) and [
Reference Toda and Yasuda39
, the proof of theorem 6·1] for (b).
5.3. Maximal toric F-signatures
In this subsection, we completely classify the toric rings A for which
$s(A) > {1}/{2}$
. To this purpose, it will be helpful to introduce the following notation.
Definition 5·9. For
$w_1,\dots,w_m\in \textsf{N}$
, a finite set of vectors in the lattice
$\textsf{N}$
, define the dual zonotope as
\begin{align*} {\mathcal{P}^{\vee} \!\left(\{ {w_1,\dots,w_m} \}\right) } = \left\{\textbf{x} \in \textsf{M}_{{\mathbb{R}}} \;|\; \langle \textbf{x} , w_i \rangle \in [0,1]\right\}\,. \end{align*}
In this notation, Theorem 5·4 says that
$s(k[\sigma^{\vee} \cap \textsf{M}]) = \textrm{vol}\ {\mathcal{P}^{\vee} (\{ {v_1,\dots,v_n} \}) }$
, where
$v_1,\dots,v_n$
are the minimal generators of
$\sigma$
.
Our techniques will be based on volumes of slices of the unit cube, as in Section 3. First, we interpret certain volumes as Eulerian numbers.
Lemma 5·10. The volume of the portion of the unit d-cube where the sum of the coordinates lies between k and
$k+1$
is
$ {A(d,k)}/{d!}$
, where A(d, k) denotes the Eulerian number with parameters d and k.
Proof. The following argument is due to Stanley [
Reference Stanley38
]. The hyperplanes
$x_i=x_j$
cut the interior of the unit cube into
$d!$
simplices of equal volume. Each can be characterized as the set of points
$\Delta_{\sigma}$
where
$0<x_{\sigma(1)}<x_{\sigma(2)}<\dots<x_{\sigma(d)}<1$
for some
$\sigma\in\mathcal{S}_d$
, giving a natural bijection between the simplices and
$\mathcal{S}_d$
. Define a map
\begin{align*}\phi(x_1,\dots,x_d)_i=\begin{cases}x_{i+1}-x_i & \textrm{ if } x_i<x_{i+1}\textrm{ and }i\not=d \\1+x_{i+1}-x_i & \textrm{ if } x_i>x_{i+1}\textrm{ and }i\not=d \\1-x_n & \textrm{ if }i=d \,. \\\end{cases}\end{align*}
Note that
$\phi$
maps into the unit cube, and that
$\phi|_{\Delta_{\sigma}}$
is affine with determinant
$\pm1$
. Further, if
$(x_1,\dots,x_d)\in{\Delta_{\sigma}}$
, then
\begin{align*}k\leq \phi(x_1,\dots,x_d)_1+\dots+\phi(x_1,\dots,x_d)_d\leq k+1\,,\end{align*}
where k is the number of descents of
$\sigma$
. Additionally, the map
\begin{align*}\psi(x_1,\dots,x_d)_i=\lceil{x_i+\dots +x_n}\rceil-({x_i+\dots +x_n})\end{align*}
provides an inverse for
$\phi$
on its image.
Lemma 5·11. For the Eulerian numbers A(d, k),
${A(d,k)}/{d!} > {1}/{2}$
if and only if
$(d,k)=(1,0)$
,
$(3,1)$
or
$(5,2)$
.
Proof. By symmetry, it is clear that
$ {A(d,k)}/{d!} < {1}/{2}$
for an even integer d. Let
$k\geq 3$
; we will show that
$ {A(2k+1,k+j)}/{(2k+1)!} < \frac{1}{2}$
by induction. The values can explicitly checked for
$k=3$
. By twice applying the relation
\begin{align*}A(n,m)=(n-m)\ A(n-1,m-1)+(m+1)\ A(n-1,m)\end{align*}
one obtains the equality
\begin{align*}A(2k+1,k+j)=\,&(k-j+1)!\ A(2k-1,k-j-2)+(k+j+1)!\ A(2k-1,k-j)\\ &+2(k^2+k-j^2)\ A(2k-1,k-j-1)\,.\end{align*}
By induction, this is less than
$(2k-1)!\ \left(k^2+\frac{3}{2} k+ \frac{1}{2}\right),$
which, for
$k\geq 3$
, is less than
$\frac{1}{2}(2k+1)!$
as required.
Theorem 5·12. The toric rings with F-signature greater than
$1/2$
are, up to isomorphism, as follows:
-
(i) for a polynomial ring A, we have
$s(A)=1$
; -
(ii) for the coordinate ring A of the Segre product
$\mathbb{P}^1 \# \mathbb{P}^1$
, we have
$s(A)= {2}/{3}$
; -
(iii) for the coordinate ring A of the Segre product
$\mathbb{P}^2 \# \mathbb{P}^2$
, we have
$s(A) = {11}/{20}$
.
Proof. We use the notation of Subsection 5·1. We can write
\begin{equation} {\mathcal{P}^{\vee} \!\left(\left\{ {v_1,\dots,v_n} \right\}\right) } = \bigcap_{\left\{j_1, \ldots, j_d\right\}\subset \{1,\dots,n\}} {\mathcal{P}^{\vee} \!\left(\left\{ {v_{j_1},\dots,v_{j_d}} \right\}\right) } \,.\end{equation}
By the Jacobian formula,
\begin{align*} \operatorname{vol}\!\left({\mathcal{P}^{\vee} \!\left(\left\{ {v_{j_1},\dots,v_{j_d}} \right\}\right) }\right) = \left|\frac{1}{\det{\left[v_{j_1},\dots,v_{j_d}\right]}}\right| \,.\end{align*}
Thus, if
$s(R)> {1}/{2}$
,
$\big|\det{\left[v_{j_1},\dots,v_{j_d}\right]}\big|=1$
for any
$\left\{j_1, \ldots, j_d\right\}\subset \left\{1,\dots,n\right\}$
. Assume for now that this is the case. If
$n=d$
, then
$\{v_1,\dots,v_n\}$
is a basis for
$\textsf{M}$
, so A is isomorphic to a polynomial ring.
Consider the case where
$n=d+1$
. The vectors
$\{v_1,\dots,v_d\}$
form a basis for
$\textsf{N}$
. Let
$x_1,\dots,x_d$
be coordinates of
$\textsf{M}$
forming a dual basis to
$v_1,\dots,v_d$
. We may thus compute the volume of
$ {\mathcal{P}^{\vee} \!\left(\left\{ {v_1,\dots,v_n} \right\}\right) }$
in these coordinates. Since
$|\det{[v_1,\dots,\widehat{v_i},\dots,v_d,v_{d+1}]}|=1$
, the
$i^{th}$
coordinate of
$v_{d+1}$
is
$\pm 1$
. That is, in these coordinates,
\begin{align*} [v_1,\dots,v_{d+1}]=\left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}1 & 0 & ... & 0 & \pm 1 \\[2pt]0 & 1 & ... & 0 & \pm 1 \\[2pt]\vdots & \vdots & \ddots & \vdots & \vdots \\[2pt]0 & 0 & ... & 1 & \pm 1 \\[2pt]\end{array}\right]\,.\end{align*}
Note that if
$d\leq 2$
, then our generating set for
$\sigma$
is not minimal, so we may assume that
$d\geq 3$
. Renumber the coordinates so that in the matrix above,
$\langle x_i, v_{d+1}\rangle=+1$
for
$i\leq k$
and
$\langle x_i, v_{d+1}\rangle=-1$
for
$i>k$
. Then
${\mathcal{P}^{\vee} (\{ {v_1,\dots,v_{d+1}} \}) }$
is the subset of the unit d-cube where
\begin{align*}0\leq x_1+\cdots+x_k-x_{k+1}-\cdots-x_d\leq 1\,.\end{align*}
Using
$x_j\mapsto 1-x_j$
symmetry of the cube, we have
\begin{align*} \operatorname{vol}\!\left({\mathcal{P}^{\vee} \!\left(\left\{ {v_1,\dots,v_{d+1}} \right\}\right) }\right) = \operatorname{vol}\!\left(\left\{\left(x_1,\dots,x_d\right)\in[0,1]^d \;|\; k\leq \sum_{i=1}^d x_i \leq k+1 \,\right\}\right) \,.\end{align*}
By Lemma 5·11, we see that the volume s(A) is greater than
${1}/{2}$
only if
$d=3$
and
$k=1$
or
$d=5$
and
$k=2$
. These correspond to the coordinate rings of
$\mathbb{P}^1 \# \mathbb{P}^1$
and
$\mathbb{P}^2 \# \mathbb{P}^2$
.
We now consider what happens if
$n\geq d+2$
. If
$\operatorname{vol}({\mathcal{P}^{\vee} (\{ {v_1,\dots,v_n} \}) })>1/2$
, with
$d=3$
, then
\begin{align*} [v_1,\dots,v_4]=\left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c}1 & 0 & 0 & 1 \\[2pt]0 & 1 & 0 & 1 \\[2pt]0 & 0 & 1 & -1 \\\end{array}\right]\end{align*}
in the dual basis to
$v_1, v_2, v_3$
. If
$n\geq 5$
, the same arguments show that if
$\operatorname{vol}({\mathcal{P}^{\vee} (\{ {v_1,\dots,v_n} \}) })> {1}/{2}$
, in a particular basis we have
\begin{align*} [v_1,\dots,v_5]=\left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}1 & 0 & 0 & 1 & 1\\[2pt]0 & 1 & 0 & 1 & -1\\[2pt]0 & 0 & 1 & -1 & 1\\\end{array}\right],\end{align*}
where one computes
$\operatorname{vol}({\mathcal{P}^{\vee} (\{ {v_1,\dots,v_5} \}) })=1/3$
. Thus, the F-signature cannot be greater than or equal to
$1/2$
in this case. Now consider
$d=5$
. If
$\operatorname{vol}({\mathcal{P}^{\vee} (\{ {v_1,\dots,v_n} \}) })> {1}/{2}$
,
\begin{align*} [v_1,\dots,v_6]=\left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}1 & 0 & 0 & 0 & 0 & 1 \\[3pt]0 & 1 & 0 & 0 & 0 & 1 \\[3pt]0 & 0 & 1 & 0 & 0 & 1 \\[3pt]0 & 0 & 0 & 1 & 0 & -1 \\[3pt]0 & 0 & 0 & 0 & 1 & -1 \\\end{array}\right] \end{align*}
in the dual basis to
$v_1, v_2, v_3, v_4, v_5$
. If
$n\geq 7$
, a case-by-case analysis similar to above shows that the volume
$\operatorname{vol}({\mathcal{P}^{\vee} (\{ {v_1,\dots,v_n} \}) })< {1}/{2}$
.
If A is not a toric ring, we have a family of 3-dimensional Gorenstein rings whose F-signature are greater than
${1}/{2}$
.
Example 5·13. Let
$c>2$
be an integer. Put
$A\,:\!=\,k[[x,y,z,w]]/\left(x^2+y^2+z^2+w^c\right)$
, where k is an algebraically closed field of characteristic
$p >c$
. Then, A is a normal hypersurface of
$\dim A=3$
, and
\begin{align*}\dfrac{1}{2} < \text{s}(A) < \dfrac{2}{3}.\end{align*}
In fact, since
$\text{e}(A)=2$
we have that
$\text{s}(A)=2-\text{e}_{\text{HK}}(A)$
, thus this follows from [
Reference Watanabe and Yoshida48
, corollary 3·11].
Acknowledgements
This work started during the third author’s stay at the Nihon University and he thanks them for hospitality. The second author would like to thank Kazuhiko Kurano, Akihiro Higashitani and Kohsuke Shibata for valuable discussions. The authors also want to thank the anonymous referee for the insightful comments that improved the quality and readability of our manuscript.
The first author is supported by by NSF CAREER Award DMS-2044833. The second author is supported by World Premier International Research Center Initiative (WPI initiative), MEXT, Japan, JSPS Grant-in-Aid for Young Scientists (B) 17K14159, and JSPS Grant-in-Aid for Early-Career Scientists 20K14279. At various times during the preparation of this manuscript, the third author had support of a Starting Grant 2020-03970 by the Swedish Research Council and of a fellowship from “la Caixa” Foundation (ID 100010434) and from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska–Curie grant agreement No 847648. The fellowship code is “LCF/BQ/PI21/11830033”. The fifth author was partially supported by JSPS Grant-in-Aid for Scientific Research (C) Grant Numbers 19K03430.
The content of subsection 5·3 originally appeared in the first author’s Ph.D. thesis [Reference Jeffries25].
Open access
