Hostname: page-component-848d4c4894-mwx4w Total loading time: 0 Render date: 2024-06-30T23:34:04.478Z Has data issue: false hasContentIssue false
  • English
  • Français

A Generalization of Picard's Method of Successive Approximation

Published online by Cambridge University Press:  24 October 2008

H. O. Hirschfeld
H. O. Hirschfeld
Affiliation:
Fitzwilliam House
Get access Rights & Permissions [Opens in a new window]

Extract

It is well known that the boundary value problem for the non-linear differential equation

can be reduced with help of a Green's function K (x, ξ) to a non-linear integral equation of the type

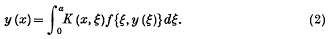
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 32 , Issue 1 , January 1936 , pp. 86 - 95
Copyright
Copyright © Cambridge Philosophical Society 1936

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Picard, E., Journ. de Math. (4), 9 (1893), 217.Google Scholar

† Hammerstein, A., Acta Math. 54 (1930), 118–22.CrossRefGoogle Scholar

† A similar argument in another connection was used by Signorini, Palermo Rend. 33 (1912), 187–93; Birkhoff, , Trans. Amer. Math. Soc. 18 (1912), 199–300CrossRefGoogle Scholar; and especially Morse, M., Trans. Amer. Math. Soc. 27 (1925), 213–34.Google Scholar

‡ See (a) Bogoliouboff, N. and Kryloff, N., Annals of Math. (2), 29 (1928), 255–75CrossRefGoogle Scholar, and (b) Kryloff, N., Tôhoku Math. Journ. 28 (1927), 65–8.Google Scholar In the latter paper our problem is treated under the condition 0 ≤ f ν (x, y) ≤ A with the help of Ritz' method; the error estimation is reduced to that of some other trigonometrical approximation of the solution.

§ We can replace this hypothesis by assuming only that f ν (x, y) is bounded, if, instead of differentiating with regard to a, in (iv), we use a geometrical argument due to R. Brauer (see Bieberbach, , Differentialgleichungen, Berlin, 3 Aufl. p. 197).Google Scholar

* Compare E. Picard, loc. cit.

† These functions were called y r (x; a r, a r−1) in (iii). The change of notation will be justified at once.

‡ If (A′) is true, we could choose for I the value of and for n any integer greater than since the solution then has the minimizing property.

* Compare M. Morse, loc. cit. p. 228.

* Where n is chosen according to footnote ‡ on p. 90.

† It will be obvious by (19) and (7), that this set is stationary for large N and it could be made stationary for any N by a proper choice of I.

* Loc. cit. p. 271

† Loc. cit. p. 258.