Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-27T00:35:14.641Z Has data issue: false hasContentIssue false
  • English
  • Français

Curvature, causality and completeness in space-times with causally complete spacelike slices

Published online by Cambridge University Press:  24 October 2008

Gregory J. Galloway
Gregory J. Galloway
Affiliation:
Department of Mathematics, University of Miami, Coral Gables, FL 33124, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

Let S be a spacelike slice (defined formally in Section 2) in a space-time M. We will say that S is future causally complete in M if for each p ε J+(S) the closure in S of the set J-(p) ∩ S is compact. Define past causal completeness time-dually. Then S is causally complete if it is both future and past causally complete. A compact spacelike slice is necessarily causally complete, as is any Cauchy surface, but the concept of causal completeness is much broader than either of these two conditions. For example the slices t = const. ≠ 0 in the space-time obtained by removing the origin from Minkowski space are causally complete, although they are neither Cauchy nor compact. The slice t = 0 in the previous example and the hyperboloid 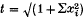in Minkowski space (where (t, x1, …, xn) are standard inertial coordinates) are examples of slices which are not causally complete. Physically speaking, an edgeless slice S is future causally complete if the information from S which reaches a point in the future of S comes from a finite nonsingular region in S. The Maximal Reissner-Nordstrom space-time is a well-known example in which this finiteness condition is not fulfilled by any of its asymptotically flat partial Cauchy surfaces. Indeed for any such partial Cauchy surface S, J-(p) ∩ S is non-compact for any p ε H+(S). However, as has been discussed in the literature (e.g. [17], p. 625 f), it is believed that the Cauchy horizon in this situation is unstable with respect to perturbations of the initial data on S.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 99 , Issue 2 , March 1986 , pp. 367 - 375
Copyright
Copyright © Cambridge Philosophical Society 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bartnik, R.. Existence of maximal hypersurfaces in asymptotically flat space-times. Commun. Math. Phys. 94 (1984), 155–175.CrossRefGoogle Scholar
[2]Beem, J. K. and Ehrlich, P. E.. Global Lorentzian Geometry. Pure and Applied Mathematics, vol. 67 (Marcel Dekker, 1981).Google Scholar
[3]Beem, J. K., Ehrlich, P. E., Markvorsen, S. and Galloway, G. J.. Decomposition theorems for Lorentzian manifolds with nonpositive curvature. J. Diff. Geom., to appear.Google Scholar
[4]Borde, A.. A note on compact Cauchy horizons. Phys. Lett. A 102 (1984), 224–226.CrossRefGoogle Scholar
[5]Borde, A.. Singularities in closed space-time. Classical Quantum Gravity, to appear.Google Scholar
[6]Clarke, C. J. S. and De Felice, F.. Globally noncausal space-times II. Naked singularities and curvature conditions. Gen. Relativity Gravitation J. 16 (1984), 139–148.CrossRefGoogle Scholar
[7]Galloway, G. J.. Splitting theorems for spatially closed space-times. Commun. Math. Phys. 96 (1984), 423–429.CrossRefGoogle Scholar
[8]Geroch, R. P.. Topology in general relativity. J. Math. Phys. 8 (1967), 782–786.CrossRefGoogle Scholar
[9]Harris, S. G.. On maximal geodesic diameter and causality in Lorentzian manifolds. Math. Ann. 261 (1982), 307–313.CrossRefGoogle Scholar
[10]Hawking, S. W. and Ellis, G. F. R.. The Large Scale Structure of Space-time (Cambridge University Press, 1973).CrossRefGoogle Scholar
[11]Krolak, A.. Strong curvature singularities, trapped surfaces, and the cosmic censorship hypothesis. (Preprint.)Google Scholar
[12]Lindblom, L. and Brill, D. R.. Comments on the topology of nonsingular stellar models. In Essays in General Relativity, ed. Tipler, F. J. (Academic Press, New York, 1980).Google Scholar
[13]Newman, R. P. A. C.. Cosmic censorship and curvature growth. Gen. Relativity Gravitation J. 15 (1983), 641–653.CrossRefGoogle Scholar
[14]O'Neill, B.. Semi-Riemannian Geometry (Academic Press, 1983).Google Scholar
[15]Penrose, R., Techniques of Differential Topology in Relativity, Regional Conference Series in Applied Mathematics, vol. 7, SIAM (Philadelphia, 1972).CrossRefGoogle Scholar
[16]Penrose, R.. Singularities of space time. In Theoretical Principles in Astrophysics and Relativity, eds Lebovitz, N. R., Reid, W. H. and Vandervoort, P. O. (University of Chicago Press, 1978).Google Scholar
[17]Penrose, R.. Singularities and time-asymmetry. In General Relativity. An Einstein Centenary Survey, eds. Hawking, S. W. and Israel, W. (Cambridge University Press, 1979).Google Scholar
[18]Tipler, F. J.. Causality violation in asymptotically flat space-times. Phys. Rev. Lett. 37 (1976), 879–882.CrossRefGoogle Scholar