Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-26T15:47:09.725Z Has data issue: false hasContentIssue false
  • English
  • Français

A convex 3-complex not simplicially isomorphic to a strictly convex complex

Published online by Cambridge University Press:  24 October 2008

Robert Connelly  and
David W. Henderson
Robert Connelly
Affiliation:
Cornell University, Ithaca
David W. Henderson
Affiliation:
Cornell University, Ithaca
Get access Rights & Permissions [Opens in a new window]

Extract

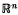A set X in euclidean space is convex if the line segment joining any two points of X is in X. If X is convex, every boundary point is on an (n − 1)-plane which contains X in one of its two closed half-spaces. Such a plane is called a support plane for X. A simplicial complex K in is called strictly convex if |K| (the underlying space of K) is convex and if, for every simplex σ in ∂K (the boundary of K) there is a support plane for |K| whose intersection with |K| is precisely σ In this case |K| is often called a simplicial polytope.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 88 , Issue 2 , September 1980 , pp. 299 - 306
Copyright
Copyright © Cambridge Philosophical Society 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Barnette, D. Diagrams and Schegel-diagrams in Combinatorial structures and their applications (New York, Gordon and Breach, 1970), pp. 1–4.Google Scholar
(2)Bing, R. H.An alternate proof that 3-manifolds can be triangulated, Ann. of Math. 69 (1959), 37–65.CrossRefGoogle Scholar
(3)Cairns, S. S.Triangulated manifolds which are not Brouwer manifolds. Ann. of Math. 41 (1940), 792–795.CrossRefGoogle Scholar
(4)Chillingworth, D. R.J. Collapsing three-dimensional convex polyhedra. Proc. Cambridge Philos. Soc. 63 (1967), 353–357.CrossRefGoogle Scholar
(5)Crapo, H. and Whiteley, W. Stressed frameworks and projected polytopes. Groupe de Recherche Topologie Structurale (Université de Montreal, 1978 preprint).Google Scholar
(6)Cremona, L.Graphical statics (Oxford University Press, 1872).Google Scholar
(7)Ewald, G. and Shephard, G. C.Stellar subdivisions of boundary complexes of convex polytopes. Math. Ann. 210 (1974), 7–16.CrossRefGoogle Scholar
(8)Goodrick, R. E.Non-simplicially collapsible triangulations of I n. Proc. Cambridge Philos. Soc. 64 (1968), 31–36.CrossRefGoogle Scholar
(9)Grünbaum, B.Convex Polytopes (New York, Wiley, 1967).Google Scholar
(10)Grünbaum, B. and Sreedharan, V. P.An enumeration of simplicial 4-polytopes with 8 vertices. J. Combinatorial Theory 2 (1967), 437–465.CrossRefGoogle Scholar
(11)Lickorish, W. B. R. and Martin, J. M.Triangulations of the 3-Ball with knotted spanning 1-simplices and collapsible r-th derived subdivisions. Trans. Amer. Math. Soc. 137 (1969), 451–458.Google Scholar
(12)Mani, P.Spheres with few vertices. J. Combinatorial Theory (A) 13 (1972), 346–352.CrossRefGoogle Scholar
(13)Maxwell, J. C.On reciprocal figures and diagrams of forces. Phil. Mag., series 4, 27 (1864), 250–261.CrossRefGoogle Scholar
(14)Rourke, C. P. and Sanderson, B. J.An introduction to piecewise-linear topology (Springer-Verlag, 1972).CrossRefGoogle Scholar
(15)Shephard, G. C.Spherical complexes and radial projections of polytopes. Israel J. Math. 9 (1971), 257–262.CrossRefGoogle Scholar
(16)Steinitz, E.Polyeder und Raumeinteilungen. Enzyhl. Math. Wiss. 3 (Geometrie), Part 3AB12 (1922), 1–139.Google Scholar
(17)Supnick, F.On the perspective deformation of polyhedra. Ann. of Math. 49 (1948), 714–730; 53 (1951), 551–555.CrossRefGoogle Scholar
(18)van Kampen, E. R. Remark on the address of S. S. Cairns, Lectures in Topology, University of Michigan Conference 1940, ed. Wilder, R. L. (Ann Arbor, Ayres, 1941), pp. 311–313.Google Scholar
(19)Whitehead, J. H. C.On subdivisions of complexes. Proc. Cambridge Philos. Soc. 31 (1935), 69–75.CrossRefGoogle Scholar
(20)Zeeman, E. C.Seminar on Combinatorial Topology (I.H.E.S., 1963).Google Scholar
(21)Bruggesser, H. and Mani, P.Shellable decompositions of cells and spheres. Math. Scand. 29 (1971), 197–205.CrossRefGoogle Scholar
(22)Rudin, M. E.An unshellable triangulation of a tetrahedron. Bull. Amer. Math. Soc. 64, no. 3 (1958), 90–91.CrossRefGoogle Scholar
(23)McMullen, P.The maximum numbers of faces of a convex polytope. Mathematika 17 (1970), 179–184.CrossRefGoogle Scholar
(24)Schutlt, C.An invertable 3-diagram with 8 vertices. Discrete math. 28 (1979), 201–205.Google Scholar