Hostname: page-component-848d4c4894-v5vhk Total loading time: 0 Render date: 2024-07-03T12:07:39.025Z Has data issue: false hasContentIssue false
  • English
  • Français

Completed tensor products and a global approach to p-adic analytic differential operators

Published online by Cambridge University Press:  20 June 2018

ANDREAS BODE
ANDREAS BODE*
Affiliation:
Mathematical Institute, Andrew Wiles Building, University of Oxford, Radcliffe Observatory Quarter, Woodstock Road, Oxford, OX2 6GG. e-mail: Andreas.Bode@maths.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Ardakov-Wadsley defined the sheaf 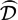$\wideparen{\Ncal{D}}$X of p-adic analytic differential operators on a smooth rigid analytic variety by restricting to the case where X is affinoid and the tangent sheaf admits a smooth Lie lattice. We generalise their results by dropping the assumption of a smooth Lie lattice throughout, which allows us to describe the sections of 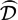$\wideparen{\Ncal{D}}$ for arbitrary affinoid subdomains and not just on a suitable base of the topology. The structural results concerning 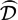$\wideparen{\Ncal{D}}$ and coadmissible 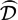$\wideparen{\Ncal{D}}$-modules can then be generalised in a natural way.

The main ingredient for our proofs is a study of completed tensor products over normed K-algebras, for K a discretely valued field of mixed characteristic. Given a normed right module U over a normed K-algebra A, we provide several exactness criteria for the functor 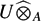$U\widehat{\otimes}_A$ - applied to complexes of strict morphisms, including a necessary and sufficient condition in the case of short exact sequences.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 167 , Issue 2 , September 2019 , pp. 389 - 416
Copyright
Copyright © Cambridge Philosophical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Ardakov, K. Equivariant $\Ncal{D}$-modules on rigid analytic spaces, arXiv 1708.07475v1 [math.RT] (2017).Google Scholar
[2] Ardakov, K. and Johansson, C. A canonical dimension estimate for non-split semisimple p-adic Lie groups. Represent. Theory 20 (2016), 128–138.Google Scholar
[3] Ardakov, K. and Wadsley, S. J. $\wideparen{\Ncal{D}}$-modules on rigid analytic spaces I. arXiv 1501.02215 [math.NT], (2015).Google Scholar
[4] Berthelot, P. $\mathscr{D}$-modules arithmétiques I. Operateurs differentiels de niveau fini. Ann. Sci. Éc. Norm. Sup. (4), 29 (1996), no. 2, 185–272.Google Scholar
[5] Bode, A. A proper mapping theorem for coadmissible $\wideparen{\Ncal{D}}$-modules. In preparation.Google Scholar
[6] Bosch, S. Lectures on formal and rigid geometry. Lecture Notes in Math. vol. 2105 (Springer-Verlag, 2014).Google Scholar
[7] Bosch, S., Güntzer, U. and Remmert, R.. Non-Archimedean Analysis (Springer-Verlag, 1984).Google Scholar
[8] Bourbaki, N. Algèbre: chaiptres 1-3 (Hermann, 1970).Google Scholar
[9] Bourbaki, N. Commutative algebra: chapters 1–7 (Springer-Verlag, 1989).Google Scholar
[10] Emerton, M. Locally analytic vectors in representations of locally p-adic groups. Mem. Amer. Math. Soc. 248 (2017), no. 1175.Google Scholar
[11] Grothendieck, A. and Dieudonné, J. Elements de geometrie algebrique III. Publ. Math. IHES 11, 1961.Google Scholar
[12] Nastasescu, C. and van Oystaeyen, F. Graded Ring Theory (North Holland, 1982).Google Scholar
[13] Rinehart, G. S. Differential forms on general commutative algebras. Trans. Amer. Math. Soc. 108 (1963), 195–222.Google Scholar
[14] Schmidt, T. Stable flatness of nonarchimedean hyperenveloping algebras. J. Algebra 323 (2010), no. 3, 757–765.Google Scholar
[15] Schmidt, T. Verma modules over p-adic Arens–Michael envelopes of reductive Lie algebras. J. Algebra 390 (2013), 160–180.Google Scholar
[16] Schneider, P. Nonarchimedean Functional Analysis (Springer-Verlag, 2002).Google Scholar
[17] Schneider, P. and Teitelbaum, J. Algebras of p-adic distributions and admissible representations. Invent. Math., 153 (2003), no. 1, 145–196.Google Scholar
[18] The Stacks Project Authors. Stacks Project. http://stacks.columbia.edu (2017).Google Scholar
[19] Weibel, C. A. An introduction to homological algebra Camb. Stud. Adv. Math. vol. 38 (Cambridge University Press, 1994).Google Scholar