Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-28T12:18:39.140Z Has data issue: false hasContentIssue false
  • English
  • Français

The BNSR-invariants of the Lodha–Moore groups, and an exotic simple group of type 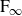$\textrm{F}_\infty$

Part of: Special aspects of infinite or finite groups Low-dimensional topology

Published online by Cambridge University Press:  04 April 2022

YASH LODHA  and
MATTHEW C. B. ZAREMSKY
YASH LODHA
Affiliation:
Department of Mathematics, Universität Wien, Oskar-Morgenstern-Platz 1, 1090 Wien, Austria. e-mail: yashlodha763@gmail.com
MATTHEW C. B. ZAREMSKY
Affiliation:
Department of Mathematics and Statistics, University at Albany (SUNY), 1400 Washington Ave, Albany, NY 12222, U.S.A. e-mail: mzaremsky@albany.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we give a complete description of the Bieri–Neumann–Strebel–Renz invariants of the Lodha–Moore groups. The second author previously computed the first two invariants, and here we show that all the higher invariants coincide with the second one, which finishes the complete computation. As a consequence, we present a complete picture of the finiteness properties of normal subgroups of the first Lodha–Moore group. In particular, we show that every finitely presented normal subgroup of the group is of type 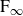$\textrm{F}_\infty$ , answering a question posed in Oberwolfach in 2018. The proof involves applying a variation of Bestvina–Brady discrete Morse theory to the so called cluster complex X introduced by the first author. As an application, we also demonstrate that a certain simple group S previously constructed by the first author is of type $\textrm{F}_\infty$ . 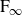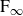This provides the first example of a type $\textrm{F}_\infty$ simple group that acts faithfully on the circle by homeomorphisms, but does not admit any nontrivial action by 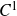$C^1$ -diffeomorphisms, nor by piecewise linear homeomorphisms, on any 1-manifold.

MSC classification

Primary: 20F65: Geometric group theory
Secondary: 57M07: Topological methods in group theory
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 174 , Issue 1 , January 2023 , pp. 25 - 48
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bestvina, M. Brady, N.. Morse theory and finiteness properties of groups. Invent. Math. 129.3 (1997), 445–470.CrossRefGoogle Scholar
Burillo, J., Cleary, S. Röver, C. E.. Obstructions for subgroups of Thompson’s group V. In Geometric and Cohomological Group Theory London Math. Soc. Lecture Note Ser., 1–4 vol. 444 (Cambridge University Press, Cambridge, 2018).CrossRefGoogle Scholar
Bieri, R. Geoghegan, R.. Connectivity properties of group actions on non-positively curved spaces. Mem. Amer. Math. Soc. 161. 765 (2003), xiv+83.CrossRefGoogle Scholar
Bieri, R. Geoghegan, R.. Sigma invariants of direct products of groups. Groups Geom. Dyn. 4.2 (2010), 251–261.CrossRefGoogle Scholar
Bieri, R., Geoghegan, R. Kochloukova, D. H.. The sigma invariants of Thompson’s group F. Groups Geom. Dyn. 4.2 (2010), 263–273.CrossRefGoogle Scholar
Belk, J., Hyde, J. Matucci, F.. Embeddings of $\mathbb{Q}$ into some finitely presented groups. arXiv:2005.02036.Google Scholar
Burillo, J., Lodha, Y. Reeves, L.. Commutators in groups of piecewise projective homeomorphisms. Adv. Math. 332 (2018), 34–56.CrossRefGoogle Scholar
Bonatti, C., Lodha, Y. and Triestino, M.. Hyperbolicity as an obstruction to smoothability for one-dimensional actions. Geom. Topol. 23.4 (2019), 1841–1876.Google Scholar
Bieri, R., Neumann, W. D. Strebel, R.. A geometric invariant of discrete groups. Invent. Math. 90.3 (1987), 451–477.CrossRefGoogle Scholar
Bieri, R. Renz, B.. Valuations on free resolutions and higher geometric invariants of groups. Comment. Math. Helv. 63.3 (1988), 464–497.CrossRefGoogle Scholar
Brown, K. S.. Finiteness properties of groups. In Proceedings of the Northwestern Conference on Cohomology of Groups (Evanston, Ill., 1985), vol. 44 (1987), 45–75.Google Scholar
Burillo, J.. Notes on the Lodha–Moore groups. https://web.mat.upc.edu/pep.burillo/book_en.php.Google Scholar
Bux, K.-U.. Finiteness properties of soluble arithmetic groups over global function fields. Geom. Topol. 8 (2004), 611–644.Google Scholar
Ghys, É. Sergiescu, V.. Sur un groupe remarquable de difféomorphismes du cercle. Comment. Math. Helv. 62.2 (1987), 185–239.CrossRefGoogle Scholar
Higman, G.. Finitely presented infinite simple groups. Department of Pure Mathematics, Department of Mathematics, I.A.S. (Australian National University, Canberra, 1974). Notes on Pure Mathematics, no. 8 (1974).Google Scholar
Lodha, Y. Moore, J. T.. A nonamenable finitely presented group of piecewise projective homeomorphisms. Groups Geom. Dyn. 10.1 (2016), 177–200.CrossRefGoogle Scholar
Lodha, Y.. A nonamenable type $\text{F}_\infty$ group of piecewise projective homeomorphisms. J. Topol. 13.4 (2020), 1767–1838.CrossRefGoogle Scholar
Lodha, Y.. A finitely presented infinite simple group of homeomorphisms of the circle. J. Lond. Math. Soc. (2) 100.3 (2019), 1034–1064.CrossRefGoogle Scholar
Cohomological and metric properties of groups of homeomorphisms of R. Oberwolfach Rep., 15.2 (2018), 1579–1633. Abstracts from the workshop held June 3–9, 2018. Organised by Burillo, J., Bux, K.-U. B. Nucinkis.CrossRefGoogle Scholar
Meier, J., Meinert, H. VanWyk, L.. Higher generation subgroup sets and the $\Sigma$ -invariants of graph groups. Comment. Math. Helv. 73.1 (1998), 22–44.CrossRefGoogle Scholar
Stein, M.. Groups of piecewise linear homeomorphisms. Trans. Amer. Math. Soc. 332.2 (1992), 477–514.CrossRefGoogle Scholar
Zaremsky, M. C. B.. Geometric structures related to the braided Thompson groups. Math. Z. To appear. arXiv:1803.02717.Google Scholar
Zaremsky, M. C. B.. HNN decompositions of the Lodha–Moore groups, and topological applications. J. Topol. Anal. 8.4 (2016), 627–653.CrossRefGoogle Scholar
Zaremsky, M. C. B.. Separation in the BNSR-invariants of the pure braid groups. Publ. Mat. 61.2 (2017), 337–362.CrossRefGoogle Scholar
Zaremsky, M. C. B.. On the $\Sigma$ 1invariants of generalised Thompson groups and Houghton groups. Int. Math. Res. Not. IMRN 2017.19 (2017), 5861–5896.Google Scholar