Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jiang, Yujiao
and
Lü, Guangshi
2020.
The Bombieri–Vinogradov Theorem on Higher Rank Groups and its Applications.
Canadian Journal of Mathematics,
Vol. 72,
Issue. 4,
p.
928.
Han, Xue
Yan, Xiaofei
and
Zhang, Deyu
2021.
On Fourier Coefficients of the Symmetric Square L-Function at Piatetski-Shapiro Prime Twins.
Mathematics,
Vol. 9,
Issue. 11,
p.
1254.
Ding, Wenjing
Liu, Huafeng
and
Zhang, Deyu
2021.
New Zero-Density Results for Automorphic L-Functions of GL(n).
Mathematics,
Vol. 9,
Issue. 17,
p.
2061.
Zhang, De Yu
and
Zhai, Wen Guang
2021.
On the Distribution of Hecke Eigenvalues over Piatetski-Shapiro Prime Twins.
Acta Mathematica Sinica, English Series,
Vol. 37,
Issue. 9,
p.
1453.
Huang, Jing
Liu, Huafeng
and
Wu, Jie
2021.
Divisor Problems Related to Hecke Eigenvalues in Three Dimensions.
Journal of Mathematics,
Vol. 2021,
Issue. ,
p.
1.
Huang, Jing
Liu, Huafeng
and
Zhang, Deyu
2021.
Power moments of automorphic L-functions related to Maass forms for SL
3(ℤ).
Open Mathematics,
Vol. 19,
Issue. 1,
p.
1007.
Zou, Aiyue
Lao, Huixue
Luo, Shu
and
Wu, Jie
2021.
Some Density Results on Sets of Primes for Hecke Eigenvalues.
Journal of Mathematics,
Vol. 2021,
Issue. ,
p.
1.
Huang, Jing
Liu, Huafeng
and
Xu, Fuxia
2021.
Two-Dimensional Divisor Problems Related to Symmetric L-Functions.
Symmetry,
Vol. 13,
Issue. 2,
p.
359.
Zhang, Rui
and
Yan, Xiaofei
2021.
The third-power moment of the Riesz mean error term of symmetric square $ L $-function.
AIMS Mathematics,
Vol. 6,
Issue. 9,
p.
9436.
Wang, Qian
and
Han, Xue
2022.
Comparing the number of ideals in quadratic number fields.
Mathematical Modelling and Control,
Vol. 2,
Issue. 4,
p.
268.
Huang, Jing
Li, Taiyu
Liu, Huafeng
and
Xu, Fuxia
2022.
The general two-dimensional divisor problems involving Hecke eigenvalues.
AIMS Mathematics,
Vol. 7,
Issue. 4,
p.
6396.
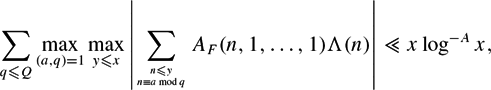 $$\sum_{q\leq Q}\max_{(a,q)=1}\max_{y\leq x}\left|\sum_{n\leq y \atop n\equiv a\bmod q}A_F(n,1, \dots, 1)\Lambda(n)\right| \ll x\log^{-A}x,$$
$$\sum_{q\leq Q}\max_{(a,q)=1}\max_{y\leq x}\left|\sum_{n\leq y \atop n\equiv a\bmod q}A_F(n,1, \dots, 1)\Lambda(n)\right| \ll x\log^{-A}x,$$



