Hostname: page-component-77c89778f8-sh8wx Total loading time: 0 Render date: 2024-07-19T03:13:41.278Z Has data issue: false hasContentIssue false
  • English
  • Français

Introduction to the theory of operators. IV Linear functionals

Published online by Cambridge University Press:  24 October 2008

S. W. P. Steen
S. W. P. Steen
Affiliation:
Christ's CollegeCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

This paper is a continuation of three others under the same title. The paragraphs are numbered following on to those of the third paper.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 35 , Issue 4 , November 1939 , pp. 562 - 578
Copyright
Copyright © Cambridge Philosophical Society 1939

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

† Steen, , Proc. London Math. Soc. (2), 41 (1936), 361–92CrossRefGoogle Scholar; 43 (1937), 529–43; 44 (1938), 398–411.

‡ This is required in § XXIII, Cor. (iv), etc.

† Annals of Math. 37 (1936), 116–229Google Scholar.

‡ Banach, , Opérations linéaires (1932), p. 53.Google Scholar

† Math. Ann. 102 (1929), 370–427.Google Scholar

‡ Hausdorff, , Mengenlehre, 2nd ed. (1927), p. 228.Google Scholar

§ Kantorovitch, , C.R. Acad. Sci. U.R.S.S. 14 (1937), 535.Google Scholar

† Take B*A, A*B for A, B respectively in the first part of the proof.

† If A is real and λ+(A) ≥ O for all λ+, then A ≥ O. For A = A + − A −, A + ≥ O, A − ≥ O, A +A − = O. λ+(A −A) is a positive linear functional equal to therefore A − = O.

‡ This is possible, since as n → ∞.

§ We have, by Cor. (x), If ∥ A ∥ = a, then A* A ≤ a 2I, whence Similarly [Cor. (x) with Thus | λ+(A) | ≤ 2aλ+(I), and so ‖λ+ ‖ ≤ 2λ+(I). By hypothesis, given k < 0, we can choose n and λ+ so that | λ+(A n) | > kλ+(I); hence we can choose n and λ+ so that | λ+(A 2)| > ½K‖ λ+‖. Clearly we can take ‖ λ+ ‖ to be any positive number (by multiplying λ+ by a suitable constant). Thus if we fix 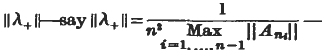then given k′ > 0 we can find n and λ+ so that | λ+(A n) | > k′. We need only take

† A′ belongs to the same association as the A n, since O = A n: A m → A′: A m(s) as n → ∞ (Cor. xvii), and O → O(s).

† For definitions of these terms see Ore, , Annals of Math. 36 (1935), 406–37.CrossRefGoogle Scholar

‡ Rank has only been defined for real operators. Left and right ranks are defined for any operators.

† This takes the place of lemma 7.3.1 in the paper “On rings of operators”, and Cor. (xiii) takes the place of lemma 6.2.2.

† We omit proofs that can be obtained directly from the paper “On rings of operators”. This is lemma 6. 1. 1. Cor. (iv) is lemma 6.2.3.

‡ V* × E = V* × E″ × E = V* × E″ = V*.

† 6·3 to Th. VIII.

‡ If E and F are projections, then (E vF) − F ≼ E. For (E vF) − F is the left rank of E − F × E. We have {(E vF) − F} × {E − F × E} = E − F × E. Hence (E vF) − F ≥ left rank of E − F × E. Let the left rank be (E vF) − F − G, where G is a projection and GF = O, G < E vF. Then G × (E − F × E) = O, i.e. G × E = O; hence G × (E vF) = O, thus G = O. Hence