Articles
Teaching the Shakespeare of Mathematics
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 385-397
-
- Article
- Export citation
R. L. Goodstein and the Mathematical Association
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 398-408
-
- Article
- Export citation
R. L. Goodstein and mathematical logic
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 409-412
-
- Article
- Export citation
Gauging the earth
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 413-420
-
- Article
- Export citation
Regular Polyhedral Clones
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 421-429
-
- Article
- Export citation
Γ2 (½)is more than just π
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 430-434
-
- Article
- Export citation
Derangement revisited
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 435-440
-
- Article
- Export citation
3D Generalisations of Viviani's theorem
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 441-445
-
- Article
- Export citation
An alternative approach to a problem by A. de Moivre
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 446-454
-
- Article
- Export citation
A simple series representation for Apéry's constant
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 455-460
-
- Article
- Export citation
Divisibility properties for Fibonacci and related numbers
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 461-464
-
- Article
- Export citation
Fun with Sign
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 465-473
-
- Article
- Export citation
Splitting a triangle
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 474-493
-
- Article
- Export citation
Notes
97.39 Fibonometry
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 494-495
-
- Article
- Export citation
97.40 Infinitely many proofs that there are infinitely many primes
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 495-498
-
- Article
- Export citation
97.41 The equation py 2 = x 4 + x
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 498-501
-
- Article
- Export citation
97.42 The Bombelli approach to solving cubic equations
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 501-504
-
- Article
- Export citation
97.43 Evaluation of
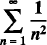 by a double integral
by a double integral
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 504-505
-
- Article
- Export citation
97.44 Another proof that ζ(2) = π2/6 via double integration
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 506-507
-
- Article
- Export citation
97.45 On Euler's Basel problem
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 508-510
-
- Article
- Export citation



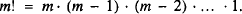
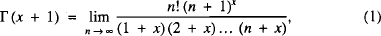
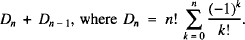
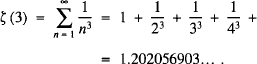
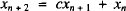
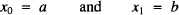
 and ½, and we would like to quantify the area of this region (as a fraction of the total area of the triangle) as
and ½, and we would like to quantify the area of this region (as a fraction of the total area of the triangle) as 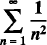 by a double integral
by a double integral