Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-26T09:48:26.053Z Has data issue: false hasContentIssue false
  • English
  • Français

The Laplace Transformation Method in Elementary Circuit Theory

Published online by Cambridge University Press:  03 November 2016

J. C. Jaeger
Get access Rights & Permissions [Opens in a new window]

Extract

1. Heaviside’s operational method has for some time been in fairly general use among engineers for solving problems in circuit theory, and appears in most of their textbooks. The average man who has read these seems able to manipulate the “expansion theorem” and to solve problems in which E.M.F is applied to an initially “dead” circuit, but he is not at all clear about the foundations or correctness of the theory and apt to be worried by any slightly more complicated problem, such as cases in which the circuit is not initially dead or problems involving switching operations (which are usually dealt with in the textbooks by artifice). It is now pretty well recognised that the Laplace transformation provides a satisfactory approach to the operational methods, but it is not perhaps fully realised just how simple it is and how extremely easy to teach.

Type
Research Article
Information
The Mathematical Gazette , Volume 24 , Issue 258 , February 1940 , pp. 42 - 50
Copyright
Copyright © Mathematical Association 1940

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page no 42 note * Math. Gazette, 22 (1938), 264.

page no 42 note † The method in precisely the form given here dates back at least to Bateman, Proc. Cambridge Phil. Soc., 15 (1910), 423.

page no 42 note ‡ Van der Pol, , Phil. Mag. (7) 7, (1923), 1153 CrossRefGoogle Scholar, and in many subsequent papers has used in place of (1)

and he has bee11 followed by many writers. The notation (1′) has the advantage that f(p) corresponds exactly to the Heavinide operator for the function h(t), whereas the of (1) would differ from it by a factor p. But the factor p of (1′) is simply carried as a passenger through the algebra and sometimes leads to increased complication, e.g. in replacing the simple idea of expansion in partial fractions by the use of the “Expansion Theorem”. Also the form (1) (though not the notation) is used by Doetsch in his standard work, Theorie und Anwendung der Laplace-Transformation (Berlin, 1931), and by write1.s on the mathematical theory.

page no 42 note § For example, if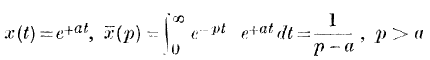

page no 43 note * The equation of order n and simultaneous equations are dealt with in the same way, cf. Carslaw, loc. cit.

page no 44 note * This follows immediately from Lerch’s Theorem, Doetsch, loc. cit., p. 35. A simple case of Lerch’s Theorem which is adequate for our purpose is that if for every p greater than some fixed number, and if x(t) is continuous, then x(t)≡0. If two continuous functions x 1(t) and x 2 (t) both have for Laplace transform we should have , and thus, by the result above, x 1(t)≡x 2(t).

page no 45 note * I owe this notation to Professor Bailey of Sydney university. It will be found very convenient in manuscript.

page no 45 note † I is taken positive when flowing towards the high-potential side of the condenser.

page no 46 note * This was given by Pipes [Phil. Mag. (7), 24 (1937), 502], but he obtains I(t) from Ī by contour integration; this is an unnecessary complication when only ordinary differential equations are being considered.