Hostname: page-component-848d4c4894-cjp7w Total loading time: 0 Render date: 2024-06-19T11:55:26.982Z Has data issue: false hasContentIssue false
  • English
  • Français

An Algebraic Theorem Related to the Theory of Relativity

Published online by Cambridge University Press:  03 November 2016

M. D. Dampier
M. D. Dampier*
Affiliation:
Department of Mathematics, Leicester University
Get access Rights & Permissions [Opens in a new window]

Extract

In a common development of the special theory of relativity one considers two events P and Q, P being the emission of a flash of light and Q the reception of the light. We suppose Q to be infinitesimally close to P and, by using the principle of the invariance of c, the velocity of light, argue that the infinitesimal coordinate differences between P and Q must satisfy

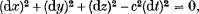Iand

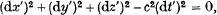II

where dx; etc. are the coordinate differences in one inertial frame whilst dx' etc. are those in a second inertial frame (e.g. [1], p. 16).

Type
Research Article
Information
The Mathematical Gazette , Volume 56 , Issue 398 , December 1972 , pp. 292 - 295
Copyright
Copyright © Mathematical Association 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Rindler, W.: Special Relativity. Oliver & Boyd (1960).Google Scholar
2. Pauli, W.: The Theory of Relativity. Pergamon (1958).Google Scholar
3. Moller, C.: The Theory of Relativity. Oxford (1952).Google Scholar
4. Marder, L.: An Introduction to Relativity. Longman (1968).Google Scholar