Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-26T10:14:24.576Z Has data issue: false hasContentIssue false
  • English
  • Français

Roots of sparse polynomials over a finite field

Part of: Finite fields and commutative rings (number-theoretic aspects)

Published online by Cambridge University Press:  26 August 2016

Zander Kelley
Zander Kelley*
Affiliation:
Texas A&M University, College Station,TX 77843, USA email zander_k@tamu.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a 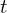$t$-nomial 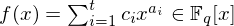$f(x)=\sum _{i=1}^{t}c_{i}x^{a_{i}}\in \mathbb{F}_{q}[x]$, we show that the number of distinct, nonzero roots of 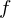$f$ is bounded above by 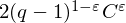$2(q-1)^{1-\unicode[STIX]{x1D700}}C^{\unicode[STIX]{x1D700}}$, where 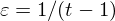$\unicode[STIX]{x1D700}=1/(t-1)$ and 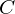$C$ is the size of the largest coset in 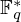$\mathbb{F}_{q}^{\ast }$ on which 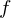$f$ vanishes completely. Additionally, we describe a number-theoretic parameter depending only on 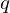$q$ and the exponents 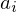$a_{i}$ which provides a general and easily computable upper bound for $C$. We thus obtain a strict improvement over an earlier bound of Canetti et al. which is related to the uniformity of the Diffie–Hellman distribution. Finally, we conjecture that 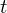$t$-nomials over prime fields have only 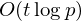$O(t\log p)$ roots in 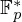$\mathbb{F}_{p}^{\ast }$ when 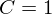$C=1$.

MSC classification

Primary: 11T06: Polynomials
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 196 - 204
Copyright
© The Author 2016 

References

Balog, A., Broughan, K. and Shparlinski, I. E., ‘On the number of solutions of exponential congruences’, Acta Arith. 148 (2010) no. 1, 93–103.CrossRefGoogle Scholar
Bi, J., Cheng, Q. and Rojas, J. M., ‘Sub-linear root detection, and new hardness results, for sparse polynomials over finite fields’, Proceedings of ISSAC (International Symposium on Symbolic and Algebraic Computation, June 26–29, Boston) (ACM Press, New York, 2013) 61–68.Google Scholar
Canetti, R., Friedlander, J. B., Konyagin, S., Larsen, M., Lieman, D. and Shparlinski, I. E., ‘On the statistical properties of Diffie–Hellman distributions’, Israel J. Math. 120 (2000) 23–46.CrossRefGoogle Scholar
Cheng, Q., Gao, S., Rojas, J. M. and Wan, D., ‘Sparse univariate polynomials with many roots over finite fields’, Preprint, 2014, arXiv:1411.6346.Google Scholar
Friedlander, J., Larsen, M., Lieman, D. and Shparlinski, I. E., ‘On the correlation of binary M-sequences’, Des. Codes Cryptogr. 16 (1999) no. 3, 249–256.CrossRefGoogle Scholar
Kelley, Z. and Owen, S., ‘Estimating the number of roots of trinomials over finite fields’, J. Symbolic Comput. (special issue on the topics of MEGA 2015), to appear; arXiv:1510.01758.Google Scholar
Shparlinski, I. E., ‘Sparse polynomial approximation in finite fields’, Proceedings of the Thirty-third Annual ACM Symposium on Theory of Computing (ACM Press, New York, 2001) 209–215.Google Scholar
Shparlinski, I. E., ‘On the singularity of generalised Vandermonde matrices over finite fields’, Finite Fields Appl. 11 (2005) no. 2, 193–199.Google Scholar