Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Vincent, Christelle
2018.
Advances in the Mathematical Sciences.
Vol. 15,
Issue. ,
p.
79.
Gélin, Alexandre
Howe, Everett
and
Ritzenthaler, Christophe
2019.
Principally polarized squares of elliptic curves
with field of moduli equal to ℚ.
The Open Book Series,
Vol. 2,
Issue. 1,
p.
257.
Ionica, Sorina
Kılıçer, Pınar
Lauter, Kristin
Lorenzo García, Elisa
Mânzăţeanu, Adelina
Massierer, Maike
and
Vincent, Christelle
2019.
Modular invariants for genus 3 hyperelliptic curves.
Research in Number Theory,
Vol. 5,
Issue. 1,
Kılıçer, Pınar
Lauter, Kristin
García, Elisa Lorenzo
Newton, Rachel
Ozman, Ekin
and
Streng, Marco
2020.
A bound on the primes of bad reduction for CM curves of genus 3.
Proceedings of the American Mathematical Society,
Vol. 148,
Issue. 7,
p.
2843.
Dina, Bogdan Adrian
and
Ionica, Sorina
2020.
Genus 3 hyperelliptic curves with CM via Shimura reciprocity.
Open Book Series,
Vol. 4,
Issue. 1,
p.
161.
Scholl, Travis
2020.
Super-isolated abelian varieties.
Journal of Number Theory,
Vol. 206,
Issue. ,
p.
138.
Kılıçer, Pınar
Lorenzo García, Elisa
and
Streng, Marco
2020.
Primes Dividing Invariants of CM Picard Curves.
Canadian Journal of Mathematics,
Vol. 72,
Issue. 2,
p.
480.
Lario, Joan-C.
Somoza, Anna
and
Vincent, Christelle
2021.
An inverse Jacobian algorithm for Picard curves.
Research in Number Theory,
Vol. 7,
Issue. 2,
Avanzi (ARM), Roberto
2021.
Encyclopedia of Cryptography, Security and Privacy.
p.
1.
Kirschmer, Markus
Narbonne, Fabien
Ritzenthaler, Christophe
and
Robert, Damien
2021.
Spanning the isogeny class of a power of an elliptic curve.
Mathematics of Computation,
Vol. 91,
Issue. 333,
p.
401.
Dina, Bogdan
Ionica, Sorina
and
Sijsling, Jeroen
2022.
Isogenous hyperelliptic and non-hyperelliptic Jacobians with maximal complex multiplication.
Mathematics of Computation,
Vol. 92,
Issue. 339,
p.
349.
LORENZO GARCÍA, Elisa
2022.
On different expressions for invariants of hyperelliptic curves of genus 3.
Journal of the Mathematical Society of Japan,
Vol. 74,
Issue. 2,
Avanzi, Roberto
and
Thériault, Nicolas
2022.
Encyclopedia of Cryptography, Security and Privacy.
p.
1.
Ionica, Sorina
KılıÇer, Pınar
Lauter, Kristin
Lorenzo GarcíA, Elisa
MÂnzĂŢeanu, Adelina
and
Vincent, Christelle
2024.
Determining the primes of bad reduction of cm curves of genus 3.
The Quarterly Journal of Mathematics,
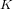 $K$, we give an explicit method for finding all genus-
$K$, we give an explicit method for finding all genus- $3$ hyperelliptic curves defined over
$3$ hyperelliptic curves defined over 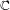 $\mathbb{C}$ whose Jacobians are simple and have complex multiplication by the maximal order of this field, via an approximation of their Rosenhain invariants. Building on the work of Weng [J. Ramanujan Math. Soc. 16 (2001) no. 4, 339–372], we give an algorithm which works in complete generality, for any CM sextic field
$\mathbb{C}$ whose Jacobians are simple and have complex multiplication by the maximal order of this field, via an approximation of their Rosenhain invariants. Building on the work of Weng [J. Ramanujan Math. Soc. 16 (2001) no. 4, 339–372], we give an algorithm which works in complete generality, for any CM sextic field  $K$, and computes minimal polynomials of the Rosenhain invariants for any period matrix of the Jacobian. This algorithm can be used to generate genus-3 hyperelliptic curves over a finite field
$K$, and computes minimal polynomials of the Rosenhain invariants for any period matrix of the Jacobian. This algorithm can be used to generate genus-3 hyperelliptic curves over a finite field 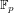 $\mathbb{F}_{p}$ with a given zeta function by finding roots of the Rosenhain minimal polynomials modulo
$\mathbb{F}_{p}$ with a given zeta function by finding roots of the Rosenhain minimal polynomials modulo  $p$.
$p$.



