No CrossRef data available.
Article contents
Computing cardinalities of 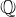 $\mathbb{Q}$-curve reductions over finite fields
$\mathbb{Q}$-curve reductions over finite fields
Published online by Cambridge University Press: 26 August 2016
Abstract
We present a specialized point-counting algorithm for a class of elliptic curves over 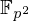 $\mathbb{F}_{p^{2}}$ that includes reductions of quadratic
$\mathbb{F}_{p^{2}}$ that includes reductions of quadratic 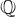 $\mathbb{Q}$-curves modulo inert primes and, more generally, any elliptic curve over
$\mathbb{Q}$-curves modulo inert primes and, more generally, any elliptic curve over 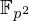 $\mathbb{F}_{p^{2}}$ with a low-degree isogeny to its Galois conjugate curve. These curves have interesting cryptographic applications. Our algorithm is a variant of the Schoof–Elkies–Atkin (SEA) algorithm, but with a new, lower-degree endomorphism in place of Frobenius. While it has the same asymptotic asymptotic complexity as SEA, our algorithm is much faster in practice.
$\mathbb{F}_{p^{2}}$ with a low-degree isogeny to its Galois conjugate curve. These curves have interesting cryptographic applications. Our algorithm is a variant of the Schoof–Elkies–Atkin (SEA) algorithm, but with a new, lower-degree endomorphism in place of Frobenius. While it has the same asymptotic asymptotic complexity as SEA, our algorithm is much faster in practice.
MSC classification
- Type
- Research Article
- Information
- LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 115 - 129
- Copyright
- © The Author(s) 2016




