No CrossRef data available.
Article contents
Computing boundary extensions of conformal maps
Published online by Cambridge University Press: 01 September 2014
Abstract
We show that a computable and conformal map of the unit disk onto a bounded domain 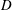 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}D$ has a computable boundary extension if
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}D$ has a computable boundary extension if 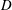 $D$ has a computable boundary connectivity function.
$D$ has a computable boundary connectivity function.
- Type
- Research Article
- Information
- Copyright
- © The Author 2014




