Article contents
An algorithm for NTRU problems and cryptanalysis of the GGH multilinear map without a low-level encoding of zero
Published online by Cambridge University Press: 26 August 2016
Abstract
Let 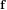 $\mathbf{f}$ and
$\mathbf{f}$ and  $\mathbf{g}$ be polynomials of a bounded Euclidean norm in the ring
$\mathbf{g}$ be polynomials of a bounded Euclidean norm in the ring 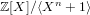 $\mathbb{Z}[X]/\langle X^{n}+1\rangle$. Given the polynomial
$\mathbb{Z}[X]/\langle X^{n}+1\rangle$. Given the polynomial 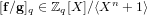 $[\mathbf{f}/\mathbf{g}]_{q}\in \mathbb{Z}_{q}[X]/\langle X^{n}+1\rangle$, the NTRU problem is to find
$[\mathbf{f}/\mathbf{g}]_{q}\in \mathbb{Z}_{q}[X]/\langle X^{n}+1\rangle$, the NTRU problem is to find 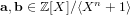 $\mathbf{a},\mathbf{b}\in \mathbb{Z}[X]/\langle X^{n}+1\rangle$ with a small Euclidean norm such that
$\mathbf{a},\mathbf{b}\in \mathbb{Z}[X]/\langle X^{n}+1\rangle$ with a small Euclidean norm such that 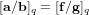 $[\mathbf{a}/\mathbf{b}]_{q}=[\mathbf{f}/\mathbf{g}]_{q}$. We propose an algorithm to solve the NTRU problem, which runs in
$[\mathbf{a}/\mathbf{b}]_{q}=[\mathbf{f}/\mathbf{g}]_{q}$. We propose an algorithm to solve the NTRU problem, which runs in 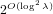 $2^{O(\log ^{2}\unicode[STIX]{x1D706})}$ time when
$2^{O(\log ^{2}\unicode[STIX]{x1D706})}$ time when 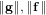 $\Vert \mathbf{g}\Vert ,\Vert \mathbf{f}\Vert$, and
$\Vert \mathbf{g}\Vert ,\Vert \mathbf{f}\Vert$, and 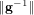 $\Vert \mathbf{g}^{-1}\Vert$ are within some range. The main technique of our algorithm is the reduction of a problem on a field to one on a subfield. The GGH scheme, the first candidate of an (approximate) multilinear map, was recently found to be insecure by the Hu–Jia attack using low-level encodings of zero, but no polynomial-time attack was known without them. In the GGH scheme without low-level encodings of zero, our algorithm can be directly applied to attack this scheme if we have some top-level encodings of zero and a known pair of plaintext and ciphertext. Using our algorithm, we can construct a level-
$\Vert \mathbf{g}^{-1}\Vert$ are within some range. The main technique of our algorithm is the reduction of a problem on a field to one on a subfield. The GGH scheme, the first candidate of an (approximate) multilinear map, was recently found to be insecure by the Hu–Jia attack using low-level encodings of zero, but no polynomial-time attack was known without them. In the GGH scheme without low-level encodings of zero, our algorithm can be directly applied to attack this scheme if we have some top-level encodings of zero and a known pair of plaintext and ciphertext. Using our algorithm, we can construct a level- $0$ encoding of zero and utilize it to attack a security ground of this scheme in the quasi-polynomial time of its security parameter using the parameters suggested by Garg, Gentry and Halevi [‘Candidate multilinear maps from ideal lattices’, Advances in cryptology — EUROCRYPT 2013 (Springer, 2013) 1–17].
$0$ encoding of zero and utilize it to attack a security ground of this scheme in the quasi-polynomial time of its security parameter using the parameters suggested by Garg, Gentry and Halevi [‘Candidate multilinear maps from ideal lattices’, Advances in cryptology — EUROCRYPT 2013 (Springer, 2013) 1–17].
MSC classification
- Type
- Research Article
- Information
- LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 255 - 266
- Copyright
- © The Author(s) 2016
References
- 66
- Cited by




