Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Harvey, David
Massierer, Maike
and
Sutherland, Andrew V.
2016.
Computing -series of geometrically hyperelliptic curves of genus three.
LMS Journal of Computation and Mathematics,
Vol. 19,
Issue. A,
p.
220.
Bisatt, Matthew
2019.
Explicit root numbers of abelian varieties.
Transactions of the American Mathematical Society,
Vol. 372,
Issue. 11,
p.
7889.
Farmer, David W.
Koutsoliotas, Sally
and
Lemurell, Stefan
2019.
Varieties via their L-functions.
Journal of Number Theory,
Vol. 196,
Issue. ,
p.
364.
Sutherland, Andrew V.
2019.
A database of nonhyperelliptic genus-3 curves
over ℚ.
The Open Book Series,
Vol. 2,
Issue. 1,
p.
443.
Bruin, Nils
Sijsling, Jeroen
and
Zotine, Alexandre
2019.
Numerical computation of endomorphism rings of Jacobians.
The Open Book Series,
Vol. 2,
Issue. 1,
p.
155.
Lairez, Pierre
and
Sertöz, Emre Can
2019.
A Numerical Transcendental Method in Algebraic Geometry: Computation of Picard Groups and Related Invariants.
SIAM Journal on Applied Algebra and Geometry,
Vol. 3,
Issue. 4,
p.
559.
Best, Alex J.
2021.
Arithmetic Geometry, Number Theory, and Computation.
p.
105.
Frutos-Fernández, María Inés de
and
Hashimoto, Sachi
2021.
Arithmetic Geometry, Number Theory, and Computation.
p.
449.
Cullinan, John
and
Zalesski, Alexandre
2021.
Unisingular representations in arithmetic and Lie theory.
European Journal of Mathematics,
Vol. 7,
Issue. 4,
p.
1645.
van Bommel, Raymond
2021.
Arithmetic Geometry, Number Theory, and Computation.
p.
237.
Patterson, S. J.
2021.
On a question of H. A. Schwarz.
Stochastics and Dynamics,
Vol. 21,
Issue. 03,
p.
2140004.
Berger, Tobias
and
Klosin, Krzysztof
2021.
Irreducibility of limits of Galois representations of Saito–Kurokawa type.
Research in Number Theory,
Vol. 7,
Issue. 3,
Mascot, Nicolas
Sijsling, Jeroen
and
Voight, John
2021.
Arithmetic Geometry, Number Theory, and Computation.
p.
559.
Cullinan, John
and
Yelton, Jeffrey
2022.
Divisibility of torsion subgroups of abelian surfaces over number fields.
Canadian Journal of Mathematics,
Vol. 74,
Issue. 1,
p.
266.
Hast, Daniel Rayor
2022.
Explicit two-cover descent for genus 2 curves.
Research in Number Theory,
Vol. 8,
Issue. 4,
van Bommel, Raymond
2022.
Numerical Verification of the Birch and Swinnerton-Dyer Conjecture for Hyperelliptic Curves of Higher Genus over ℚ up to Squares.
Experimental Mathematics,
Vol. 31,
Issue. 1,
p.
138.
He, Yang-Hui
Lee, Kyu-Hwan
and
Oliver, Thomas
2022.
Machine-learning the Sato–Tate conjecture.
Journal of Symbolic Computation,
Vol. 111,
Issue. ,
p.
61.
Kazalicki, Matija
and
Vlah, Domagoj
2023.
Ranks of elliptic curves and deep neural networks.
Research in Number Theory,
Vol. 9,
Issue. 3,
Müller, J. Steffen
and
Reitsma, Berno
2023.
Computing torsion subgroups of Jacobians of hyperelliptic curves of genus 3.
Research in Number Theory,
Vol. 9,
Issue. 2,
Elkies, Noam
2024.
LuCaNT: LMFDB, Computation, and Number Theory.
Vol. 796,
Issue. ,
p.
165.
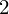 $2$ curves of small discriminant that includes geometric and arithmetic invariants of each curve, its Jacobian, and the associated
$2$ curves of small discriminant that includes geometric and arithmetic invariants of each curve, its Jacobian, and the associated 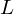 $L$-function. This data has been incorporated into the
$L$-function. This data has been incorporated into the 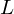 $L$-Functions and Modular Forms Database (LMFDB).
$L$-Functions and Modular Forms Database (LMFDB).



