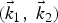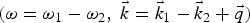1. INTRODUCTION
Compact powerful THz sources (0.1–10 THz) with fields as high as a few MV/cm (or power about GW/cm2) are desirable for scientific and commercial applications such as rapid two-dimensional imaging (Dragoman & Dragoman, Reference Dragoman and Dragoman2004), topography (Siegel, Reference Siegel2002), remote sensing (Sizov, Reference Sizov2010), chemical and security identification (Leemans et al., Reference Leemans, Geddes, Faure, Tóth, Tilborg, Schroeder, Esarey, Fubiani, Auerbach, Marcelis, Carnahan, Kaindl, Byrd and Martin2003), outer space communication and submillimeter radars (Schroeder et al., Reference Schroeder, Esarey, Tilborg and Leemans2004), imaging of biological tissue (Carr et al., Reference Carr, Martin, Mckinney, Jordan, Neil and Williams2002), spectroscopic identifications of complex molecules (Abo-Bakar et al., Reference Abo-Bakr, Feikes, Holldack, Kuske, Peatman, Schade, Wustefeld and Hübers2003), explosive detection (Yoshii et al., 1997), etc. It is difficult to obtain such powerful THz emitters utilizing electro-optic crystals (Hamester et al., Reference Hamster, Sullivan, Gordon, White and Falcone1993; Reference Hamster, Sullivan, Gordon and Falcone1994), semiconductors (Schillinger & Sauerbrey, Reference Schillinger and Sauerbrey1999), photoconductive antennas (Sprangle et al., Reference Sprangle, Penano, Hafizi and Kapetanakos2004), etc., due to the breakdown limit and low conversion efficiencies. To address these issues, plasma based THz emitters utilizing electron beams and laser plasma interaction were proposed such as coherent radiation from plasma oscillations driven by ultra-short laser pulses (Antonesen et al., 2006), synchrotron radiation from accelerated electrons (Liu et al., Reference Liu and Tripathi2009), and transition radiation of electron beams (Sheng et al., Reference Sheng, Wu, Li and Zhang2004) etc. In these schemes, plasma as a nonlinear medium can handle very high power lasers with an added advantage of not having damage limit (Sheng et al., Reference Sheng, Mima and Zhang2005; Kumar & Tripathi, Reference Kumar and Tripathi2013; Verma & Sharma, Reference Verma and Sharma2009; Giulietti et al., Reference Giulietti, Banfi, Deha, Giulietti, Lucchesi, Nocera and Zun1988; Panwar et al., Reference Panwar, Ryu and Kumar2013; Ghorbanalilu, Reference Ghorbanalilu2012; Garg & Tripathi, Reference Garg and Tripathi2010; Verma & Sharma, Reference Verma and Sharma2011).
Recently, various experiments based on laser beating (one of fundamental and other at second harmonics) in plasmas have reported efficient THz radiation generation (Esarey et al., Reference Esarey, Sprangle, Krall and Ting1996; D'Amico et al., Reference D'amico, Houard, Franco, Prade, Mysyrowicz, Couairon and Tikhonchuk2007; Tani et al., Reference Tani, Gu, Hyodo, Sakai and Hidaka2000; Xie et al., Reference Xie, Dai and Zhang2006; Bhasin & Tripathi, 2009; Tripathi & Liu, Reference Tripathi and Liu1990; Liu & Tripathi, Reference Liu and Tripathi2009; Dua et al., Reference Dua, Chena, Shenga and Zhanga2011; Hu et al., Reference Hu, Shen, Lei, Li and Xu2010; Varshney et al., Reference Varshney, Sajal, Chauhan, Kumar and Sharma2014). Out of various schemes based on laser plasma interaction, THz radiation generation by beating of two lasers of different frequencies and wave numbers in plasmas has shown tremendous potential in terms of amplitude, tunability, efficiency, and directionality (Varshney et al., Reference Varshney, Sajal, Singh, Kumar and Sharma2013; Reference Varshney, Sajal, Chauhan, Kumar and Sharma2014; Nafil et al., Reference Nafil, Singh, Al-Janabi and Sharma2013; Malik et al., Reference Malik, Malik and Stroth2012; Reference Malik, Malik and Nishida2011; Malik & Malik, Reference Malik and Malik2012). THz sources based on beating can also be scaled to high peak powers. Xie et al. (Reference Xie, Dai and Zhang2006) observed that properties of emitted THz radiation are consistent with four waves mixing in plasma, and THz emission is maximized when the polarization of the laser beams and the THz are aligned. Bhasin and Tripathi (Reference Bhasin and Tripathi2011) and Varshney et al. (Reference Varshney, Sajal, Singh, Kumar and Sharma2013) have examined resonant THz radiation generation by beating of x-polarized laser beams in rippled density magnetized plasma.
Different types of laser profiles (Nafil et al., Reference Nafil, Singh, Al-Janabi and Sharma2013, Malik et al., Reference Malik, Malik and Stroth2012; Reference Malik, Malik and Nishida2011) were utilized by various researchers to enhance amplitude and power of THz radiation in various beat wave schemes in plasmas. Malik et al. (Reference Malik, Malik and Stroth2012) utilized the Gaussian profile of beating lasers in periodic density rippled plasma and realized efficiency and 10−3 for the laser intensity of about 1014 W/cm2. The efficiency is improved to about 0.006 by replacing the Gaussian profile by super Gaussian profile (Malik & Malik, Reference Malik and Malik2012) of beating lasers for same parameters. They concluded that the two spatial super Gaussian lasers of higher index and smaller beam width can produce much stronger THz radiation compared to the case of Gaussian lasers. The radiation can also be focused at a desired position along with more collimation by varying of the index of lasers in plasma having larger density ripples. Malik et al. (Reference Malik, Malik and Stroth2012) have achieved efficiency about 10−2 by beating of spatial triangular lasers in plasma for the laser intensity about 1014 W/Cm2, at the THz field about 105 kV/cm.
In the present work, we propose a scheme of resonant THz radiation generation by beating of two extraordinary lasers (with triangular envelopes in space) co-propagating in a plasma having periodically modulated density ripples. The issue of high amplitude and power of THz radiation is addressed by employing triangular profiles and x-mode polarization of lasers. Both the beating lasers and generated THz radiation have the same state of polarization because the THz emission is maximized when the polarization of laser beams and the THz are aligned (Malik et al., Reference Malik, Malik and Stroth2012). Issues of directionality and tunability are addressed by applying dc static magnetic field in transverse direction. Two co-propagating x-mode triangular shaped [(![]() ${\rm \omega} _1 \comma \; \vec k_1 $) and (
${\rm \omega} _1 \comma \; \vec k_1 $) and (![]() ${\rm \omega} _2 \comma \; \vec k_2 $)] (Fig. 1) exert a nonlinear ponderomotive force at frequency ω = ω1 − ω2 and wave number
${\rm \omega} _2 \comma \; \vec k_2 $)] (Fig. 1) exert a nonlinear ponderomotive force at frequency ω = ω1 − ω2 and wave number ![]() $\vec k = \vec k_1 - \vec k_2 $ on plasma electrons. Velocity perturbation due to ponderomotive forces couples with density ripples of appropriate periodicity and excites a nonlinear current. The nonlinear current can excite THz radiation if resonance conditions are simultaneously satisfied. In Section 2, expressions of ponderomotive force, density perturbation and nonlinear current density are derived. The amplitude and efficiency of THz wave are calculated in Section 3. Discussion on results is given in the Section 4.
$\vec k = \vec k_1 - \vec k_2 $ on plasma electrons. Velocity perturbation due to ponderomotive forces couples with density ripples of appropriate periodicity and excites a nonlinear current. The nonlinear current can excite THz radiation if resonance conditions are simultaneously satisfied. In Section 2, expressions of ponderomotive force, density perturbation and nonlinear current density are derived. The amplitude and efficiency of THz wave are calculated in Section 3. Discussion on results is given in the Section 4.

Fig. 1. Schematic diagram of terahertz radiation generation by beating of two x-mode lasers.
2. NONLINEAR CURRENT DUE TO BEATING OF LASERS
Consider a laser produced rippled plasma of density n ≡ n 0 + n′, n′ = n q0e iqz with static magnetic field ![]() $\vec B_0 $ in
$\vec B_0 $ in ![]() $\hat x$ direction, where n q0 as the amplitude of ripple and q as the wave vector of density ripples. Plasma density ripples can be produced using various techniques involving transmission ring grating and patterned mask, where the control of ripple parameters might be possible by changing groove period, groove structure, and duty cycle in such a grating, and by adjusting the period and the size of mask (Malik & Malik, Reference Malik, Malik and Stroth2012; Penano et al., Reference Penano, Sprangle, Hafizi, Gordo and Serafim2010). Two x-mode spatial triangular lasers co-propagate through it along
$\hat x$ direction, where n q0 as the amplitude of ripple and q as the wave vector of density ripples. Plasma density ripples can be produced using various techniques involving transmission ring grating and patterned mask, where the control of ripple parameters might be possible by changing groove period, groove structure, and duty cycle in such a grating, and by adjusting the period and the size of mask (Malik & Malik, Reference Malik, Malik and Stroth2012; Penano et al., Reference Penano, Sprangle, Hafizi, Gordo and Serafim2010). Two x-mode spatial triangular lasers co-propagate through it along ![]() $\hat z$-direction having electric field profile (Malik et al., Reference Malik, Malik and Stroth2012):
$\hat z$-direction having electric field profile (Malik et al., Reference Malik, Malik and Stroth2012):
where E 002 = A 02(1 − |y/a 0|)2, for |y/a 0| < 1 and zero otherwise; j = 1, 2; 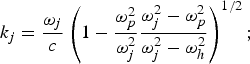 $k_j = \displaystyle{{{\rm \omega} _j } \over c}\left({1 - \displaystyle{{{\rm \omega} _p^2 } \over {{\rm \omega} _j^2 }}\displaystyle{{{\rm \omega} _j^2 - {\rm \omega} _p^2 } \over {{\rm \omega} _j^2 - {\rm \omega} _h^2 }}} \right)^{1/2}; $a 0 is the beam width parameter of lasers, ωh2 = ωp2 + ωc2, ωp2 = 4πn 0e 2/m and ωc = eB 0/m are upper hybrid frequency, electron plasma frequency, and cyclotron frequency, respectively; −e and m are the electronic charge and mass; and εjzz = [1 − ωp2/(ωj2 − ωc2)] & εjzy = −i[ωcωp2/ωj(ωj2 − ωc2)] are components of the dielectric tensor εj. Extraordinary mode or x-mode is the natural electromagnetic mode of magnetized plasma.
$k_j = \displaystyle{{{\rm \omega} _j } \over c}\left({1 - \displaystyle{{{\rm \omega} _p^2 } \over {{\rm \omega} _j^2 }}\displaystyle{{{\rm \omega} _j^2 - {\rm \omega} _p^2 } \over {{\rm \omega} _j^2 - {\rm \omega} _h^2 }}} \right)^{1/2}; $a 0 is the beam width parameter of lasers, ωh2 = ωp2 + ωc2, ωp2 = 4πn 0e 2/m and ωc = eB 0/m are upper hybrid frequency, electron plasma frequency, and cyclotron frequency, respectively; −e and m are the electronic charge and mass; and εjzz = [1 − ωp2/(ωj2 − ωc2)] & εjzy = −i[ωcωp2/ωj(ωj2 − ωc2)] are components of the dielectric tensor εj. Extraordinary mode or x-mode is the natural electromagnetic mode of magnetized plasma.
If the electric field of propagating laser ![]() $\vec E_j = \hat yE_{00} \, e^{ - i\lpar {\rm \omega} _j t - k_j z\rpar }$ in a plasma is perpendicular to applied dc magnetic field
$\vec E_j = \hat yE_{00} \, e^{ - i\lpar {\rm \omega} _j t - k_j z\rpar }$ in a plasma is perpendicular to applied dc magnetic field ![]() $\vec B_0 = {B}_0 \hat x$, then the plasma electron motion will also be affected by
$\vec B_0 = {B}_0 \hat x$, then the plasma electron motion will also be affected by ![]() $ - e\lpar \vec v \times \vec B_o \rpar $ force due to applied magnetic field and the dispersion relation will be changed. As a result, a longitudinal component develops and laser becomes partly longitudinal and partly transverse. These two components are related to each other by the expression E z = −(εjzy/εjzz)E y. This expression has the signature of applied dc magnetic field (Chen, Reference Chen1983). These extraordinary modes of electromagnetic waves are extensively utilized in magnetized plasma for various purposes like parametric instabilities, electron acceleration, harmonic generation, etc. Here, lasers impart oscillatory velocity to plasma electrons in
$ - e\lpar \vec v \times \vec B_o \rpar $ force due to applied magnetic field and the dispersion relation will be changed. As a result, a longitudinal component develops and laser becomes partly longitudinal and partly transverse. These two components are related to each other by the expression E z = −(εjzy/εjzz)E y. This expression has the signature of applied dc magnetic field (Chen, Reference Chen1983). These extraordinary modes of electromagnetic waves are extensively utilized in magnetized plasma for various purposes like parametric instabilities, electron acceleration, harmonic generation, etc. Here, lasers impart oscillatory velocity to plasma electrons in ![]() $\hat y$ and
$\hat y$ and ![]() ${\hat {\rm z}}$ direction, given by
${\hat {\rm z}}$ direction, given by
 $$v_{jy} = \displaystyle{e \over {m\lpar {\rm \omega} _j^2 - {\rm \omega} _c^2 \rpar }}\left[{i{\rm \omega} _j^{} + {\rm \omega} _c^{} \displaystyle{{{\rm \varepsilon} _{\,jzy} } \over {{\rm \varepsilon} _{\,jzz} }}} \right]E_{00} e^{ - i\lpar {\rm \omega} _j t - k_j z\rpar }\comma \;$$
$$v_{jy} = \displaystyle{e \over {m\lpar {\rm \omega} _j^2 - {\rm \omega} _c^2 \rpar }}\left[{i{\rm \omega} _j^{} + {\rm \omega} _c^{} \displaystyle{{{\rm \varepsilon} _{\,jzy} } \over {{\rm \varepsilon} _{\,jzz} }}} \right]E_{00} e^{ - i\lpar {\rm \omega} _j t - k_j z\rpar }\comma \;$$ $$v_{\,jz} = \displaystyle{e \over {m\lpar {\rm \omega} _j^2 - {\rm \omega} _c^2 \rpar }}\left[{{\rm \omega} _c^{} + i{\rm \omega} _j^{} \displaystyle{{{\rm \varepsilon} _{\,jzy} } \over {{\rm \varepsilon} _{\,jzz} }}} \right]E_{00} e^{ - i\lpar {\rm \omega} _j t - k_j z\rpar }.$$
$$v_{\,jz} = \displaystyle{e \over {m\lpar {\rm \omega} _j^2 - {\rm \omega} _c^2 \rpar }}\left[{{\rm \omega} _c^{} + i{\rm \omega} _j^{} \displaystyle{{{\rm \varepsilon} _{\,jzy} } \over {{\rm \varepsilon} _{\,jzz} }}} \right]E_{00} e^{ - i\lpar {\rm \omega} _j t - k_j z\rpar }.$$ Lasers beat together and exert a ponderomotive force ![]() $\vec F_{p}\lpar =F_{\,py} \hat y + F_{pz} \hat z\rpar $ on plasma electron at frequency ω = ω1 − ω2 and wave vector
$\vec F_{p}\lpar =F_{\,py} \hat y + F_{pz} \hat z\rpar $ on plasma electron at frequency ω = ω1 − ω2 and wave vector ![]() $\vec k = \vec k_1 - \vec k_2$. The components of the ponderomotive force F py and F pz are as follows:
$\vec k = \vec k_1 - \vec k_2$. The components of the ponderomotive force F py and F pz are as follows:
 $$\eqalign{F_{py} &= \displaystyle{e^2 \over 2m} \left[\displaystyle{1 \over \lpar {\rm \omega}_1^2 - {\rm \omega} _c^2 \rpar \, \lpar {\rm \omega} _2^2 - {\rm \omega} _c^2 \rpar} \left\{\displaystyle{2 \over a_0 \left(1 - \left\vert y / a_0 \right\vert \right)} \right. \right. \cr & \quad \times \left(i{\rm \omega}_1 + {\rm \omega}_c \displaystyle{{\rm \varepsilon}_{1zy} \over {\rm \varepsilon}_{1zz}} \right)\, \left( - i{\rm \omega} _2 + {\rm \omega}_c \displaystyle{{\rm \varepsilon}_{2zy} \over {\rm \varepsilon}_{2zz}} \right) + ik_2 \left({\rm \omega}_c + i{\rm \omega}_1 \displaystyle{{\rm \varepsilon} _{1zy} \over {\rm \varepsilon}_{1zz}} \right) \cr & \quad \times \left. \left( - i{\rm \omega} _2 + {\rm \omega} _c \displaystyle{{\rm \varepsilon} _{2zy} \over {\rm \varepsilon}_{2zz}} \right)- ik_1 \left(i{\rm \omega} _1 + {\rm \omega}_c \displaystyle{{\rm \varepsilon}_{1zy} \over {\rm \varepsilon}_{1zz}} \right) + \, \left({\rm \omega}_c - i{\rm \omega} _2 \displaystyle{{\rm \varepsilon}_{2zy} \over {\rm \varepsilon}_{2zz}} \right) \right\} \cr & \quad \left. + \displaystyle{k_2 \left({\rm \omega}_c + i\displaystyle{{\rm \varepsilon}_{1zy} \over {\rm \varepsilon}_{1zz}} {\rm \omega}_1 \right) \over {\rm \omega} _2 \lpar {\rm \omega} _1^2 - {\rm \omega} _c^2 \rpar} + \displaystyle{k_1 \left({\rm \omega}_c - i \displaystyle{{\rm \varepsilon} _{2zy} \over {\rm \varepsilon}_{2zz}} {\rm \omega}_2 \right) \over {\rm \omega}_1 \lpar {\rm \omega}_2^2 - {\rm \omega} _c^2 \rpar} \right]\, E_{00}^2 \, e^{ - i\lpar {\rm \omega} t - kz\rpar}\comma} \;$$
$$\eqalign{F_{py} &= \displaystyle{e^2 \over 2m} \left[\displaystyle{1 \over \lpar {\rm \omega}_1^2 - {\rm \omega} _c^2 \rpar \, \lpar {\rm \omega} _2^2 - {\rm \omega} _c^2 \rpar} \left\{\displaystyle{2 \over a_0 \left(1 - \left\vert y / a_0 \right\vert \right)} \right. \right. \cr & \quad \times \left(i{\rm \omega}_1 + {\rm \omega}_c \displaystyle{{\rm \varepsilon}_{1zy} \over {\rm \varepsilon}_{1zz}} \right)\, \left( - i{\rm \omega} _2 + {\rm \omega}_c \displaystyle{{\rm \varepsilon}_{2zy} \over {\rm \varepsilon}_{2zz}} \right) + ik_2 \left({\rm \omega}_c + i{\rm \omega}_1 \displaystyle{{\rm \varepsilon} _{1zy} \over {\rm \varepsilon}_{1zz}} \right) \cr & \quad \times \left. \left( - i{\rm \omega} _2 + {\rm \omega} _c \displaystyle{{\rm \varepsilon} _{2zy} \over {\rm \varepsilon}_{2zz}} \right)- ik_1 \left(i{\rm \omega} _1 + {\rm \omega}_c \displaystyle{{\rm \varepsilon}_{1zy} \over {\rm \varepsilon}_{1zz}} \right) + \, \left({\rm \omega}_c - i{\rm \omega} _2 \displaystyle{{\rm \varepsilon}_{2zy} \over {\rm \varepsilon}_{2zz}} \right) \right\} \cr & \quad \left. + \displaystyle{k_2 \left({\rm \omega}_c + i\displaystyle{{\rm \varepsilon}_{1zy} \over {\rm \varepsilon}_{1zz}} {\rm \omega}_1 \right) \over {\rm \omega} _2 \lpar {\rm \omega} _1^2 - {\rm \omega} _c^2 \rpar} + \displaystyle{k_1 \left({\rm \omega}_c - i \displaystyle{{\rm \varepsilon} _{2zy} \over {\rm \varepsilon}_{2zz}} {\rm \omega}_2 \right) \over {\rm \omega}_1 \lpar {\rm \omega}_2^2 - {\rm \omega} _c^2 \rpar} \right]\, E_{00}^2 \, e^{ - i\lpar {\rm \omega} t - kz\rpar}\comma} \;$$ $$\eqalign{F_{pz} &= \displaystyle{e^2 \over 2m} \left[\displaystyle{1 \over \lpar {\rm \omega}_1^2 - {\rm \omega} _c^2 \rpar \lpar {\rm \omega}_2^2 - {\rm \omega} _c^2 \rpar} \left\{\displaystyle{1 \over a_0 \left(1 - \left\vert y / a_0 \right\vert \right)} \left(i{\rm \omega}_1 + {\rm \omega}_c \displaystyle{{\rm \varepsilon}_{1zy} \over {\rm \varepsilon}_{1zz}} \right)\right. \right. \cr & \quad \times \left({\rm \omega}_c - i{\rm \omega}_2 \displaystyle{{\rm \varepsilon}_{2zy} \over {\rm \varepsilon}_{2zz}} \right) + \displaystyle{1 \over a_0 \left(1 - \left\vert y / a_0 \right\vert \right)} \left( - i{\rm \omega}_2 + {\rm \omega}_c \displaystyle{{\rm \varepsilon}_{2zy} \over {\rm \varepsilon}_{2zz}} \right) \cr & \quad \times \left. \left({\rm \omega} _c + i{\rm \omega} _1 \displaystyle{{\rm \varepsilon} _{1zy} \over {\rm \varepsilon}_{1zz}} \right)- ik \left({\rm \omega}_c + i{\rm \omega} _1 \displaystyle{{\rm \varepsilon}_{1zy} \over {\rm \varepsilon}_{1zz}} \right) \left({\rm \omega}_c - i{\rm \omega}_2 \displaystyle{{\rm \varepsilon}_{2zy} \over {\rm \varepsilon}_{2zz}} \right) \right\}\cr & \quad + \left. \displaystyle{k_2 \left(i {\rm \omega}_1 + {\rm \omega}_c \displaystyle{{\rm \varepsilon}_{1zy} \over {\rm \varepsilon}_{1zz}} \right) \over {\rm \omega}_2 \lpar {\rm \omega}_1^2 - {\rm \omega}_c^2 \rpar} + \displaystyle{k_1 \left( - i{\rm \omega} _2 + {\rm \omega}_c \displaystyle{{\rm \varepsilon}_{2zy} \over {\rm \varepsilon}_{2zz}} \right) \over {\rm \omega}_1 \lpar {\rm \omega}_2^2 - {\rm \omega}_c^2 \rpar} \right]\, E_{00}^2 \, e^{ - i\lpar {\rm \omega} t - kz\rpar}.}$$
$$\eqalign{F_{pz} &= \displaystyle{e^2 \over 2m} \left[\displaystyle{1 \over \lpar {\rm \omega}_1^2 - {\rm \omega} _c^2 \rpar \lpar {\rm \omega}_2^2 - {\rm \omega} _c^2 \rpar} \left\{\displaystyle{1 \over a_0 \left(1 - \left\vert y / a_0 \right\vert \right)} \left(i{\rm \omega}_1 + {\rm \omega}_c \displaystyle{{\rm \varepsilon}_{1zy} \over {\rm \varepsilon}_{1zz}} \right)\right. \right. \cr & \quad \times \left({\rm \omega}_c - i{\rm \omega}_2 \displaystyle{{\rm \varepsilon}_{2zy} \over {\rm \varepsilon}_{2zz}} \right) + \displaystyle{1 \over a_0 \left(1 - \left\vert y / a_0 \right\vert \right)} \left( - i{\rm \omega}_2 + {\rm \omega}_c \displaystyle{{\rm \varepsilon}_{2zy} \over {\rm \varepsilon}_{2zz}} \right) \cr & \quad \times \left. \left({\rm \omega} _c + i{\rm \omega} _1 \displaystyle{{\rm \varepsilon} _{1zy} \over {\rm \varepsilon}_{1zz}} \right)- ik \left({\rm \omega}_c + i{\rm \omega} _1 \displaystyle{{\rm \varepsilon}_{1zy} \over {\rm \varepsilon}_{1zz}} \right) \left({\rm \omega}_c - i{\rm \omega}_2 \displaystyle{{\rm \varepsilon}_{2zy} \over {\rm \varepsilon}_{2zz}} \right) \right\}\cr & \quad + \left. \displaystyle{k_2 \left(i {\rm \omega}_1 + {\rm \omega}_c \displaystyle{{\rm \varepsilon}_{1zy} \over {\rm \varepsilon}_{1zz}} \right) \over {\rm \omega}_2 \lpar {\rm \omega}_1^2 - {\rm \omega}_c^2 \rpar} + \displaystyle{k_1 \left( - i{\rm \omega} _2 + {\rm \omega}_c \displaystyle{{\rm \varepsilon}_{2zy} \over {\rm \varepsilon}_{2zz}} \right) \over {\rm \omega}_1 \lpar {\rm \omega}_2^2 - {\rm \omega}_c^2 \rpar} \right]\, E_{00}^2 \, e^{ - i\lpar {\rm \omega} t - kz\rpar}.}$$ The ponderomotive force drives space charge oscillation at ![]() ${\rm \omega} = {\rm \omega} _1 - {\rm \omega} _2 $ and wave number
${\rm \omega} = {\rm \omega} _1 - {\rm \omega} _2 $ and wave number ![]() $\vec k_1 - \vec k_2 $. Assuming the potential of space charge mode to be ϕ, the oscillatory velocity of electron due to space charge mode along with ponderomotive force in the presence of static magnetic field can be expressed as follows:
$\vec k_1 - \vec k_2 $. Assuming the potential of space charge mode to be ϕ, the oscillatory velocity of electron due to space charge mode along with ponderomotive force in the presence of static magnetic field can be expressed as follows:
The nonlinear velocity given by Eq. (5) along with continuity equation provide density perturbation n = n L + n NL, where
and χ = −ωp2/(ω2 − ωc2). Linear density perturbation (n L) is induced self-consistently by space charge field and nonlinear density perturbation (n NL) is the consequence of ponderomotive force. Here, density perturbation is assumed to be small as compared to the density ripple. Substituting n = n L + n NL in the Poisson's equation ∇2φ = 4πne, we obtain
where, ε = 1 + χ. Combining Eqs. (6)–(8), we have,
Substituting this value of ϕ in Eq. (5), we obtain the oscillatory velocity components of plasma electrons:
 $$v_z = \displaystyle{{{\rm \omega} _c } \over {m\lpar {\rm \omega} ^2 - {\rm \omega} _h^2 \rpar }}F_{\!pz} + i\displaystyle{{\lpar {\rm \omega} ^2 - {\rm \omega} _p^2 \rpar } \over {m\lpar {\rm \omega} ^2 - {\rm \omega} _h^2 \rpar {\rm \omega} }}F_{\!py}.$$
$$v_z = \displaystyle{{{\rm \omega} _c } \over {m\lpar {\rm \omega} ^2 - {\rm \omega} _h^2 \rpar }}F_{\!pz} + i\displaystyle{{\lpar {\rm \omega} ^2 - {\rm \omega} _p^2 \rpar } \over {m\lpar {\rm \omega} ^2 - {\rm \omega} _h^2 \rpar {\rm \omega} }}F_{\!py}.$$ Oscillations at ![]() $\lpar {\rm \omega} \comma \; \vec k_1 - \vec k_2 \rpar $ in the presence of density ripple n qoe iqz excite nonlinear current at
$\lpar {\rm \omega} \comma \; \vec k_1 - \vec k_2 \rpar $ in the presence of density ripple n qoe iqz excite nonlinear current at ![]() $\lpar {\rm \omega} \comma \; \vec k_1 - \vec k_2 + \vec q\rpar $ which can be written as
$\lpar {\rm \omega} \comma \; \vec k_1 - \vec k_2 + \vec q\rpar $ which can be written as
This oscillatory current is the source for the emission of THz radiation at the beating frequency ω which is the same as that of the ponderomotive force but its wave number is different. For strong THz radiation, plasma density ripples should be periodic, otherwise ![]() $\vec k\lpar\! = \vec k_1 - \vec k_2 + \vec q\rpar $ will exhibit non-periodic behavior; resonance condition can't be achieved and maximum energy transfer will not take place and consequently a weak field THz radiation will be generated.
$\vec k\lpar\! = \vec k_1 - \vec k_2 + \vec q\rpar $ will exhibit non-periodic behavior; resonance condition can't be achieved and maximum energy transfer will not take place and consequently a weak field THz radiation will be generated.
3. THZ RADIATION AMPLITUDE
The following wave equation is solved to find the amplitude of the THz wave
where, ε is the plasma permittivity tensor at ω. Taking fast phase variations in the electric field profile of THz radiation as ![]() $\vec E = \vec A\lpar z\rpar e^{ - i\lpar {\rm \omega} t - kz\rpar } $, the wave equation (Eq. (12)) governing the propagation of THz waves can be split into
$\vec E = \vec A\lpar z\rpar e^{ - i\lpar {\rm \omega} t - kz\rpar } $, the wave equation (Eq. (12)) governing the propagation of THz waves can be split into ![]() $\hat y$ and
$\hat y$ and ![]() $\hat z$ components as follows:
$\hat z$ components as follows:
The excited THz mode will have same polarization state as the beating lasers. It will have both y- and z-components of electric field corresponding to its x-mode nature. These components will be related to Eq. (12a). Xie et al. (Reference Xie, Dai and Zhang2006) also observed that THz emission will be maximized when the polarization of laser beams and the THz are aligned. By rearranging Eq. (12a) and Eq. (12b), we obtained the equation governing transverse component A y of THz radiation. Longitudinal component of THz can be calculated by Eq. (12b)
 $$- 2ik\displaystyle{{\partial A_y } \over {\partial z}} + \left({k^2 - \displaystyle{{{\rm \omega} ^2 } \over {c^2 }}{\rm \varepsilon} _{yy} + \displaystyle{{{\rm \omega} ^2 } \over {c^2 }}\displaystyle{{{\rm \varepsilon} _{yz} {\rm \varepsilon} _{zy} } \over {{\rm \varepsilon} _{zz} }}} \right)A_y = + \displaystyle{{4{\rm \pi} i{\rm \omega} } \over {c^2 }}J_y^{NL} - \displaystyle{{{\rm \varepsilon} _{yz} } \over {{\rm \varepsilon} _{zz} }}\displaystyle{{4{\rm \pi} i{\rm \omega} } \over {c^2 }}J_z^{NL}.$$
$$- 2ik\displaystyle{{\partial A_y } \over {\partial z}} + \left({k^2 - \displaystyle{{{\rm \omega} ^2 } \over {c^2 }}{\rm \varepsilon} _{yy} + \displaystyle{{{\rm \omega} ^2 } \over {c^2 }}\displaystyle{{{\rm \varepsilon} _{yz} {\rm \varepsilon} _{zy} } \over {{\rm \varepsilon} _{zz} }}} \right)A_y = + \displaystyle{{4{\rm \pi} i{\rm \omega} } \over {c^2 }}J_y^{NL} - \displaystyle{{{\rm \varepsilon} _{yz} } \over {{\rm \varepsilon} _{zz} }}\displaystyle{{4{\rm \pi} i{\rm \omega} } \over {c^2 }}J_z^{NL}.$$From Eq. (13), one can observe that resonant THz radiation generation demands to satisfy the following dispersion relation for exact phase matching condition in rippled magnetized plasma which provides the periodicity of rippled structure and suggests that the maximum energy transfer from beating lasers to THz radiation will take place at resonance condition:
Substituting the phase matching condition in Eq. (13), we obtain the amplitude of THz radiation as follows:
 $$\eqalign{\left\vert {A_y } \right\vert &= \displaystyle{1 \over {4k}}\displaystyle{{n_{q0} } \over {n_0 }}\displaystyle{{{\rm \omega} {\rm \omega} _p^2 } \over {{\rm \omega} ^2 - {\rm \omega} _h^2 }}\displaystyle{z \over {ec^2 }}\left[{i\left({\displaystyle{{{\rm \omega} ^2 - {\rm \omega} _p^2 } \over {\rm \omega} } - \left\vert {\displaystyle{{{\rm \varepsilon} _{zy} } \over {{\rm \varepsilon} _{zz} }}} \right\vert {\rm \omega} _c } \right)F_{\!py}}\right. \cr&\left.\quad+ \left({{\rm \omega} _c - {\rm \omega} \left\vert {\displaystyle{{{\rm \varepsilon} _{zy} } \over {{\rm \varepsilon} _{zz} }}} \right\vert } \right)F_{\!pz} \right].}$$
$$\eqalign{\left\vert {A_y } \right\vert &= \displaystyle{1 \over {4k}}\displaystyle{{n_{q0} } \over {n_0 }}\displaystyle{{{\rm \omega} {\rm \omega} _p^2 } \over {{\rm \omega} ^2 - {\rm \omega} _h^2 }}\displaystyle{z \over {ec^2 }}\left[{i\left({\displaystyle{{{\rm \omega} ^2 - {\rm \omega} _p^2 } \over {\rm \omega} } - \left\vert {\displaystyle{{{\rm \varepsilon} _{zy} } \over {{\rm \varepsilon} _{zz} }}} \right\vert {\rm \omega} _c } \right)F_{\!py}}\right. \cr&\left.\quad+ \left({{\rm \omega} _c - {\rm \omega} \left\vert {\displaystyle{{{\rm \varepsilon} _{zy} } \over {{\rm \varepsilon} _{zz} }}} \right\vert } \right)F_{\!pz} \right].}$$The normalized amplitude of THz radiation can be written as follows:
 $$\eqalign{ \left\vert {\displaystyle{{A_y } \over {A_0 }}} \right\vert &= \displaystyle{1 \over {4k}}\displaystyle{{n_{q0} } \over {n_0 }}\displaystyle{1 \over {{\rm \omega} \lpar {\rm \omega} ^2 - {\rm \omega} _h^2 \rpar }}z\bigg[{\left({\displaystyle{{{\rm \omega} ^2 - 1} \over {\rm \omega} } - \left\vert {\displaystyle{{{\rm \varepsilon} _{zy} } \over {{\rm \varepsilon} _{zz} }}} \right\vert {\rm \omega} _c } \right)f_{\!py}} \cr & \quad + \left({{\rm \omega} _c - {\rm \omega} \left\vert {\displaystyle{{{\rm \varepsilon} _{zy} } \over {{\rm \varepsilon} _{zz} }}} \right\vert } \right)f_{\!pz} \bigg]\comma \;}$$
$$\eqalign{ \left\vert {\displaystyle{{A_y } \over {A_0 }}} \right\vert &= \displaystyle{1 \over {4k}}\displaystyle{{n_{q0} } \over {n_0 }}\displaystyle{1 \over {{\rm \omega} \lpar {\rm \omega} ^2 - {\rm \omega} _h^2 \rpar }}z\bigg[{\left({\displaystyle{{{\rm \omega} ^2 - 1} \over {\rm \omega} } - \left\vert {\displaystyle{{{\rm \varepsilon} _{zy} } \over {{\rm \varepsilon} _{zz} }}} \right\vert {\rm \omega} _c } \right)f_{\!py}} \cr & \quad + \left({{\rm \omega} _c - {\rm \omega} \left\vert {\displaystyle{{{\rm \varepsilon} _{zy} } \over {{\rm \varepsilon} _{zz} }}} \right\vert } \right)f_{\!pz} \bigg]\comma \;}$$
where f pz = iF pz and f py = iF py. Eq. (16) reveals that the normalized THz amplitude is directly proportional to the normalized amplitude of density ripples n q0/n 0, thus THz field increases on increasing ripple amplitude. Its explanation lies in Eq. (11); higher the ripple amplitude, greater the number of electrons involving in the generation of oscillatory nonlinear current. Higher number of charge carriers results into higher nonlinear current (![]() $\vec J^{NL} $) leading to more efficient THz radiation.
$\vec J^{NL} $) leading to more efficient THz radiation.
The phase matching condition ![]() $q = \lpar {\rm \omega} /c\rpar \vert {\rm \varepsilon} _{yy} + \lpar {\rm \varepsilon} _{xy} {\rm \varepsilon} _{yx} /$
$q = \lpar {\rm \omega} /c\rpar \vert {\rm \varepsilon} _{yy} + \lpar {\rm \varepsilon} _{xy} {\rm \varepsilon} _{yx} /$![]() ${\rm \varepsilon} _{xx} \rpar ^{1/2} - 1\vert $ for resonant excitation of THz radiation provides the estimate of periodicity of rippled structure for maximum energy transfer in this process. In Figure 2, normalized periodicity factor (cq/ωp) of density rippled structure is plotted as a function of normalized THz frequency (ω/ωp) and normalized cyclotron frequency (ωc/ωp). Periodicity factor (q) decreases with THz wave frequency, increases with applied magnetic field and achieves maximum value as THz frequency (ω) approaches toward resonance value
${\rm \varepsilon} _{xx} \rpar ^{1/2} - 1\vert $ for resonant excitation of THz radiation provides the estimate of periodicity of rippled structure for maximum energy transfer in this process. In Figure 2, normalized periodicity factor (cq/ωp) of density rippled structure is plotted as a function of normalized THz frequency (ω/ωp) and normalized cyclotron frequency (ωc/ωp). Periodicity factor (q) decreases with THz wave frequency, increases with applied magnetic field and achieves maximum value as THz frequency (ω) approaches toward resonance value ![]() ${\rm \omega} \sim {\rm \omega} _{^h }$. The wavelength (λ = 2π/q) is inversely proportional to q, thus one can conclude that steep ripples at closer distances should be constructed for resonant excitation of THz radiation. The reason behind the requirement of smaller periodicity factor q (or larger ripple wavelength λ) for the excitation of high frequency THz waves can be traced in resonance condition
${\rm \omega} \sim {\rm \omega} _{^h }$. The wavelength (λ = 2π/q) is inversely proportional to q, thus one can conclude that steep ripples at closer distances should be constructed for resonant excitation of THz radiation. The reason behind the requirement of smaller periodicity factor q (or larger ripple wavelength λ) for the excitation of high frequency THz waves can be traced in resonance condition ![]() $\vec k = \vec k_1 - \vec k_2 + q$ and ω = ω1 − ω2. To increase ω, one has to increase ω1 by keeping ω2 fixed i.e., Δω = Δω1. Wave vectors
$\vec k = \vec k_1 - \vec k_2 + q$ and ω = ω1 − ω2. To increase ω, one has to increase ω1 by keeping ω2 fixed i.e., Δω = Δω1. Wave vectors ![]() $\vec k$ and
$\vec k$ and ![]() $\vec k_1$ change corresponding to changes in ω and ω1 respectively [keeping
$\vec k_1$ change corresponding to changes in ω and ω1 respectively [keeping ![]() $\vec k_2$ fixed]. Thus,
$\vec k_2$ fixed]. Thus, ![]() $\Delta \vec k = \Delta \vec k_1 + \Delta q$. We know that for x-mode electromagnetic wave we have
$\Delta \vec k = \Delta \vec k_1 + \Delta q$. We know that for x-mode electromagnetic wave we have
 $$\left. {\displaystyle{{d\vec k} \over {d{\rm \omega} }}} \right\vert _{{\rm high \ frequency}} \gt \left. {\displaystyle{{d\vec k} \over {d{\rm \omega} }}} \right\vert _{{\rm low \ frequency}}.$$
$$\left. {\displaystyle{{d\vec k} \over {d{\rm \omega} }}} \right\vert _{{\rm high \ frequency}} \gt \left. {\displaystyle{{d\vec k} \over {d{\rm \omega} }}} \right\vert _{{\rm low \ frequency}}.$$
Thus, for equal change in frequency, change in wave vector for high frequency x-wave will be greater than change in wave vector for low frequency x-mode wave. Since, beating laser (![]() ${\rm \omega} _1 \comma \; \vec k_1 $) and excited THz radiation (
${\rm \omega} _1 \comma \; \vec k_1 $) and excited THz radiation (![]() ${\rm \omega} \comma \; \vec k$) have same state of polarization (x-mode polarization). In the present scheme, thus for equal change in frequency
${\rm \omega} \comma \; \vec k$) have same state of polarization (x-mode polarization). In the present scheme, thus for equal change in frequency ![]() $\Delta {\rm \omega} = \Delta {\rm \omega} _1$ we have
$\Delta {\rm \omega} = \Delta {\rm \omega} _1$ we have ![]() $\Delta \vec k \lt \Delta \vec k_1$. So, we can conclude that periodicity factor q should be reduced (corresponding to
$\Delta \vec k \lt \Delta \vec k_1$. So, we can conclude that periodicity factor q should be reduced (corresponding to ![]() $\Delta \vec k = \Delta \vec k_1 + \Delta \vec q$) to enhance the frequency of excited THz radiation.
$\Delta \vec k = \Delta \vec k_1 + \Delta \vec q$) to enhance the frequency of excited THz radiation.

Fig. 2. Plot of the normalized ripple factor qc/ωp as a function of the normalized THz wave frequency ω/ωp and normalized cyclotron frequency ωc/ωp.
Figure 3a exhibits the variation of normalized THz wave amplitude (A y/0.15A) as a function of THz frequency (ν) and applied magnetic field B c. Two mountain ranges of high THz amplitude excitation are observed which are corresponding to two propagating frequency regimes of extra ordinary electromagnetic wave in plasma. These two frequency regime are given by (1) ωL < ω< ωh (Region II of Fig. 3b) and (2) ω > ωR (Region IV of Fig. 3b), where ![]() ${\rm \omega} _L = {1 / 2}\lsqb\! - {\rm \omega} _c + \sqrt {{\rm \omega} _c^2 + 4{\rm \omega} _p^2 } \rsqb $ and
${\rm \omega} _L = {1 / 2}\lsqb\! - {\rm \omega} _c + \sqrt {{\rm \omega} _c^2 + 4{\rm \omega} _p^2 } \rsqb $ and ![]() ${\rm \omega} _R =$
${\rm \omega} _R =$![]() ${1 / 2}\lsqb {\rm \omega} _c + \sqrt {{\rm \omega} _c^2 + 4{\rm \omega} _p^2 } \rsqb $. These two mountains are separated by a regime of frequency (Region III of Fig. 3b) in which ω2/k 2 becomes negative and propagation of wave stopped.
${1 / 2}\lsqb {\rm \omega} _c + \sqrt {{\rm \omega} _c^2 + 4{\rm \omega} _p^2 } \rsqb $. These two mountains are separated by a regime of frequency (Region III of Fig. 3b) in which ω2/k 2 becomes negative and propagation of wave stopped.

Fig. 3. (a) Sketch of the normalized THz amplitude (A y/0.15A) as a function of the THz frequency v(THz) and applied static magnetic field B c. Other normalized parameters are a 0 = 5, z = 1, y/a 0 = 0.05, v 1 = 0.3, n q0/n 0 = 0.3. (b) Sketch of the normalized THz frequency ω/ωp and cyclotron frequency ω/ωc.
Peaks of both amplitude mountains are corresponding to resonance conditions which occurs at ![]() ${\rm \omega}\,{\sim}\, {\rm \omega} _h $ and
${\rm \omega}\,{\sim}\, {\rm \omega} _h $ and ![]() $ {\rm \omega} \,{\sim}\, {\rm \omega} _R $, respectively. The frequency of THZ radiation having maximum amplitude shifts toward higher end of frequency as applied magnetic field increases due to enhanced value ωh and ωR. Similar type of observation can be drawn from Figure 4 in which normalized amplitude of THz radiation is plotted as a function of THz frequency and normalized distance travelled in z-direction. THz radiation of frequency 1 THz, (1.1 THz and 1.2 THz), (1.2 THz and 1.3 THz), and (1.3 THz and 1.5 THz) are achieved by applying dc magnetic field (B 0) 0, 107 kG, 178 kG, and 285kG, respectively. Thus maximum energy transfer from beating lasers to THz radiation takes place at resonance condition and frequency of THz can be tuned by changing applied magnetic field. As the amplitude of THz radiation enhances in z-direction thus amplitude of excited THz radiation can also be tuned by varying plasma length.
$ {\rm \omega} \,{\sim}\, {\rm \omega} _R $, respectively. The frequency of THZ radiation having maximum amplitude shifts toward higher end of frequency as applied magnetic field increases due to enhanced value ωh and ωR. Similar type of observation can be drawn from Figure 4 in which normalized amplitude of THz radiation is plotted as a function of THz frequency and normalized distance travelled in z-direction. THz radiation of frequency 1 THz, (1.1 THz and 1.2 THz), (1.2 THz and 1.3 THz), and (1.3 THz and 1.5 THz) are achieved by applying dc magnetic field (B 0) 0, 107 kG, 178 kG, and 285kG, respectively. Thus maximum energy transfer from beating lasers to THz radiation takes place at resonance condition and frequency of THz can be tuned by changing applied magnetic field. As the amplitude of THz radiation enhances in z-direction thus amplitude of excited THz radiation can also be tuned by varying plasma length.

Fig. 4. Plot of the normalized THz amplitude (A y/0.15A 0) as a function of the THz wave frequency v(THz) and normalized transverse distance z at different cyclotron frequency (a) ωc = 0.0, (b) ωc = 0.3, (c) ωc = 0.5, (d) ωc = 0.8. Other normalized parameters are y/a 0 = 0.05, v 1 = 0.3, n q0/n 0 = 0.3
It can be seen from Figure 5 that THz amplitude has maximum value on the axis (y/a 0 = 0) and decreases as one moves off axis which can be attributed to the maximum value of ponderomotive force on the axis. Thus, radiation emitted in the present scheme using x-mode triangular lasers is more colliminated as compared to other schemes (Xie et al., Reference Xie, Dai and Zhang2006). The amplitude of excited THz radiation is depending on the ponderomotive force exerting by the laser beams in the plasma (as shown in Eq. (15)). As laser beams propagating in z direction has transverse spatial dependency (triangular shaped) along y direction, the ponderomotive force will also have transverse dependency. Hence this behavior is appearing in our result showing the profile of THz radiation propagating in z direction and having transverse dependency. It can also be explained in another way: if we choose a particular value of y, and solve Eq. (15), we will have the variation of A y as a function of longitudinal direction z. Now if we choose another value of y, then we will again find different one-dimensional variation of A y because of different value of ponderomotive force (which is dependent on transverse direction y). Hence due to direct effect of laser profiles and ponderomotive force, excited THz radiation amplitude A y will also exhibit the transverse dependency.

Fig. 5. Plot of the normalized THz amplitude (A y/0.15A 0) as a function of the normalized transverse distancezand normalized beam width y/a 0. Other normalized parameters are v 1 = 0.3, ω1 = 12, n q0/n 0 = 0.3, ωc = 0.3, a 0 = 5, ω = 1.1.
Finally, we calculated the efficiency of the present scheme based on the energies of the lasers and emitted radiation. The average electromagnetic energy stored in unit volume in electric and magnetic fields (Malik et al. Reference Malik, Malik and Stroth2012; Reference Malik, Malik and Nishida2011) yields
 $$\eqalign{W_{THz} &= \displaystyle{{{\rm \varepsilon} _0 } \over {16{\rm \pi} }}\bigg[{\displaystyle{1 \over {4k}}\displaystyle{{n_{q0} } \over {n_0 }}\displaystyle{{{\rm \omega} {\rm \omega} _p^2 } \over {{\rm \omega} ^2 - {\rm \omega} _h^2 }}\displaystyle{z \over {ec^2 }}\bigg[{i\bigg({\displaystyle{{{\rm \omega} ^2 - {\rm \omega} _p^2 } \over {\rm \omega} } - \bigg\vert {\displaystyle{{{\rm \varepsilon} _{zy} } \over {{\rm \varepsilon} _{zz} }}} \bigg\vert {\rm \omega} _c } \bigg) }} F_{\!py} \cr & \quad + \bigg({{\rm \omega} _c - {\rm \omega} \bigg\vert {\displaystyle{{{\rm \varepsilon} _{zy} } \over {{\rm \varepsilon} _{zz} }}} \bigg\vert } \bigg)F_{\!pz} \bigg] \bigg]^2.}$$
$$\eqalign{W_{THz} &= \displaystyle{{{\rm \varepsilon} _0 } \over {16{\rm \pi} }}\bigg[{\displaystyle{1 \over {4k}}\displaystyle{{n_{q0} } \over {n_0 }}\displaystyle{{{\rm \omega} {\rm \omega} _p^2 } \over {{\rm \omega} ^2 - {\rm \omega} _h^2 }}\displaystyle{z \over {ec^2 }}\bigg[{i\bigg({\displaystyle{{{\rm \omega} ^2 - {\rm \omega} _p^2 } \over {\rm \omega} } - \bigg\vert {\displaystyle{{{\rm \varepsilon} _{zy} } \over {{\rm \varepsilon} _{zz} }}} \bigg\vert {\rm \omega} _c } \bigg) }} F_{\!py} \cr & \quad + \bigg({{\rm \omega} _c - {\rm \omega} \bigg\vert {\displaystyle{{{\rm \varepsilon} _{zy} } \over {{\rm \varepsilon} _{zz} }}} \bigg\vert } \bigg)F_{\!pz} \bigg] \bigg]^2.}$$Here W pump is the average energy density of the pump lasers of triangular shape. The ratio of THz energy to pump energy gives the efficiency η as below
 $${\rm \eta} = \displaystyle{{W_{THz} } \over {W_{\!pump} }} = \left\vert {\displaystyle{{A_y } \over {A_0 }}} \right\vert ^2\comma \;$$
$${\rm \eta} = \displaystyle{{W_{THz} } \over {W_{\!pump} }} = \left\vert {\displaystyle{{A_y } \over {A_0 }}} \right\vert ^2\comma \;$$ $$\eqalign{{\rm \eta} &= \Bigg[{\displaystyle{1 \over {4k}}\displaystyle{{n_{q0} } \over {n_0 }}\displaystyle{{{\rm \omega} {\rm \omega} _p^2 } \over {{\rm \omega} ^2 - {\rm \omega} _h^2 }}\displaystyle{z \over {ec^2 }}\bigg[{i\bigg({\displaystyle{{{\rm \omega} ^2 - {\rm \omega} _p^2 } \over {\rm \omega} } - \bigg\vert {\displaystyle{{{\rm \varepsilon} _{zy} } \over {{\rm \varepsilon} _{zz} }}} \bigg\vert {\rm \omega} _c } \bigg)}} F_{\!py} \cr & \quad + \bigg({{\rm \omega} _c - {\rm \omega} \bigg\vert {\displaystyle{{{\rm \varepsilon} _{zy} } \over {{\rm \varepsilon} _{zz} }}} \bigg\vert } \bigg)F_{\!pz} \bigg] \Bigg]^2.}$$
$$\eqalign{{\rm \eta} &= \Bigg[{\displaystyle{1 \over {4k}}\displaystyle{{n_{q0} } \over {n_0 }}\displaystyle{{{\rm \omega} {\rm \omega} _p^2 } \over {{\rm \omega} ^2 - {\rm \omega} _h^2 }}\displaystyle{z \over {ec^2 }}\bigg[{i\bigg({\displaystyle{{{\rm \omega} ^2 - {\rm \omega} _p^2 } \over {\rm \omega} } - \bigg\vert {\displaystyle{{{\rm \varepsilon} _{zy} } \over {{\rm \varepsilon} _{zz} }}} \bigg\vert {\rm \omega} _c } \bigg)}} F_{\!py} \cr & \quad + \bigg({{\rm \omega} _c - {\rm \omega} \bigg\vert {\displaystyle{{{\rm \varepsilon} _{zy} } \over {{\rm \varepsilon} _{zz} }}} \bigg\vert } \bigg)F_{\!pz} \bigg] \Bigg]^2.}$$ The efficiency of present scheme is proportional to the square of ripple amplitude, which can be explained on the basis of more charge carriers involved in excitation of nonlinear current responsible for the generation of THz radiation. The efficiency is also proportional to z 2 which can be explained as follows: as beating lasers propagate in z-direction, they encounter more and more periodic density ripples; higher the number of encountered periodic density ripples better will be the efficacy of three wave coupling required for THz radiation generation due to efficient momentum transfer (from ripple periodicity to nonlinear current ![]() $\vec J_{NL} $ to overcome the mismatch in momentum). At the same time, larger number of electrons due to higher number of density ripples will produce larger nonlinear current. The efficiency of THz radiation generation is plotted as a function of THz frequency and applied magnetic field in Figure 6. In the present scheme, the efficiency of THz radiation generation about 2.5% can be achieved for the frequency range 1–1.3 THz by applying magnetic field about 100 kG. It can be noticed that the efficiency of the present scheme is much better than reported by other investigators. For example, Malik et al. (Reference Malik, Malik and Nishida2011) have reported the conversion efficiency about 0.002 by beating of two spatial-Gaussian lasers; Varshney et al. (Reference Varshney, Sajal, Singh, Kumar and Sharma2013) have reported the conversion efficiency about 10−3 by beating of two planer x-mode laser; conversion efficiency about 0.006 is achieved by Malik and Malik (Reference Malik and Malik2012) by using super Gaussian lasers; whereas present scheme achieved the conversion efficiency about 0.02 by using two triangular shaped x-mode lasers. Hamester et al. (Reference Hamster, Sullivan, Gordon, White and Falcone1993; Reference Hamster, Sullivan, Gordon and Falcone1994) also obtained the efficiency about 10−5 with a single laser that is Gaussian in space and time which is two order lesser as compared to the conversion efficiency of present scheme. Wu et al. (Reference Wu, Sheng and Zhang2008) reported theoretical as well as numerical simulation of powerful THz emission using inhomogeneous plasma density. In their model, the maximum energy conversion efficiency at peak intensity 5.48 × 1012 W/cm2 is 0.0005, which is much lower than present model. Kim et al. (Reference Kim, Taylor, Glownia and Rodriguez2008) proposed a model for the generation of THz radiation by irradiating different gases with a symmetry-broken laser field composed of the fundamental and second harmonic laser pulses. In that model, the energy conversion efficiency was about 10−5, which is three orders lesser as compared to present model.
$\vec J_{NL} $ to overcome the mismatch in momentum). At the same time, larger number of electrons due to higher number of density ripples will produce larger nonlinear current. The efficiency of THz radiation generation is plotted as a function of THz frequency and applied magnetic field in Figure 6. In the present scheme, the efficiency of THz radiation generation about 2.5% can be achieved for the frequency range 1–1.3 THz by applying magnetic field about 100 kG. It can be noticed that the efficiency of the present scheme is much better than reported by other investigators. For example, Malik et al. (Reference Malik, Malik and Nishida2011) have reported the conversion efficiency about 0.002 by beating of two spatial-Gaussian lasers; Varshney et al. (Reference Varshney, Sajal, Singh, Kumar and Sharma2013) have reported the conversion efficiency about 10−3 by beating of two planer x-mode laser; conversion efficiency about 0.006 is achieved by Malik and Malik (Reference Malik and Malik2012) by using super Gaussian lasers; whereas present scheme achieved the conversion efficiency about 0.02 by using two triangular shaped x-mode lasers. Hamester et al. (Reference Hamster, Sullivan, Gordon, White and Falcone1993; Reference Hamster, Sullivan, Gordon and Falcone1994) also obtained the efficiency about 10−5 with a single laser that is Gaussian in space and time which is two order lesser as compared to the conversion efficiency of present scheme. Wu et al. (Reference Wu, Sheng and Zhang2008) reported theoretical as well as numerical simulation of powerful THz emission using inhomogeneous plasma density. In their model, the maximum energy conversion efficiency at peak intensity 5.48 × 1012 W/cm2 is 0.0005, which is much lower than present model. Kim et al. (Reference Kim, Taylor, Glownia and Rodriguez2008) proposed a model for the generation of THz radiation by irradiating different gases with a symmetry-broken laser field composed of the fundamental and second harmonic laser pulses. In that model, the energy conversion efficiency was about 10−5, which is three orders lesser as compared to present model.

Fig. 6. Variation of efficiency of THz radiation η as a function of the THz frequency v(THz) and applied static magnetic field B c. Other normalized parameters are v 1 = 0.3, ω1 = 12, n q0/n 0 = 0.3, ωc = 0.3, a 0 = 5, z = 1, y/a 0 = 0.5.
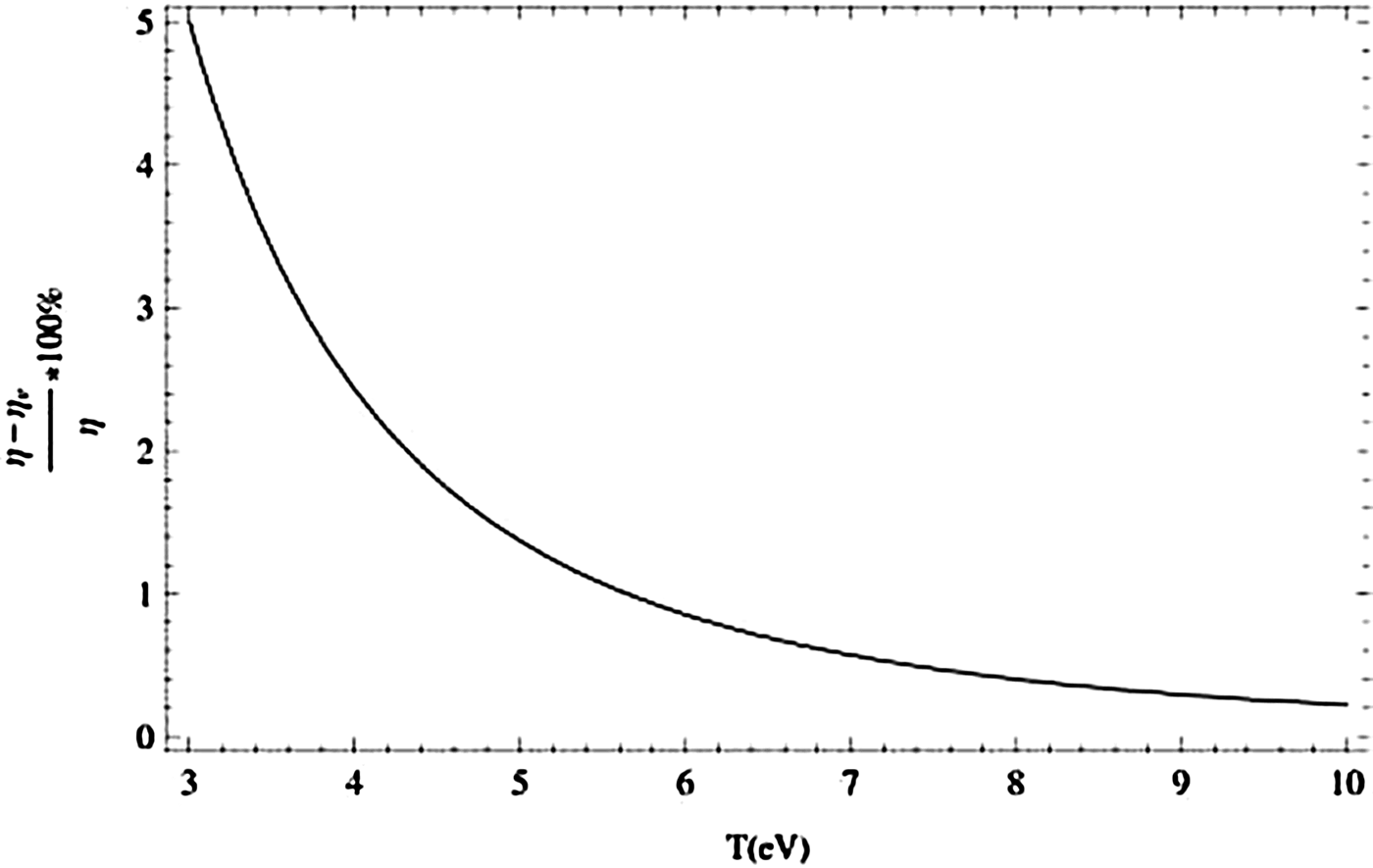
Effect of electron collision frequency (ν) on the efficiency of present scheme as a function of electron temperature is shown in Figure 7. Electron collision frequency depends upon electron temperature by the expression given by ν = (zωp/10N D) ln(9N D/z), where N D = 4πn 0λDe3/3, λDe is the electron Debye length and n 0 is the electron density in plasmas. As plasma electron temperature increases, electron collision frequency (ν) decreases; as a result of which percentage change in efficiency [{(η − ην)/η} × 100] of the present THz generation scheme decreases. Here, ην and η are the efficiencies of the scheme with and without electron collisions respectively. All the dimensionless parameters are chosen for CO2 laser (λ = 1.06 × 10−5 m) having frequency ω1 = 2 × 1014 rad/s and intensity I L = 2 × 1015 wcm−2.

Fig. 7. Percentage change in efficiency of THz radiation generation as a function of plasma temperature T (eV).
4. CONCLUSIONS
Dynamics of THz radiation generation by beating of two x-mode laser beams in rippled magnetized plasma is studied, when only ponderomotive nonlinearity is operative. Triangular envelop of x-mode laser beams is utilized to enhance beat ponderomotive force acting on plasma electrons. The extra momentum required to excite THz wave resonantly by beating of two x-mode lasers of frequencies in upper hybrid range is provided by the periodicity of density ripples. The required ripple wave number depends upon THz frequency and applied magnetic field. It decreases as the THz frequency increases and increases as the magnetic field increases. Thus, frequency of THz radiation can be easily tuned by varying plasma density and applied magnetic field. The nonlinear mechanism which generates the THz radiation can be understood as follows: the nonlinear interaction of laser beams with the plasma having static magnetic field generates the velocity perturbation which leads to density perturbation. Static magnetic field imparts extra longitudinal component to oscillatory velocity of plasma electrons resulting in to transverse ponderomotive force. Both the components of ponderomotive force (Eq. (3) and Eq. (4)) are responsible for density perturbation. As a result, a nonlinear current at beat wave frequency is generated due to coupling between density ripples and velocity components of electron as shown in Eq. (11). Since the difference in laser beam frequencies is in the range of THz and phase matching conditions are satisfied, the nonlinear current generated at beat frequency generates the desired THz wave. The THz amplitude can be controlled by laser plasma parameters and magnitude of applied static magnetic field as shown in Eq. (16). In this scheme, magnetic field plays two roles (1) it controls the phase velocity and group velocity of beating lasers and (2) the polarization of generated THz wave (Sharma et al., Reference Sharma, Monika, Sharma, Chauhan and Jia2010). The THz amplitude scales directly to the amplitude of density ripples and maximizes as frequency (ω) approaches to resonance frequency (≈ωh). THz radiation emitted by beating of two triangular shaped lasers is more colliminated (Fig. 5) as compared to plane lasers and Gaussian shaped lasers (Malik et al., Reference Malik, Malik and Stroth2012). In conclusion, we can say that the efficiency, amplitude and tunability of the present THz generation scheme is better than others.