1. INTRODUCTION
When the field of nuclear physics was created by Lord Rutherford just after 1900, it was evident from the beginning that the energy exchanges for nuclear processes are about 10 million times higher than those in chemical reactions. The binding energy of the protons and neutrons in a nucleus is of the order of 10 million electron volts (MeV) while the typical chemical reaction binding energies are of about 1 electron volt (eV) only. Using Rutherford's experiments with Albert Einstein's explanation of the connection between mass and energy, as demonstrated by the most famous equation in physics E = mc 2 (c is speed of light and E is the energy contained in mass m), it was evident that the burning in nuclear reactions is related to 10 million times more energy than in chemical reactions.
There are two types of nuclear reactions that can yield energy: Fission and fusion. During the fission process, a heavy element like uranium (element number Z = 92) splits into two elements and neutron emission while during the fusion two light elements are to be combined into a heavier one. The nuclear fusion of the light elements, from the one proton hydrogen (Z = 1) up to iron (Z = 26) can release energies of the order of few MeV per reaction. The most important nuclear fusion, namely the one that gives life to our planet, is the hydrogen cycle producing the helium nuclei (α) and yielding the energy of the sun. This cycle includes the weak interaction of proton–proton fusion creating a deuterium that further collides with a proton to get the helium-3 isotope that fuses with another helium-3 to get the final alpha nuclei.
The proton–proton fusion cross section has by far the lowest cross section of this chain of reactions and it is given by σ(p + p → D + e+ + νe) = [S(E)/E]exp[−2πη(E)], where e+ is the positron and νe denotes the neutrino (Eliezer & Ross, Reference Eliezer and Ross1974) of the electron class. [S(E)/E] = 4.0 × 10−46 keV.cm2/E keV and η(E) = 2πe2/(hv) where v is the relative velocity between the two colliding protons. The rate and timetable of this cycle are dominated by the H–H interaction of the nuclei of the light hydrogen H, the protons.
The fusion power (in watts) is in general given for the interaction of particle 1 with particle 2 by
The energy power in watts P[W] is proportional to the number densities n 1 and n 2 times the rate 〈σv〉, where σ is the cross section for fusion and v is the relative velocity between the two fusing particles, times the volume V where the fusion reactions take place, times the average energy released (in Joules) by the fusion reactions E[J]. For our sun the hydrogen–hydrogen rate of fusion is of the order of 〈σv〉 = 10−43 cm3/s, an extremely small value. The fusion is possible because the sun is extremely big.
In order to achieve fusion on our planet in a controllable way, one has to reduce the volume by many orders of magnitude and this is possible because we look for strong interaction fusion with a rate 〈σv〉 of about 10−15 cm3/s, namely many orders of magnitude larger. For this purpose, in the context of energy production on our planet, the fusion (1) of the heavy hydrogen isotopes deuterium (D) and tritium (T) and (2) the hydrogen H (proton) reaction with the boron isotope 11 (B11) are of great interest
Using equation (1) for a terrestrial power plant of P = 1 gigawatt (GW), with an energy output per reaction of about 10 MeV with the maximum reaction rates of 〈σv〉 = 10−15 cm3/s, we need n 1 n 2 V equal about 1036 cm−3. There are two distinct possibilities to achieve this limit: (a) A continuous operation with magnetic confinement of dilute plasmas, with the density order of n = 1013 cm−3 and large volumes V = 1010 cm3 with the confinement of the reacting plasmas by magnetic fields (Bigot, Reference Bigot2017) and – alternatively – (b) Inertial confinement of (a tiny “small sun”) compressed solid-state plasma with densities number of 1023 cm−3 and larger for pulsating operation.
The discovery of the laser paved the way from the beginning to use it for miniaturization of the ignition for a controlled pulsating fusion energy generation in a controlled way in power reactors (Sakharov, Reference Sakharov1960; Basov & Krokhin et al. Reference Basov, Krokhin, Grivet and Bloembergen1964; Dawson, Reference Dawson1964; Hora, Reference Hora1964; Nuckolls, Contributions to the Genesis and Progress of UCF, Reference Nuckolls2007). The following developments at the National Ignition Facility NIF in Livermore/California with the largest laser in the world arrived at fusion energy gains rather close to but not yet the desired ignition point (Hora, Reference Hora2013; Hurricane et al., Reference Hurricane, Callahan, Casey, Celliers, Cerjan, Dewald, Dittrich, Döppner, Hinkel, Berzak Hopkins, Kline, Le Pape, Ma, Macphee, Milovich, Pak, Park, Patel, Remington, Salmonson, Springer and Tommasini2014; Hinkel et al., Reference Hinkel, Berzak-Hopkins, Jones, Callahan and Hurricane2016).
For a thermal equilibrium plasma, the DT was the first choice of a fusion reactor because it reaches the high value of 〈σv〉 of 10−15 cm3/s for the lowest possible temperature (at T = 20 keV). In contrast to the DT reaction, the boron reaction HB11 reaction is very much less efficient under conditions of thermal equilibrium. The values of 〈σv〉 for the clean HB11 fusion is so much lower that the gain is smaller by five orders of magnitude, a factor of 100,000 such this option of fusion was usually excluded. This reaction reaches the large 〈σv〉 for temperatures at temperatures of about 600 keV and for laser ignition a compression to 100,000 times solid-state density was considered as extremely difficult to be achieved using the conventional theories (see Section 9.6 of Hora, Reference Hora2016).
The HB11 reaction was of special interest because no neutrons (n) were produced when the reacting H-nuclei (protons) had lower energy than about 3 MeV. HB11 is then an environmentally clean reaction in contrast to DT (Tahir & Hoffmann, Reference Tahir and Hoffmann1997). The aim of the neutron-free clean boron fusion was nevertheless highly attractive, that several proposals were developed by highly qualified experts (Meglich & Morwood et al., Reference Meglich and Morwood1988). The only way out was to work at conditions without local thermal equilibrium, LTE, and using nonlinearities as concluded from preceding research (Hora, Reference Hora1988). A further advantage of the HB11 reaction was the generation of three helium nuclei (alpha particles), Eq. (2b), which can be expected for producing an avalanche multiplication.
For fusion at conditions of non-thermal ignition, the laser was the ideal tool when using the result (Hora et al., Reference Hora, Lalousis and Moustaizis2014, Reference Hora, Korn, Giuffrida, Marganoone, Picciotto, Krasa, Jungwirth, Ullschmied, Lalouais, Eliezer, Miley, Moustaizis and Mourou 2015a , Reference Hora, Lalousis, Giuffrida, Margarone, Korn, Eliezer, MILEYi, Moustaizis and Mourou b ) that the electric and magnetic fields E and H of a sufficiently intense laser beam cause an acceleration of nearly solid density plasma blocks without heating within a picosecond (ps) interaction to velocities above 109 cm/s (Lawrence, Reference Lawrence1978; see Figures 10.18a & b of Hora, Reference Hora1988). This numerical result of 1978 was exactly reproduced in agreement with the measurements by Sauerbrey (Reference Sauerbrey1996) with laser pulses of picoseconds duration and powers between Terawatt (TW) and petawatt (PW) available 1996 and repeated by Földes et al. (Reference Földes, Bakos, Gal, Juhasz, Kedves, Koscis, Szatmari and Veres2000).
This non-thermal ignition of solid density fusion fuel was the result by Chu (Reference Chu1972) and by Bobin (Reference Bobin, Schwarz and Hora1974) by initiation of the reaction to be produced within a picosecond, when hydrodynamic computations included – next to thermal properties – the interaction of the laser fields resulting in nonlinear (ponderomotive) forces dominating the generation of the plasma blocks (Hora, Reference Hora1981, Reference Hora2016). An updating of the hydrodynamic computations (Hora et al., Reference Hora, Malekynia, Ghoranneviss, Miley and He2008; Lalousis et al., Reference Lalousis, Hora, Eliezer, Martinez-Val, Moustaizis, Miley and Mourou2013) and subsequently in full agreement with using a more detailed genuine multi-fluid code reproduced these measurements of ultrahigh acceleration for DT-fusion (Sauerbrey, Reference Sauerbrey1996; Földes et al., Reference Földes, Bakos, Gal, Juhasz, Kedves, Koscis, Szatmari and Veres2000). Furthermore, it was then a great surprise, when applying this for HB11 fusion (Hora, Reference Hora2009; Hora et al., Reference Hora, Miley, Azizi, Malekynia, Ghoranneviss and He2009, Reference Hora, Miley, Ghorannviss, Malekynia, Azizi and He2010), that the ignition threshold for HB11 was elevated by five orders of magnitudes above the classical values arriving at the level of DT due to the non-thermal transfer of the laser energy directly into the ultrahigh acceleration of the plasma blocks.
Another advantage was the very first measurement of HB11 fusion (Belyaev et al., Reference Belyaev, Matafonov, Vinogradov, Krainov, Lisitsa, Roussetski, Ignatyev and Andrianov2005) by using lasers with thousand reactions per laser shot, followed by more than 1 million reactions (Labaune et al., Reference Labaune, Deprierraux, Goyon, Loisel, Yahia and Rafelski2013) and then by one billion reactions (Picciotto et al., Reference Picciotto, Margarone, Velyhan, Bellini, Krasa, Szydlowski, Bertuccio, Shi, Margarone, Prokupek, Malinowska, Krouski, Ullschmied, Laska, Kucharik and Korn2014). Comparison with DT fusion confirmed that this could be achieved only by avalanche reactions (Hora, Reference Hora2014; Hora et al., Reference Hora, Korn, Giuffrida, Marganoone, Picciotto, Krasa, Jungwirth, Ullschmied, Lalouais, Eliezer, Miley, Moustaizis and Mourou2015). The detailed evaluation of these measurements (Margarone et al., Reference Margarone, Picciotto, Velyhan, Krasa, Kucharik, Mangione, Szydlowsky, Malinowska, Bertuccio, Shi, Crivellari, Ullschmied, Bellutti and Korn2015) based on elastic nuclear collisions towards the exceptionally high HB11 reaction around 600 keV (Eliezer et al., Reference Eliezer, Hora, Korn, Nissim and Martinez-Val2016; Hora et al., Reference Hora, Eliezer, Nissim, Xu and Lalousis2017b ) showed an increase of the gains by further four orders of magnitudes.
Based on these nine orders of magnitudes higher reactivity of HB11 at non-local thermodynamic equilibrium (LTE) conditions, a fusion power reactor was designed (Hora et al., Reference Hora, Lalousis and Moustaizis2014; Lalousis et al., Reference Lalousis, Hora and Moustaizis2014; Hora, Reference Hora2015) with picosecond laser pulses of more than 30 Petawatt power that are expected to ignite 14 milligram hydrogen-boron for producing 300 kWh energy.
The following sections describe properties for aiming environmentally clean, low cost, and sustainable energy production, and a list of research topics. Single laser beam ignition for fusion energy is an innovation for alternative conditions differing from the usual spherical irradiation by many synchronized laser beams. These developments were initiated in 2014 (Hora et al., Reference Hora, Lalousis and Moustaizis2014, Reference Hora, Korn, Giuffrida, Marganoone, Picciotto, Krasa, Jungwirth, Ullschmied, Lalouais, Eliezer, Miley, Moustaizis and Mourou 2015a ; Lalousis et al., Reference Lalousis, Hora and Moustaizis2014) following the Patent Cooperation Treaty international patent with the priority of 23 March 2014 (Hora & Kirchoff, Reference Hora and Kirchoff2017) for the now progressing national phases (Hora et al., Reference Hora, Eliezer, Nissim, Xu and Lalousis 2017a ). These developments (Hora et al., Reference Hora, Korn, Giuffrida, Marganoone, Picciotto, Krasa, Jungwirth, Ullschmied, Lalouais, Eliezer, Miley, Moustaizis and Mourou2015; Hora & Kirchhoff, Reference Hora and Kirchhoff2015a ) followed step by step (Hora et al. Reference Hora, Eliezer, Nissim, Xu and Lalousis2017b , Reference Hora, Eiezer, Wang, Korn, Nissim, Xu, Lalousis, Kirchhoff and Miley c ) for the first realistic option of an environmentally absolute clean reactor for the fusion of hydrogen with the boron isotope 11 (HB11) for low cost and sustainable large-scale energy generation.
HB11 fusion (Oliphant & Rutherford, Reference Oliphant and Rutherford1933) is well known to avoid generation of neutrons that in all other cases of nuclear energy reactors are producing dangerous radioactive waste. The energy of the reacting hydrogen nuclei, the protons, have to have energies below MeV for a reaction completely free from neutrons.
The disadvantage of HB11 fusion is that it is about five orders of magnitudes – 100,000 times – more difficult and was considered as impossible (see Chapter 9.6 of Hora, Reference Hora2016) compared with the easiest fusion of heavy with superheavy hydrogen, deuterium and tritium at conditions of LTE of the reacting plasma. And even DT fusion is still only close below breakeven despite enormous research using magnetic confinement (MCF) (Bigot, Reference Bigot2017) or inertial confinement (ICF) (Hora, Reference Hora2013) fusion.
Against these facts of the impossibility of HB11, the aneutronic aspect attracted prominent experts to search for solutions (Hora et al., Reference Hora, Eliezer, Kirchhoff, Korn, Lalaousis, Miley and Moustaizis2017a ). This in principle could only be based on conditions without thermal equilibrium (Hora, Reference Hora1988; Hora et al., Reference Hora, Lalousis, Moustaizis, Földes, Miley, Yang, He, Eliezer and Martinez-Val2012) and without using nonlinear effects (see clarifications by Feynman, Section 6.3 of Hora, Reference Hora2016). An example of studies of plasmas different from LTE thermal equilibrium plasmas was developed for the dusty plasmas (Fortov & Iakubov, Reference Fortov and Iakubov1998) with similar problems to the HB11 fusion (Hoffmann et al., Reference Hoffmann, Hora, Eliezer, Nissim, Fortov, Lalousis, Korn, Moustaizis, Kirchhoff and Martinez-Val2017) or non-neutral plasmas (Davidson, Reference Davidson2016). Attempts are using low-density plasma (Hirsch, Reference Hirsch1972; Rostoker et al., Reference Rostoker, Binderbauer and Monkhorst1997; Miley & Murali, Reference Miley and Murali2015) where however no fusion reactions were measured jet (Hora et al., Reference Hora, Eliezer, Kirchhoff, Korn, Lalaousis, Miley and Moustaizis2017a ). Following the principle (Hora, Reference Hora1988; Hora et al., Reference Hora, Badziak, Boody, Höpfl, Jungwirth, Kralikowa, Kraska, Laska, Parys, Perina, Pfeifer, Rohlena, Skala, Ullschmied, Wolowski and Woryna2002) to use a non-thermal ignition of HB11 fusion by laser pulses led to measured high gain HB11 reactions (Hora et al., Reference Hora, Korn, Giuffrida, Marganoone, Picciotto, Krasa, Jungwirth, Ullschmied, Lalouais, Eliezer, Miley, Moustaizis and Mourou2015) opening the option that ultra-highly accelerated plasma blocks with conversion of laser energy directly into directed plasma block motion in the range of solid-state densities, the present achievement is a nine orders higher gain of fusion energy than classical measured (Eliezer et al., Reference Eliezer, Hora, Korn, Nissim and Martinez-Val2016). This is even higher than DT (Hora et al., Reference Hora2015). The reason is the non-thermal ignition and the avalanche multiplication (Hora et al., Reference Hora, Lalousis and Moustaizis2014) of the generated three helium nuclei of reaction in agreement with the theory (Eliezer et al. Reference Eliezer, Hora, Korn, Nissim and Martinez-Val2016) for the experiments (Picciotto et al., Reference Picciotto, Margarone, Velyhan, Bellini, Krasa, Szydlowski, Bertuccio, Shi, Margarone, Prokupek, Malinowska, Krouski, Ullschmied, Laska, Kucharik and Korn2014; Margarone et al., Reference Margarone, Picciotto, Velyhan, Krasa, Kucharik, Mangione, Szydlowsky, Malinowska, Bertuccio, Shi, Crivellari, Ullschmied, Bellutti and Korn2015).
2. LASER BORON FUSION REACTOR WITH BASICALLY NEW PROPERTIES
Experiments for laser-driven DT fusion were based on spherical irradiation of laser beams. The laser amplifiers of the NIF experiment cover most of the size of three football fields for the experiment where the beams are collected by a 10 m diameter sphere (Fig. 1) to be focused into the center. The techniques of correct guiding, focusing and temporal scheduling of 196 laser beams were developed.

Fig. 1. Sphere of 10 m diameter at the NIF laser at the Lawrence Livermore National Laboratory LLNL in California where Laser beams are irradiated into the holes to and focused to diameters of about 100 micrometer diameter into holes of a capsule for indirect drive DT fusion in a sphere with a diameter above one millimeter producing the highest nuclear fusion gains (Hurricane et al., Reference Hurricane, Callahan, Casey, Celliers, Cerjan, Dewald, Dittrich, Döppner, Hinkel, Berzak Hopkins, Kline, Le Pape, Ma, Macphee, Milovich, Pak, Park, Patel, Remington, Salmonson, Springer and Tommasini2014; Hinkel et al., Reference Hinkel, Berzak-Hopkins, Jones, Callahan and Hurricane2016).
For the laser boron fusion, the reactor is of spherical shape, Figure 2, but with the basic simplification that the ignition of the reaction is produced only by one laser beam. The wall of the reactor sphere of at least 1 m radius for sustaining the generated helium nuclei (alpha particles of 2.9 MeV energy) of 300 kWh energy per shot has to be of steel or similar material of at least view millimeter thickness. The shock produced by the fusion reaction corresponds to that of a chemical explosive of about 50 g (Hora et al., Reference Hora, Korn, Giuffrida, Marganoone, Picciotto, Krasa, Jungwirth, Ullschmied, Lalouais, Eliezer, Miley, Moustaizis and Mourou2015). This comparably low shock compared with chemical reactions is due to the fact that this depends on the energy of the generated particles. This is given by the square root of the ratio between nuclear and chemical energy, reducing the nuclear explosion shock by a factor of few thousands against the chemical explosion apart from a softening to the shock front of the alphas.
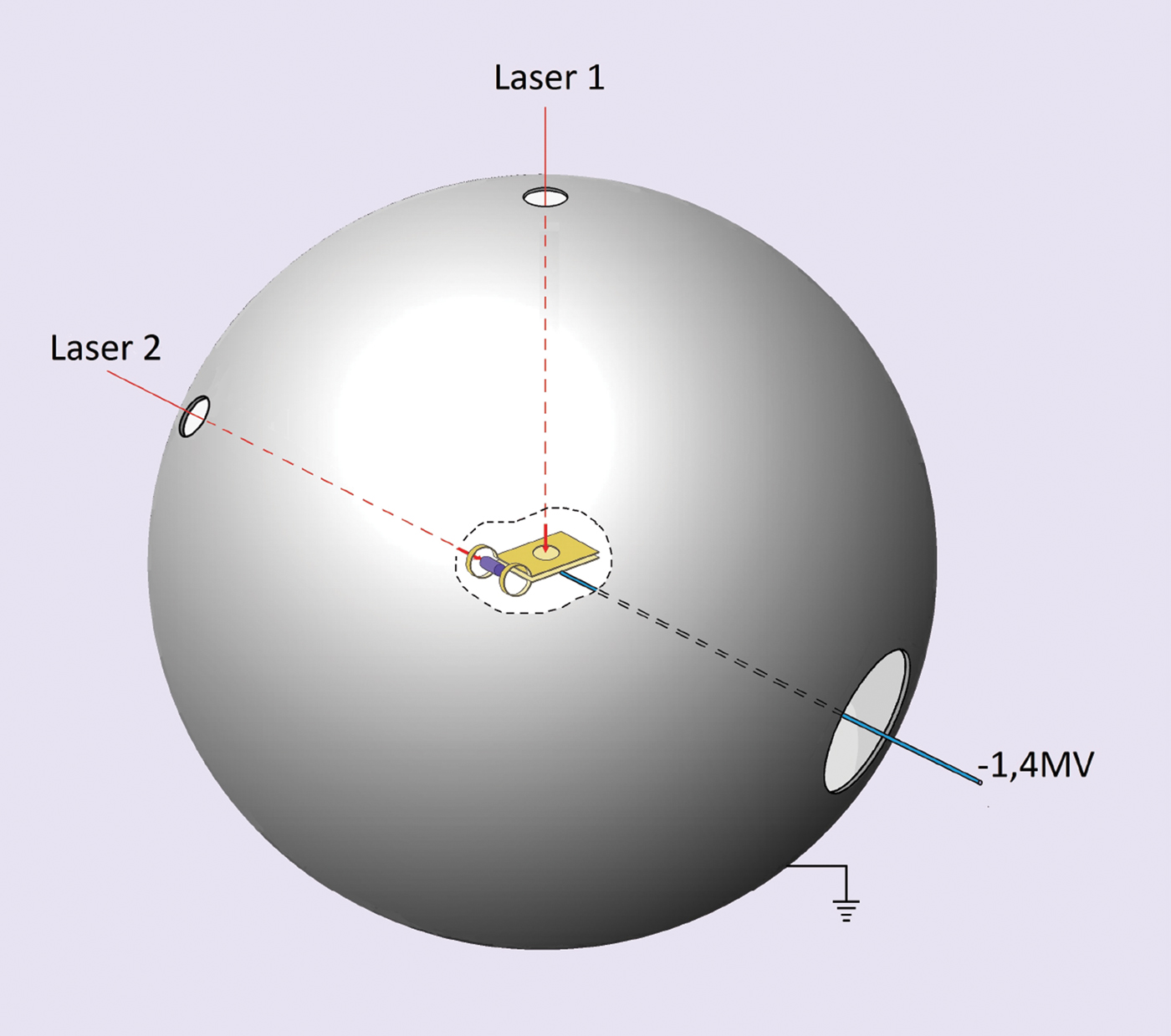
Fig. 2. Scheme of an economic electric power reactor for production of boron-fusion, absolutely free from the problem of dangerous nuclear radiation (Hora et al., Reference Hora2014, Reference Hora, Korn, Giuffrida, Marganoone, Picciotto, Krasa, Jungwirth, Ullschmied, Lalouais, Eliezer, Miley, Moustaizis and Mourou2015a , Reference Hora, Lalousis, Giuffrida, Margarone, Korn, Eliezer, MILEYi, Moustaizis and Mourou b ) with the estimated possibility of a power station producing electricity of up to a profit of $300 million/year (Hora, Reference Hora2015; Hora et al., Reference Hora, Eliezer, Nissim, Xu and Lalousis2017b ). Description of central reaction unit, see Figure 3.
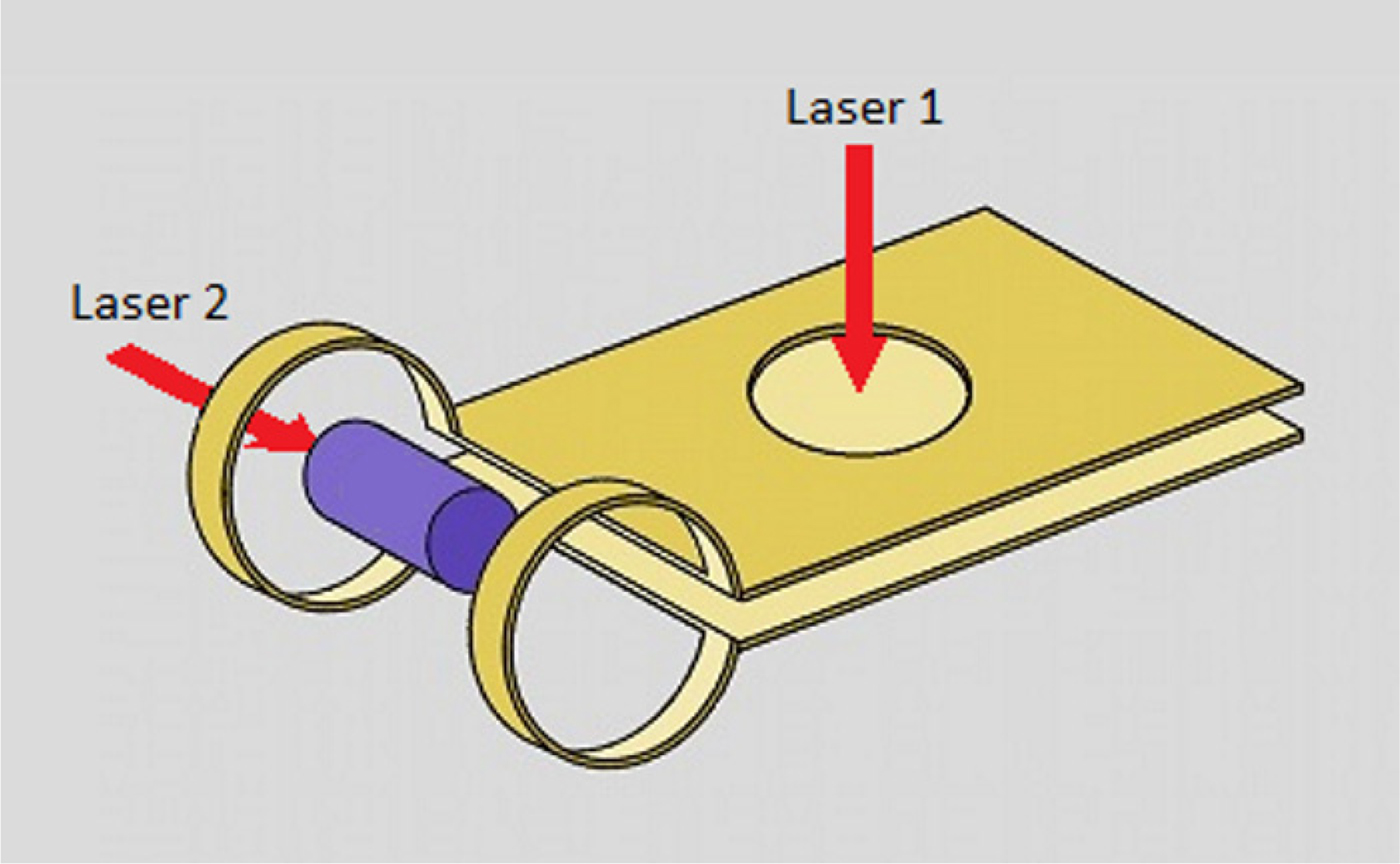
Fig. 3. Reaction unit in the center of the reactor of Figure 2 using “capacitor coil fields” (Fujioka et al., Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi2013). The cylindrical target with the HB11 fuel is co-axially located in a coil where during a ns a 4.5 kilotesla magnetic field is produced by a kJ–ns pulse of laser 1 (Fujioka et al. Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi2013; Santos et al., Reference Santos, Bailly-Gandvoux, Giuffrida, Forestercolleoni, Fuijoka, Zang, Korneev, Boullaud, Dor And, Batani, Chervrrot, Cross, Crowston, Dubois, Gazave, Greofri, D'humieres, Hulin, Ishihara, Kojima, Loyez, Marques, Nicolai, Peyrusse, Poye, Raffestin, Ribolzi, Roth, Schaumann, Serred, Tikhonchuk, Vacar and Woolsley2015; Tikhonchuk et al., Reference Tikhonchuk, Baylly-Grandvaux, Santos and Poye2017) for trapping the fuel plasmas. A ps-30 kJ laser pulse 2 initiates the non-thermal ignition of the fusion in the fuel (Hora, Reference Hora1988; Hora et al., Reference Hora, Korn, Giuffrida, Marganoone, Picciotto, Krasa, Jungwirth, Ullschmied, Lalouais, Eliezer, Miley, Moustaizis and Mourou2015, Reference Hora, Eiezer, Wang, Korn, Nissim, Xu, Lalousis, Kirchhoff and Miley2017c ).
The basic difference to the reaction unit in the center of the sphere is that this is not for a spherical irradiation but for a cylindrical geometry of the fusion fuel Figure 3 about which details are to be discussed in the following section. If the unit is at the same potential as the sphere, the energy of the alphas is absorbed in the wall sphere and has then to be converted thermally for use in electric generators.
Another advantage is that nuclear energy of the mono-energetic alphas can be changed directly into electricity with a minimum of thermal losses into cooling systems if the unit is charged on a negative potential of less than but close to 1.4 V. The alphas are then slowed down when flying against the positive wall potential and the electrostatic gained energy can then directly converted into three-phase electric currents by techniques well developed by the HVDC high-voltage direct current transmission lines (Kanngiesser et al., Reference Kanngiesser, Huang and Lips1994; Hammons et al., Reference Hammons, Victor, Lesale, Uecker, Hausler, Retzmann, Staschus and Lang2012). This direct conversion of nuclear energy into electricity is indeed possible only if plasma discharge losses between the unit equipped with Faraday screening and the reactor wall can be sufficiently reduced, otherwise, the energy conversion of the alphas is possible only by the heating of the wall material.
What else is standard level for use in the HB11-reactor of Figure 2? Lasers for pulses up to picosecond duration and more than 30 PW power are well expectable within few years. In 2017, lasers with 0.17 ps, 10 PW power and one shot per minute are in use following Todd Ditmire (Reference Ditmire2017) and upgrading to the other specifications with one shot per second should be developed within the range of present-day technology, driven also for other most important applications than for laser boron fusion. The optical technology for guiding the 30 PW–ps of high contrast and modest focusing is on a much higher level developed for the case of NIF (Fig. 1) can be taken over, well appreciated that the achieved level at NIF is on a breathtaking high level.
The physics of the generation of the ultrahigh magnetic fields in the coils (Fujioka et al., Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi2013) is indeed an outstanding achievement following the work of Daido et al. (Reference Daido, Miki, Mima, Fujita, Sawaki, Fujita, Kitagawa, Nakai and Yamanaka1986) and of Hohenberger et al. (Reference Hohenberger, Chang, Fiksel, Knauer, Betti, Marshall, Meyerhofer, Séguin and Petrasso2012) using nanosecond laser pulses of usual level. Nevertheless, the studying of the field properties, the time dependence, and further improvement are of technology for laboratory projects on usual level.
The mechanically guiding of the reaction unit to the rector center is indeed not an easy topic but should be less difficult than the similar problems in the technology of micro-electronics and may be taken over from there. The technology for repeating the positioning of the unit into the reactor center for one event per second were following solutions based on technologies envisaged by Erhard Gaul (Reference Gaul2017).
3. CYLINDER TARGET PROPERTIES FOR A LASER BORON FUSION REACTOR
Laser ignition of fusion in a cylindrical fuel target is in indifference to the most studied spherical ignition (Hora, Reference Hora1964; Hora et al., Reference Hora, Azechi, Kitagawa, Mima, Murakami, Nakai, Nishihara, Takabe, Yamanaka, Yamanaka and Yamanaka1998, and see Chapter 9.4 of Hora, Reference Hora2016) with adiabatic plasma compression and thermal ignition. For cylindrical ignition, the studies of plane laser waves at normal incidence on a plane plasma target are of interest in one dimension. The computations are including the forces from the gasdynamic plasma pressure but on top, there is a further pressure from the electrodynamic laser field which can dominate over the thermal forces if the laser has a sufficiently high intensity. Figure 4 is the result where a deuterium plasma layer with critical density at x = 0 density not far from the solid state is irradiated by a neodymium glass laser with 1018 W/cm2 intensity from the right-hand side. The fully drawn line is the density of the laser energy given by the electric E and magnetic B field of the laser. The intensity at the vacuum at the right side end is increased in the plasma due to the optical constant like in glass resulting in an increase to a maximum, and into a deeper decay due to absorption similar to metallic absorption of light. The negative gradient of this curve produces a nonlinear (or ponderomotive) force in the plasma which is much larger than the gasdynamic force for an initial plasma temperature of about 1 million degree and despite further heating by the laser that all is carefully included in the computation. 1.5 ps after the laser interaction the non-thermal laser force accelerated the plasma to the velocities shown in the dashed line. There is a plasma block moving with a velocity above 109 cm/s against the laser light in the outer part and another block (negative velocity) moving into the deeper part of the deuterium. The acceleration for these blocks has the astronomical value above 1020 cm/s2.
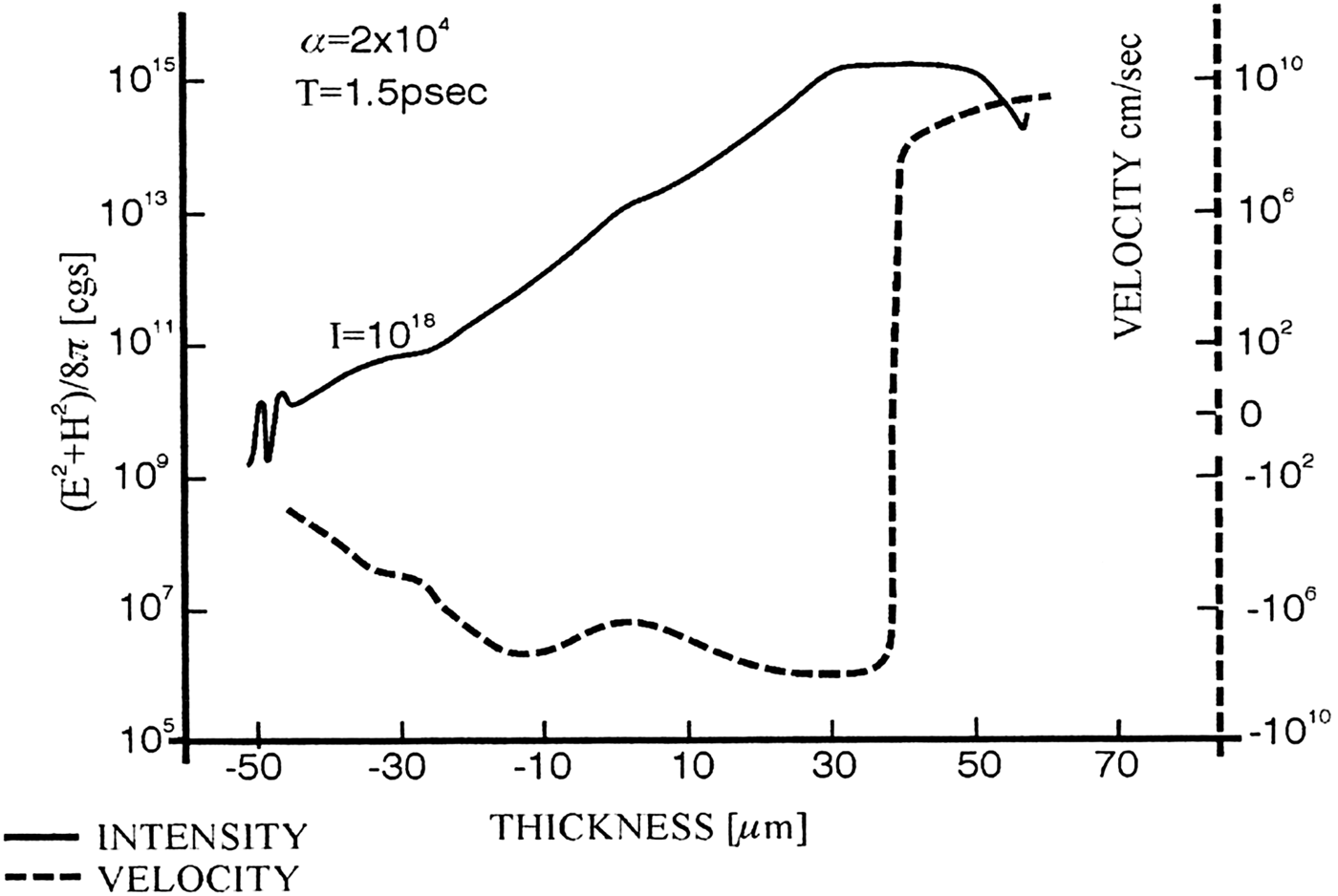
Fig. 4. An intensity of 1018 W/cm2 neodymium glass laser incident from the right-hand side on an initially 100 eV hot very low reflecting deuterium plasma profile produces after 1.5 ps two non-thermally driven plasma blocks by the non-linear (ponderomotive) force (Lawrence, Reference Lawrence1978), one block moving against the laser irradiated from the right-hand side and another block moving into the target interior (Fig. 8.4 of Hora, Reference Hora2016). The laser intensity is expressed by the energy density of the laser field (E 2 + H 2)/8π electric E and magnetic field H.
The result of Figure 4 was from computations in 1978 (Lawrence, Reference Lawrence1978; Hora, Reference Hora1981). The necessary picosecond laser pulses of the power of up to Petawatt were available only in 1996. The measurement of the plasma blocks was then possible, Figure 5 by Sauerbrey (Reference Sauerbrey1996) from the Doppler blue shift of spectral lines in the reflected light arriving at the theoretically predicted value of the ultrahigh acceleration above 1020 cm/s2. This was about 100,000 times higher than any acceleration measured in a laboratory. The experiment was not easy to be reproduced but well repeated soon by Földes et al. (Reference Földes, Bakos, Gal, Juhasz, Kedves, Koscis, Szatmari and Veres2000).
Fig. 5. Ultrahigh acceleration of plasma blocks by the dielectric explosion of laser pulses of picoseconds duration calculated in 1978 by non-thermal forces of laser interaction and measured by Sauerbrey (Reference Sauerbrey1996) as predicted (Hora, Reference Hora1981).
The nonlinear force-driven ultrahigh accelerated plasma blocks had a further extreme property. The space-charge neutral plasma blocks had ion current densities more than million times higher than any classical ion accelerator could produce. It was then possible that the picoseconds-Petawatt laser pulses produced the ultrahigh density accelerated ion pulses of few to several hundred MeV ions. This was measured in agreement with complicated computations. Interestingly the acceleration could be calculated in a transparent and understandable way by the genuine multi-fluid hydrodynamic models (Banati et al., Reference Banati, Hora, Lalousis and Moustaizis2014) needed for hadron cancer therapy. This completed hydrodynamics demonstrated for the first time directly (Lalousis & Hora, Reference Lalousis and Hora1983; Hora et al., Reference Hora, Lalousis and Eliezer1984; Eliezer et al., Reference Eliezer, Nissim, Martinez Val, Mima and Hora2014), how inhomogeneous plasmas have very high internally electric fields and their dynamic changes.
For ignition of laser fusion, the plasma blocks were needed for the first general use of the initiation of fusion reactions by picoseconds laser pulses irradiating uncompressed, solid-state fuel. Chu (Reference Chu1972) and Bobin (Reference Bobin, Schwarz and Hora1974) evaluated the laser properties for igniting uncompressed solid density fusion fuel. The result was that the initiation of a fusion reaction needed an impact of an energy flux of 4 × 108 J/cm2 during one picosecond as a threshold for generating a fusion flame in DT. For the computation, the above described nonlinear force driven plasma block generation could then be used and the later known plasma phenomena had to be included for reproducing the ignition of DT (Hora et al., Reference Hora, Malekynia, Ghoranneviss, Miley and He2008). It was then a surprise when using the fusion cross sections of HB11 were used in the calculations: The thresholds for B11 were nearly the same (Hora, Reference Hora2009; Hora et al. Reference Hora, Miley, Ghorannviss, Malekynia, Azizi and He2010) as for DT. Fusion ignition of HB11 was then happening at five orders of magnitudes higher thresholds than the classical HB11 fusion at thermal equilibrium. These computations used the single fluid hydrodynamics as Chu (Reference Chu1972). Using the genuine two-fluid code (Lalousis & Hora, Reference Lalousis and Hora1983; Hora et al., Reference Hora, Lalousis and Eliezer1984) arrived at the same ignition but with many more details of shock generation and thermal plasma effects beyond the analytical result of the Rankine-Hugoniot theory.
The reaction rate in solid state HB11 fuel depending on the depth x of the fuel at different times is shown in a case of Fig. 6. The reaction front moves with a velocity in the range of 1000 km/s which value is similar as known from explosive nuclear reactions. It is a remarkable generation of the shock density profile as it is building up very much later than the ps plasma block initiation of the reaction. This delay is 500 ps and more.
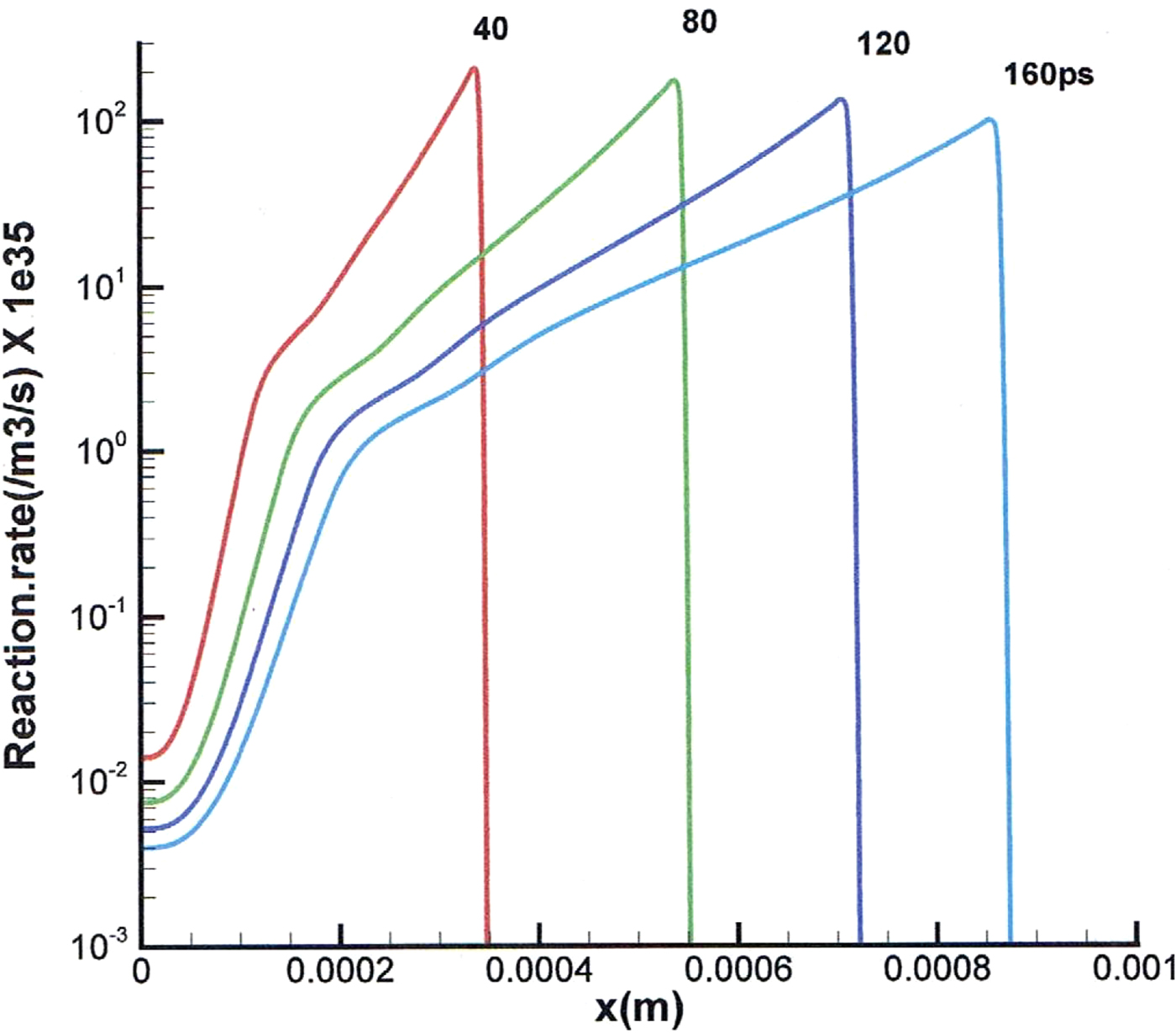
Fig. 6. HB11 fusion reaction rate at different depths x in 1D computation at times after the ps generation of the fusion flame initiated by a 1020 W/cm2, ps, 248-nm wavelength laser pulse.
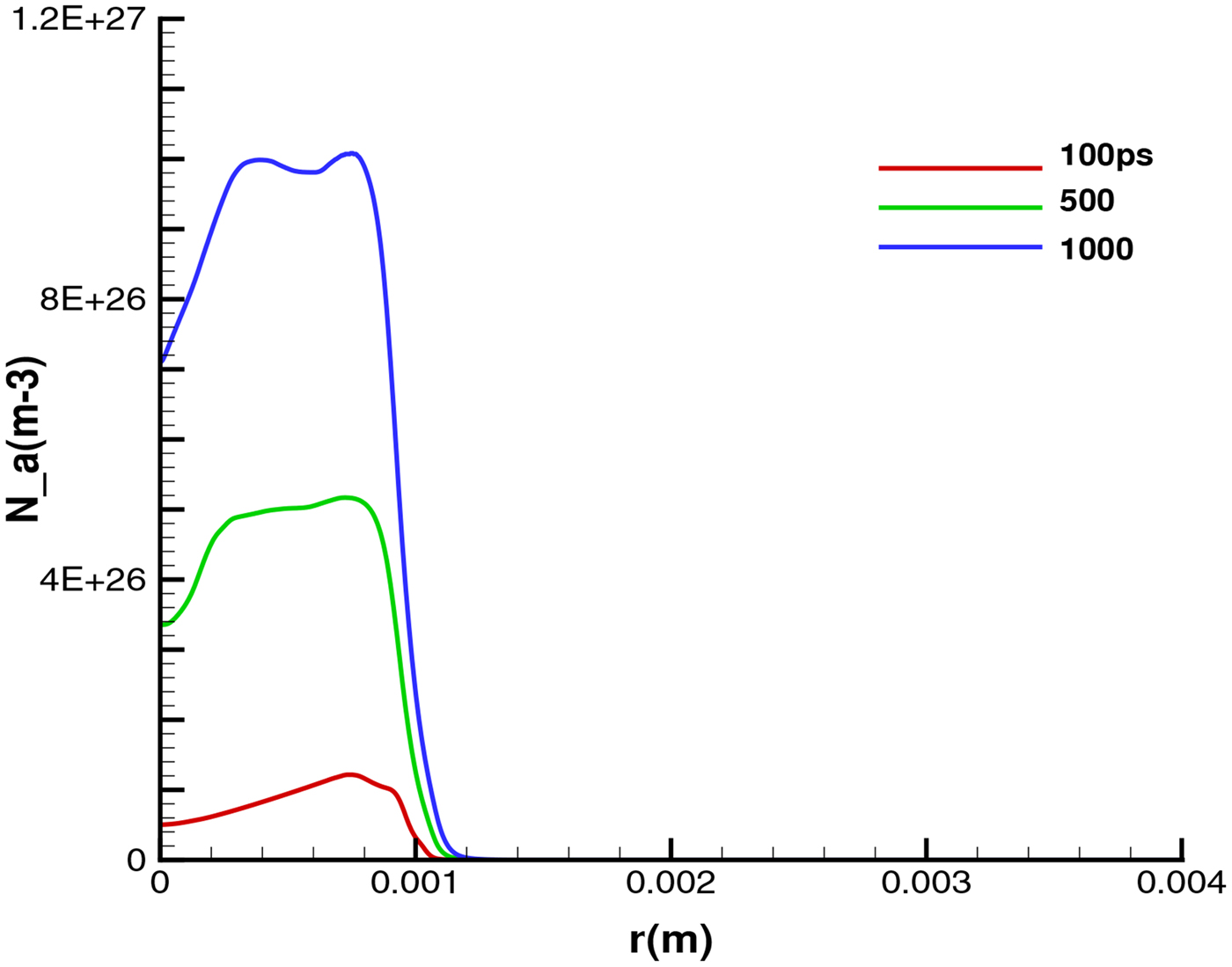
The one-dimensional (1D) conditions were nearly sufficiently well given in the experiments of Sauerbrey (Reference Sauerbrey1996) or later for clearly demonstrating that the generated plasma blocks were generated in the skin depth of the irradiated plasma (Badziak et al., Reference Badziak, Kozlov, Makowski, Paris and Ryc1999; Hora et al., Reference Hora, Badziak, Boody, Höpfl, Jungwirth, Kralikowa, Kraska, Laska, Parys, Perina, Pfeifer, Rohlena, Skala, Ullschmied, Wolowski and Woryna2002, Reference Hora, Badziak, Read, Li, Liang, Liu, Sheng, Zhang, Osman, Miley, Zhang, He, Peng, Osman, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied2007; Hora, Reference Hora2003) as seen from the unchanged numbers of the ion in the fast blocks at varying laser intensities at the same focusing. In order to take care of the restricted laser beam diameter and to produce a cylindrical geometry of the reaction as shown in Figure 3, the trapping of the reaction at a constant radius is necessary. This can be done by the ultrahigh magnetic field by the laser produced plasma with the plates as shown in Figure 3. Figure 7 shows the result of trapping of the plasmas to the initial radius of 1 mm by a magnetic field of 5 kilotesla is evident. The number of the generated alpha particles is shown at different times. The radial trapping at different times is confirmed and increasing on time indicating the successful ignition.
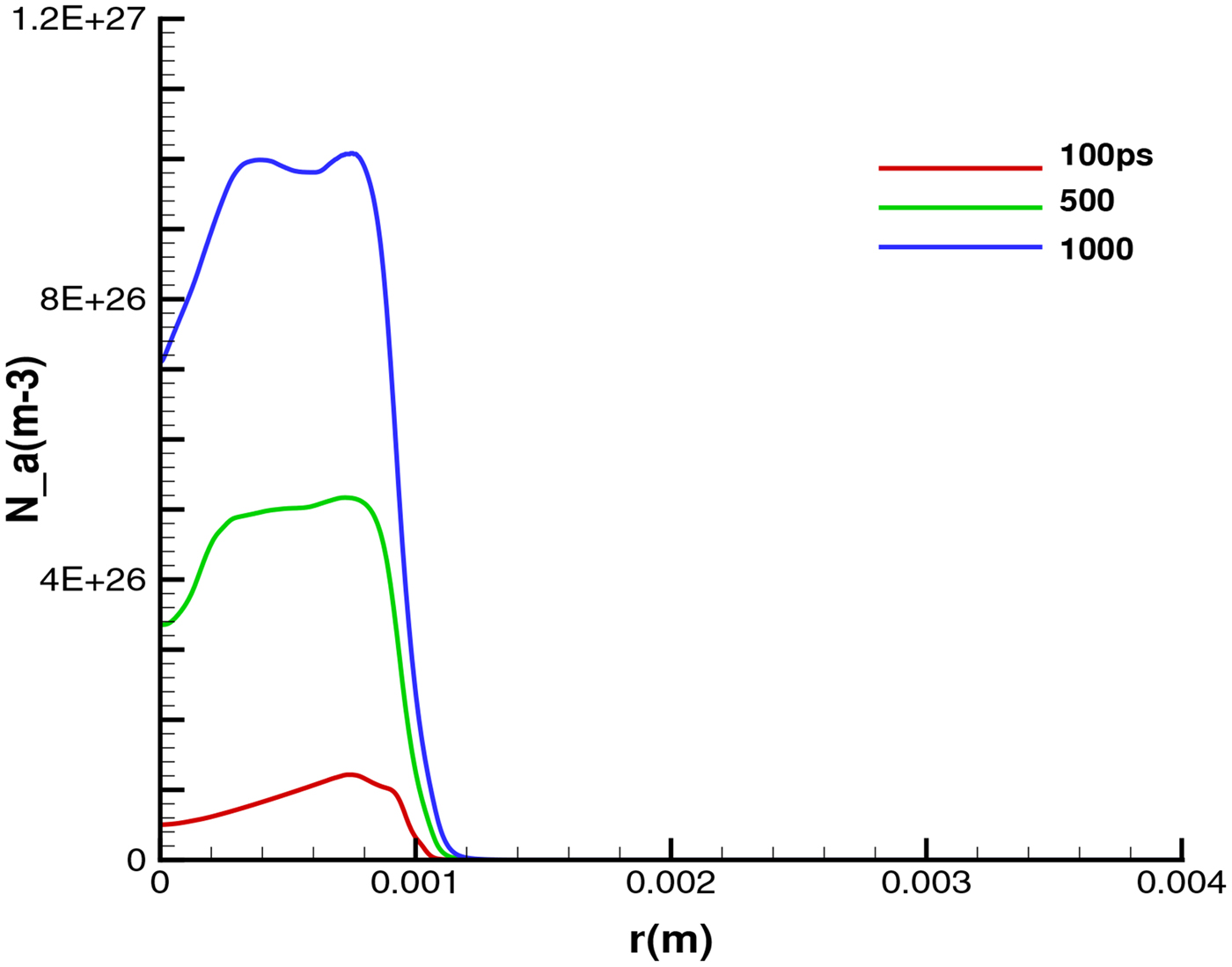
Fig. 7. Radial trapping of the plasma in a cylindrical reaction volume of Figure 3 where the density of the generated alpha particles, N_a, is shown at different times after the block ignition by the ps laser pulse.
Parallel to these developments with computations of binary fusion reactions for HB11 similar to the computations using DT, the measurements of highly increased fusion gains of with boron (Picciotto et al. Reference Picciotto, Margarone, Velyhan, Bellini, Krasa, Szydlowski, Bertuccio, Shi, Margarone, Prokupek, Malinowska, Krouski, Ullschmied, Laska, Kucharik and Korn2014; Margarone et al. Reference Margarone, Picciotto, Velyhan, Krasa, Kucharik, Mangione, Szydlowsky, Malinowska, Bertuccio, Shi, Crivellari, Ullschmied, Bellutti and Korn2015) was not only clarified by comparison with gains from DT for confirming the avalanche multiplication (Hora et al., Reference Hora, Lalousis and Moustaizis2014, Reference Hora, Korn, Giuffrida, Marganoone, Picciotto, Krasa, Jungwirth, Ullschmied, Lalouais, Eliezer, Miley, Moustaizis and Mourou2015a , Reference Hora, Lalousis, Giuffrida, Margarone, Korn, Eliezer, MILEYi, Moustaizis and Mourou b ) of generating each three alpha particles per reaction. Evaluating the experiments (Margarone et al., Reference Margarone, Picciotto, Velyhan, Krasa, Kucharik, Mangione, Szydlowsky, Malinowska, Bertuccio, Shi, Crivellari, Ullschmied, Bellutti and Korn2015) by elastic collisions within the extremely non-equilibrium plasma confirmed the avalanche process in all details (Eliezer et al., Reference Eliezer, Hora, Korn, Nissim and Martinez-Val2016), Figure 8.

Fig. 8. The three alpha particles of same energy produced by the HB11 reaction, Eq. (1), transfer their energy by elastic collisions with the low-energy boron or hydrogen nuclei of low temperature in the thermal non-equilibrium background plasmas (Eliezer et al., Reference Eliezer, Hora, Korn, Nissim and Martinez-Val2016).
Summarizing all the mentioned processes permitted the computation (Lalousis et al., Reference Lalousis, Hora and Moustaizis2014) that the single beam direct drive HB11 fusion in the cylindrically trapped fusion plasma with end-on direct drive plasma block ignition will produce a very high energy gain. The final result for a power reactor of Figure 2 (Hora, Reference Hora2015; Hora et al., Reference Hora2014, Reference Hora, Korn, Giuffrida, Marganoone, Picciotto, Krasa, Jungwirth, Ullschmied, Lalouais, Eliezer, Miley, Moustaizis and Mourou2015a , Reference Hora, Lalousis, Giuffrida, Margarone, Korn, Eliezer, MILEYi, Moustaizis and Mourou b ) will then result in the reaction of 14 milligram boron-11 with the protons of hydrogen generating more than one Gigajoule (GJ = 277 kWh) energy. The single laser beam for the ignition has to be a picoseconds laser pulse of 30 kJ energy of 30 PW power, which kind of pulses are rather close to the state of the art if needed one shot per second for energy generation of the value of more than $100 million/year (Hora et al., Reference Hora, Eliezer, Nissim, Xu and Lalousis2017b , Reference Hora, Eiezer, Wang, Korn, Nissim, Xu, Lalousis, Kirchhoff and Miley c ).
4. PROBLEMS TO BE SOLVED
The open problems for the single beam cylindrical HB11 fusion reaction are the detailed mechanisms in the ignited cylindrical reaction plasma. The basic step is the combination of the well-developed non-thermal equilibrium initiation of the reaction blocks driven by forces of the laser–plasma interaction, together with the new trapping kilotesla magnetic fields as the key process (Fujioka et al. Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi2013; Hora et al. Reference Hora, Lalousis and Moustaizis2014, Reference Hora, Eliezer, Nissim, Xu and Lalousis2017b ). The plasma block ignition is fully explored based on the initial fusion flame generation (Chu, Reference Chu1972; Bobin, Reference Bobin, Schwarz and Hora1974; Hora et al., Reference Hora, Malekynia, Ghoranneviss, Miley and He2008) using ultrahigh acceleration of plasma layers as measured from blue-shifted spectral lines (Sauerbrey, Reference Sauerbrey1996; Földes et al., Reference Földes, Bakos, Gal, Juhasz, Kedves, Koscis, Szatmari and Veres2000) is in exact agreement with theoretical predictions (Hora, Reference Hora1981; Hora, Reference Hora2016; Hora et al., Reference Hora, Badziak, Read, Li, Liang, Liu, Sheng, Zhang, Osman, Miley, Zhang, He, Peng, Osman, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied2007, Reference Hora, Malekynia, Ghoranneviss, Miley and He2008). The trapping of cylindrical targets by more than kilotesla magnetic fields was shown (Lalousis et al., Reference Hora, Lalousis and Moustaizis2014; Hora, Reference Hora2016) (Fig. 7) by computation under temporally constant conditions of the magnetic field.
In reality, the capacitor magnetic coil fields in Figure 3, are not constant and have a complicated spatial and temporal development while the fusion reaction process in the fuel – well evaluated for 1D geometry – will be modified. This flexibility will indeed give the chances for well advantageous conditions for selecting the best time frames for scheduling the block ignition of laser 2 with the constant timing of the laser 1 for operating the capacitor coil of Figure 3. These conditions have to be studied well with techniques available in established laboratories with sophisticated technologies parallel to specific computations using hydrodynamics or particle-in-cell PIC methods. The knowledge gained from this research will lead to generalizations of the properties of the laser pulse 1 with respect to focusing, time dependence and the incidence angle of the beam on the capacitor plates.
The extreme laser pulse 2 has, first of all, to be generated with a very perfectly controlled suppression of pre-pulses. Though these pulses are normally of 1 ps duration or shorter, their temporal pulse shape can well be modified by now available control. This also will give some variability for the temporal scheduling in view of magnetic field development under the control of Laser 1. These are rather sophisticated experimental tasks but are not new and have been solved before.
Another possibility to optimize the conditions for the fusion process of the conditions of the fuel may be if the magnetic field will not only be cylindrical symmetric geometry but may get an additional conical component by modifying the coils in Figure 3 in an asymmetric way with respect to the axis.
While studying the mentioned parameters, there is one question, how the fuel in Figure 3 is behaving within the ultrahigh magnetic fields, even without irradiation of the pulse from laser 2 for the fusion ignition. Under the growing magnetic field in the coil, it will be interesting to find out how the fuel substance – or any other material – will behave under the extreme magnetic fields before reaching the range of kilotesla and more. Will an ionization happen and under what magnetic field strengths? This kind of magnetic field ionization is a topic that may never have been studied before. If a plasma would be generated, or how this may be controllable by providing or reducing a certain electric conductivity in the fuel under the extreme conditions, this all may be a further new parameters that can be developed for optimizing the conditions of the new type of cylindrical fusion reactions in Figures 2 and 3 differing from the highly explored fusion in spherical fuel targets.
Progress in this research – but not as a condition of high priority or necessity – is the new direction to study the non-LTE conditions in plasmas as a basically new task for theory. The long desire of the environmentally clean HB11 reaction (excluding exceptional cases of higher energies for nuclear reactions) is of such high interest that all attempts are to be considered to achieve this, under the conditions of non-thermal equilibrium and using nonlinearities (Hora, Reference Hora1988). These conditions are best given by lasers using high plasma densities near the solid state and are fulfilled with the highest laser-fusion gains measured (Picciotto et al., Reference Picciotto, Margarone, Velyhan, Bellini, Krasa, Szydlowski, Bertuccio, Shi, Margarone, Prokupek, Malinowska, Krouski, Ullschmied, Laska, Kucharik and Korn2014), repeated and even increased by a factor 10 (Giuffrida et al., Reference Giuffrida, Scuderi, Cirrone, Margarone, Picciotto, Velyhan, Peringa, Miluzzo, Krasa, Dostal, Kucharik and Korn2017) and directly visible from the analysis using elastic nuclear collisions (Eliezer et al., Reference Eliezer, Hora, Korn, Nissim and Martinez-Val2016; Hora et al., Reference Hora, Eliezer, Nissim, Xu and Lalousis2017b , Reference Hora, Eiezer, Wang, Korn, Nissim, Xu, Lalousis, Kirchhoff and Miley c ). A very important new approach is the result of proving these non-equilibrium properties by theoretical evaluations of NIF-experiments (Fan et al., Reference Fan, Liu, Liu, Yu, Lan and Liu2017).
The research for low density plasmas for HB11 reactions (Hora et al., Reference Hora, Eliezer, Kirchhoff, Korn, Lalaousis, Miley and Moustaizis2017a ) is well under way, especially with the Tri-Alpha-Energy project (Rostoker & Binderbauer, Reference Rostoker and Binderbauer1996) of which the reverse magnetic field design is a modification of the cylindrical version of the Hirsch-Miley configuration of inertial electrostatic confinement IEC (see Section 2 of Hora et al., Reference Hora, Eliezer, Kirchhoff, Korn, Lalaousis, Miley and Moustaizis2017a ). With all these configurations, not any HB11 fusion was measured yet in these low-density plasmas, while the laser-experiments (Belyaev et al., Reference Belyaev, Matafonov, Vinogradov, Krainov, Lisitsa, Roussetski, Ignatyev and Andrianov2005; Labaune et al., Reference Labaune, Deprierraux, Goyon, Loisel, Yahia and Rafelski2013; Picciotto et al., Reference Picciotto, Margarone, Velyhan, Bellini, Krasa, Szydlowski, Bertuccio, Shi, Margarone, Prokupek, Malinowska, Krouski, Ullschmied, Laska, Kucharik and Korn2014) arrived at the super-high reaction gains above those from DT.
The extensive studies of plasmas since 1940 have gained an enormous amount of results with very numerous, unexpected discoveries where the new developing work on HB11 fusion is only one of the subdivisions. How this exploration of science is crucial for the enormous problems ahead, was very well envisioned by the formulations of the problems of plasmas by one of its greatest masters, Edward Teller, on the background also of the complex problems discovered and pioneered by Lord May of Oxford (Robert M. May) as fundamental orientation (see pages 2–4 of Hora, Reference Hora2016).
5. NEED FOR VERY HIGH CONTRAST RATIO OF PW-PS LASER PULSES
The experiments for the studies listed in the preceding section may be performed with lasers of the usual quality with PW-ps pulses. However, very extreme quality is necessary with respect to the contrast ratio for measuring the single beam initiation of the ignition process, characterized by the blue Doppler shift in the reflected light. These high-class laser beams were well available, but only in the very rare cases of with the KrF lasers used by Sauerbrey (Reference Sauerbrey1996) and Földes et al. (Reference Földes, Bakos, Gal, Juhasz, Kedves, Koscis, Szatmari and Veres2000) and by the extremely precisely developed solid-state lasers used by Zhang et al. (Reference Zhang, He, Chen, Li, Zhang, Wang, Feng, Zhang, Tang and Zhang1998) and by Badziak et al. (Reference Badziak, Kozlov, Makowski, Paris and Ryc1999). When Sauerbrey (Reference Sauerbrey1996) tried to repeat the measurements at Rutherford Appleton Laboratory with much more powerful KrF lasers in cooperation with many top class physicists, the results could not be reproduced. The same happened when Badziak was invited to use the solid-state lasers at the Ecole Polytechnique in Paris, the pioneering results of (Badziak et al., Reference Badziak, Kozlov, Makowski, Paris and Ryc1999) this could not be reproduced. The reason was very evident: The lasers for the reproduction were not good enough!
For using the single beam ignition of the HB11 fusion, see Figures 2 and 3 in difference from multi-beams for spherical irradiation, Figure 1, the fusion fuel is not spherical (Hora et al., Reference Hora, Azechi, Kitagawa, Mima, Murakami, Nakai, Nishihara, Takabe, Yamanaka, Yamanaka and Yamanaka1998), but of cylindrical geometry, Figure 5, with trapping the reaction plasma by ultrahigh magnetic fields (Fujioka et al., Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi2013) of several kilotesla. Use is then made from the extensively studied non-thermal driving of plasma bocks by the nonlinear force, Figure 4 [see Fig. 8.4 from Hora (Reference Hora2016) drawn from Figs. 10.18a & b of Hora (Reference Hora1981)]. The 105 times higher acceleration than ever measured before in a laboratory for interacting within pico-second laser pulses giving velocities of more than 1000 km/s, was measured from the blue Doppler-shift of reflected spectral lines (Sauerbrey, Reference Sauerbrey1996; Földes et al., Reference Földes, Bakos, Gal, Juhasz, Kedves, Koscis, Szatmari and Veres2000). This blue-shift is in exact agreement with the theoretical predictions from the hydrodynamic computations (Hora, Reference Hora1981; Hora et al., Reference Hora, Badziak, Read, Li, Liang, Liu, Sheng, Zhang, Osman, Miley, Zhang, He, Peng, Osman, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied2007).
The cylindrical fusion fuel is shown in the axis of the coils of Figure 3 and the irradiation by the single igniting laser pulse is shown end-on at the cylinder of the fuel. The details of the description of the HB11 reactor are based on extensive results of the plane-wave plasma-block generation with detailed experimental and theoretical confirmation. It should be noticed that the new HB11 clean fusion reactor may be listed under the category of fast ignition by Tabak et al. (Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason1994) but it is essentially different from usual schemes as no plasma compression etc. is needed for the new HB11 case.
For designing the next following experimental confirmation of the ignition processes by >PW–ps laser pulses it is necessary to underline the required extremely high contrast ratio of these laser pulses. This contrast has been verified in the preceding experiments and can be taken over from there, but this needed very sophisticated laser technology. It has been achieved in the experiments with KrF excimer lasers (Sauerbrey, Reference Sauerbrey1996) and only the most exceptional attention and experience did clarify the conditions for excluding relativistic self-focusing by using solid-state lasers (Zhang et al., Reference Zhang, He, Chen, Li, Zhang, Wang, Feng, Zhang, Tang and Zhang1998) convincingly demonstrated by Jie Zhang. It is important to note that the solid-state lasers used in this extremely high contrast were fulfilled in the unique experiments showing the nonlinear-force driven plasma-block acceleration directly from the skin-layer acceleration (Hora et al., Reference Hora, Badziak, Boody, Höpfl, Jungwirth, Kralikowa, Kraska, Laska, Parys, Perina, Pfeifer, Rohlena, Skala, Ullschmied, Wolowski and Woryna2002; Hora, Reference Hora2003). Repeating these experiments in other countries by the same experts did fail due to the insufficient quality of the used lasers with respect to contrast properties. This insufficient quality of the usual laser pulses can be seen from the broad stream experiments resulting in a red Doppler-shift instead of the blue shift. This could be understood by using PIC computations with plasma densities below critical. The very difficult calculations at critical density were mastered only by JW Wang and his team recently (Xu et al., Reference Xu, Wang, Qi, Li, Xing and Long2016, Reference Xu, Wang, Qi, Li, Xing, Long and Zhu2017; Li et al., Reference Li, Wang, Xu and Zhu2017; Hora et al., Reference Hora, Eiezer, Wang, Korn, Nissim, Xu, Lalousis, Kirchhoff and Miley2017c ).
As a test whether the PW-ps laser pulses have a sufficient contrast ratio may be that the light reflected from the irradiated target has to show a blue Doppler shift of spectral lines. Any other lasers cannot be used for studying the non-thermal plasma block ignition at the direct drive on the cylindrical end of theHB11 fuel. When checking earlier experiments, it was elaborated (Hora, Reference Hora2003) that the extremely unique laser-fusion experiments by Norreys et al. (Reference Norreys, Fews, Beg, Bell, Dangor, Lee, Nelson, Schmidt, Tatarakis and Cable1998) and Clark et al. (Reference Clark, Krushelnik, Zepf, Tataralis, Machacek, Santla, Watts, Norreys and Dangor2001) were so exceptional and significant because there seemed to be at least for a short period, laser pulses available with the extreme contrast conditions. When re-evaluating the fusion gain with a 100:1 increase when estimating the DT value from DD, the absolute record gain of about 0.3 was achieved. This is the highest than ever produced gains by laser driven fusion and the highest gains ever reported from tokamak experiments (see p. 218 of Hora, Reference Hora2016).
ACKNOWLEDGMENTS
The authors involved with the here given elaboration for the next steps for a laser boron fusion reactor gratefully acknowledge the work of the authors in the cited preceding contributions, especially to L. Giuffrida et al. (2017) for guiding the cooperation by Prof. Georg Korn, Prof. Karel Jungwirth and Dr. Jiri Ullschmied at the European ELI-Beams Project and the PALS Laser of the Academy of Science of the Czech Republic in Prague.