Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-23T18:21:33.272Z Has data issue: false hasContentIssue false
  • English
  • Français

Random zeros on complex manifolds: conditional expectations

Part of: Holomorphic fiber spaces

Published online by Cambridge University Press:  11 March 2011

Bernard Shiffman ,
Steve Zelditch  and
Qi Zhong
Bernard Shiffman
Affiliation:
Department of Mathematics, Johns Hopkins University, Baltimore, MD 21218, USA (shiffman@math.jhu.edu)
Steve Zelditch
Affiliation:
Department of Mathematics, Northwestern University, Evanston, IL 60208, USA (zelditch@math.northwestern.edu)
Qi Zhong
Affiliation:
Department of Mathematics, Vanderbilt University, Nashville, TN 37240, USA (qi.zhong@vanderbilt.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the conditional distribution 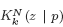of zeros of a Gaussian system of random polynomials (and more generally, holomorphic sections), given that the polynomials or sections vanish at a point p (or a fixed finite set of points). The conditional distribution is analogous to the pair correlation function of zeros but we show that it has quite a different small distance behaviour. In particular, the conditional distribution does not exhibit repulsion of zeros in dimension 1. To prove this, we give universal scaling asymptotics for 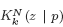around p. The key tool is the conditional Szegő kernel and its scaling asymptotics.

Keywords

random holomorphic sectionszeros of random polynomialsholomorphic line bundleKähler manifoldSzegő kernel

MSC classification

Secondary: 32L10: Sheaves and cohomology of sections of holomorphic vector bundles, general results
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 10 , Special Issue 3: A Special Issue in Honour of Louis Boutet de Monvel and Pierre Schapira , July 2011 , pp. 753 - 783
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bleher, P., Shiffman, B. and Zelditch, S., Universality and scaling of correlations between zeros on complex manifolds, Invent. Math. 142 (2000), 351–395.CrossRefGoogle Scholar
2.Bleher, P., Shiffman, B., and Zelditch, S., Correlations between zeros and supersymmetry, Dedicated to Joel L. Lebowitz, Commun. Math. Phys. 224 (2001), 255–269.CrossRefGoogle Scholar
3.Catlin, D., The Bergman kernel and a theorem of Tian, in Analysis and geometry in several complex variables (ed. Komatsu, G. and Kuranishi, M.) (Birkhäuser, Boston, MA, 1999).Google Scholar
4.Deift, P. A., Orthogonal polynomials and random matrices: a Riemann-Hilbert approach, Courant Lecture Notes in Mathematics, Volume 3 (American Mathematical Society, Providence, RI, 1999).Google Scholar
5.Demailly, J. P., Complex analytic and differential geometry, book manuscript (2009) (http:\\www-fourier.ujf-grenoble.fr/~demailly/manuscripts/agbook.pdf).Google Scholar
6.Federer, H., Geometric measure theory (Springer, 1969).Google Scholar
7.Griffiths, P. and Harris, J., Principles of algebraic geometry (Wiley-Interscience, New York, 1978).Google Scholar
8.Janson, S., Gaussian Hilbert spaces, Cambridge Tracts in Mathematics, Volume 129 (Cambridge University Press, 1997).Google Scholar
9.Kallenberg, O., Foundations of modern probability, 2nd edn, Probability and Its Applications (Springer, 2002).Google Scholar
10.Shiffman, B. and Sommese, A. J., Vanishing theorems on complex manifolds, Progress in Mathematics, Volume 56 (Birkhäuser, Boston, MA, 1985).Google Scholar
11.Shiffman, B. and Zelditch, S., Distribution of zeros of random and quantum chaotic sections of positive line bundles, Commun. Math. Phys. 200 (1999), 661–683.CrossRefGoogle Scholar
12.Shiffman, B. and Zelditch, S., Asymptotics of almost holomorphic sections of ample line bundles on symplectic manifolds, J. Reine Angew. Math. 544 (2002), 181–222.Google Scholar
13.Shiffman, B. and Zelditch, S., Number variance of random zeros on complex manifolds, Geom. Funct. Analysis 18 (2008), 1422–1475.CrossRefGoogle Scholar
14.Soshnikov, A., Level spacings distribution for large random matrices: Gaussian fluctuations, Annals Math. (2) 148 (1998), 573–617.CrossRefGoogle Scholar
15.Stoll, W., The continuity of the fiber integral, Math. Z. 95 (1967), 87–138.CrossRefGoogle Scholar
16.Zeitouni, O. and Zelditch, S., Large deviations of empirical measures of zeros of random polynomials, Int. Math. Res. Not. 2010 (2010), 3935–3992.Google Scholar
17.Zelditch, S., Szegő Kernels and a theorem of Tian, Int. Math. Res. Not. 1998 (1998), 317–331.CrossRefGoogle Scholar