Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-20T05:16:57.293Z Has data issue: false hasContentIssue false
  • English
  • Français

POLISH MODELS AND SOFIC ENTROPY

Part of: General theory of linear operators Ergodic theory Selfadjoint operator algebras

Published online by Cambridge University Press:  18 January 2016

Ben Hayes
Ben Hayes*
Affiliation:
Stevenson Center, Nashville, TN 37240, USA (benjamin.r.hayes@vanderbilt.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

We deduce properties of the Koopman representation of a positive entropy probability measure-preserving action of a countable, discrete, sofic group. Our main result may be regarded as a ‘representation-theoretic’ version of Sinaǐ’s factor theorem. We show that probability measure-preserving actions with completely positive entropy of an infinite sofic group must be mixing and, if the group is nonamenable, have spectral gap. This implies that if 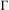$\unicode[STIX]{x1D6E4}$ is a nonamenable group and 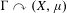$\unicode[STIX]{x1D6E4}\curvearrowright (X,\unicode[STIX]{x1D707})$ is a probability measure-preserving action which is not strongly ergodic, then no action orbit equivalent to 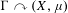$\unicode[STIX]{x1D6E4}\curvearrowright (X,\unicode[STIX]{x1D707})$ has completely positive entropy. Crucial to these results is a formula for entropy in the presence of a Polish, but a priori noncompact, model.

Keywords

sofic entropySinaǐ’s factor theoremnoncommutative harmonic analysis

MSC classification

Primary: 37A35: Entropy and other invariants, isomorphism, classification 47A67: Representation theory 37A55: Relations with the theory of $C^*$-algebras 46L89: Other “noncommutative” mathematics based on $C^*$-algebra theory
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 2 , April 2018 , pp. 241 - 275
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alpeev, A., On Pinsker factors for Rokhlin entropy, in Representation Theory, Dynamical Systems, Combinatorial Methods. Part XXIV, Zap. Nauchn. Sem. POMI, Volume 432, pp. 30–35 (St. Petersburg, 2015). POMI.Google Scholar
Bourgain, J. and Gamburd, A., On the spectral gap for finitely-generated subgroups of SU (2), Invent. Math. 171(1) (2008), 83–121.Google Scholar
Bourgain, J. and Gamburd, A., Uniform expansion bounds for cayley graphs of SL 2(F p ), Ann. of Math. (2) 167(2) (2008), 625–642.Google Scholar
Bourgain, J. and Yehudayof, A., Expansion in SL 2(ℝ) and monotone expanders, Geom. Funct. Anal. 23(1) (2013), 1–41.Google Scholar
Bowen, R., Entropy for group endomorphisms, Trans. Amer. Math. Soc. 153 (1971), 401–414.Google Scholar
Bowen, L., Measure conjugacy invariants for actions of countable sofic groups, J. Amer. Math. Soc. 23 (2010), 217–245.CrossRefGoogle Scholar
Bowen, L., A new measure conjugacy invariant for actions of free groups, Ann. of Math. (2) 171(2) (2010), 1387–1400.Google Scholar
Bowen, L., Entropy theory for sofic groupoids I: the foundations, J. Anal. Math. 124(1) (2014), 149–233.Google Scholar
Bowen, L. and Li, H., Harmonic models and spanning forests of residually finite groups, J. Funct. Anal. 263(7) (2012), 1769–1808.Google Scholar
Brown, N. and Ozawa, N., C ∗ -Algebras and Finite-Dimensional Approximations (Cambridge University Press, Providence, RI, 1994).Google Scholar
Burton, P., Naive entropy of dynamical systems, Preprint, 2015, arXiv:1503.06360.Google Scholar
Ciobanu, L., Holt, D. and Rees, S., Sofic groups: graph products and graphs of groups, Pacific J. Math. 271(1) (2014), 53–64. November.Google Scholar
Connes, A., Feldman, J. and Weiss, B., An amenable equivalence relations is generated by a single transformation, Ergodic Theory Dynam. Systems 10(4) (1983), 431–450.Google Scholar
Conway, J., A Course in Functional Analysis, 2nd ed., Graduate Texts in Mathematics, (Springer, New York, 2000).Google Scholar
Dooley, A. and Golodets, V., The spectrum of completely positive entropy actions of countable amenable groups, J. Funct. Anal. 196(1) (2002), 1–18.Google Scholar
Dykema, K., Kerr, D. and Pichot, M., Orbit equivalence and sofic approximation, Preprint, 2011, arXiv:1102.2556.Google Scholar
Dykema, K., Kerr, D. and Pichot, M., Sofic dimension for discrete measurable groupoids, Trans. Amer. Math. Soc. 366(2) (2013), 707–748.Google Scholar
Elek, G. and Szabo, E., On sofic groups, J. Group Theory 9(2) (2006), 161–171.Google Scholar
Hayes, B., Fuglede–Kadison determinants and sofic entropy, Preprint, 2014, arXiv:1402.1135.Google Scholar
Hayes, B., An l p -version of von neumann dimension for Banach space representations of sofic groups, J. Funct. Anal. 266(2) (2014), 989–1040.Google Scholar
Hayes, B., Mixing and spectral gap relative to Pinsker factors for sofic groups, Preprint, 2015, arXiv:1509.07839.Google Scholar
Ioana, A., Orbit equivalence and borel reducibility rigidity for profinite actions with spectral gap, Preprint, 2013, arXiv:1309.3026.Google Scholar
Kerr, D., Sofic measure entropy via finite partitions, Groups Geom. Dyn. 7 (2013), 617–632.Google Scholar
Kerr, D. and Li, H., Bernoulli actions and infinite entropy, Groups Geom. Dyn. 5 (2011), 663–672.Google Scholar
Kerr, D. and Li, H., Topological entropy and the variational principle for actions of sofic groups, Invent. Math. 186 (2011), 501–558.Google Scholar
Kerr, D. and Li, H., Soficity, amenability, and dynamical entropy, Amer. J. Math. 135(3) (2013), 721–761.Google Scholar
Kerr, D. and Li, H., Combinatorial independence and sofic entropy, Comm. Math. Stat. 1(2) (2014), 213–257.Google Scholar
Kieffer, J., A generalized Shannon–McMillan theorem for the action of an amenable group on a probability space, Ann. Probab. 3(6) (1975), 1031–1037.CrossRefGoogle Scholar
Li, H., Compact group automorphisms, addition formulas and Fuglede–Kadison determinants, Ann. of Math. (2) 176(1) (2012), 303–347.Google Scholar
Li, H., Sofic mean dimension, Adv. Math. 244 (2014), 570–604.Google Scholar
Lubotzky, A., Phillips, R. and Sarnak, P., Ramanujan graphs, Combinatorica 8(3) (1988), 261–277.Google Scholar
Margulis, G., Some remarks on invariant means, Monatsh. Math. 90(3) (1980), 233–234.Google Scholar
Meyerovitch, T., Positive sofic entropy implies finite stabilizer, Preprint, 2015, arXiv:1504.08137.Google Scholar
Ornstein, D. and Weiss, B., Ergodic theory of amenable groups I. The Rokhlin lemma, Bull. Amer. Math. Soc. (N.S.) 2(1) (1980), 161–165.Google Scholar
Ornstein, D. and Weiss, B., Entropy and isomorphism theorems for actions of amenable groups, J. Anal. Math. 48 (1987), 1–141.Google Scholar
Paunescu, L., On sofic actions and equivalence relations, J. Funct. Anal. 261(9) (2011), 2461–2485. November.CrossRefGoogle Scholar
Popa, S., On the superrigidity of malleable actions with spectral gap, J. Amer. Math. Soc. 21(4) (2008), 981–1000.Google Scholar
Popa, S., Independence properties in sublagebras of ultraproduct II1 factors, J. Funct. Anal. 266(9) (2014), 5818–5846.CrossRefGoogle Scholar
Selberg, A., On the estimation of Fourier coefficients of modular forms, in Proc. Sympos. Pure Math, Volume 8, pp. 1–15 (American Mathematical Society, Providence, RI, 1965).Google Scholar
Seward, B., Krieger’s finite generator theorem for ergodic actions of countable groups I, Preprint, 2014, arXiv:1405.3604.Google Scholar
Seward, B., Finite entropy actions of free groups, rigidity of stabilizers, and a Howe–Moore type phenomenon, J. Anal. Math., to appear.Google Scholar
Sinaǐ, J., On a weak isomorphism of transformations with invariant measure., Mat. Sb. (N.S.) 63(105) (1964), 23–42.Google Scholar
Sullivan, D., For n > 3 there is only one finitely additive rotationally invariant measure on the n-sphere on all Lebesgue measurable sets, Bull. Amer. Math. Soc. 4(1) (1981), 121–123.Google Scholar
Varadarajan, V., Measure on topological spaces, Mat. Sb. (N.S.) 55(97) (1961), 35–100.Google Scholar