Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-05-11T12:09:59.924Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE EXISTENCE OF NON-NORM-ATTAINING OPERATORS

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  09 July 2021

Sheldon Dantas ,
Mingu Jung Open the ORCID record for Mingu Jung [Opens in a new window]  and
Gonzalo Martínez-Cervantes Open the ORCID record for Gonzalo Martínez-Cervantes [Opens in a new window]
Sheldon Dantas
Affiliation:
Departament de Matemàtiques and Institut Universitari de Matemàtiques i Aplicacions de Castelló (IMAC), Universitat Jaume I, Campus del Riu Sec. s/n, 12071 Castelló Spain (dantas@uji.es)
Mingu Jung*
Affiliation:
Basic Science Research Institute and Department of Mathematics, POSTECH, Pohang 790-784, Republic of Korea
Gonzalo Martínez-Cervantes
Affiliation:
Universidad de Murcia, Departamento de Matemáticas, Campus de Espinardo 30100 Murcia, Spain (gonzalo.martinez2@um.es)
*
jmingoo@postech.ac.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

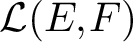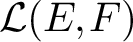In this article, we provide necessary and sufficient conditions for the existence of non-norm-attaining operators in $\mathcal {L}(E, F)$ . By using a theorem due to Pfitzner on James boundaries, we show that if there exists a relatively compact set K of $\mathcal {L}(E, F)$ (in the weak operator topology) such that 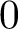$0$ is an element of its closure (in the weak operator topology) but it is not in its norm-closed convex hull, then we can guarantee the existence of an operator that does not attain its norm. This allows us to provide the following generalisation of results due to Holub and Mujica. If E is a reflexive space, F is an arbitrary Banach space and the pair 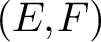$(E, F)$ has the (pointwise-)bounded compact approximation property, then the following are equivalent:

  1. (i) 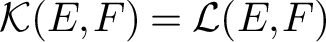$\mathcal {K}(E, F) = \mathcal {L}(E, F)$ ;

  2. (ii) Every operator from E into F attains its norm;

  3. (iii) 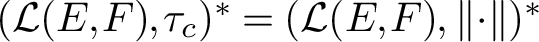$(\mathcal {L}(E,F), \tau _c)^* = (\mathcal {L}(E, F), \left \Vert \cdot \right \Vert )^*$ ,

where 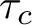$\tau _c$ denotes the topology of compact convergence. We conclude the article by presenting a characterisation of the Schur property in terms of norm-attaining operators.

Keywords

James theoremnorm-attaining operatorscompact approximation property

MSC classification

Primary: 46B20: Geometry and structure of normed linear spaces
Secondary: 46B10: Duality and reflexivity 46B28: Spaces of operators; tensor products; approximation properties
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 3 , May 2023 , pp. 1023 - 1035
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albiac, F. and Kalton, N., Topics in Banach Space Theory, 2nd ed., Graduate Texts in Mathematics, Vol. 233 (Springer, New York, 2016).CrossRefGoogle Scholar
Amir, D. and Lindenstrauss, J., The structure of weakly compact sets in Banach spaces, Ann. Math. 88 (1968), 35–44.CrossRefGoogle Scholar
Bonde, E., The approximation property for a pair of Banach spaces, Math. Scand. 57 (1985), 375–385.CrossRefGoogle Scholar
Casazza, P. G., Approximation properties, in Handbook of the Geometry of Banach Spaces, Vol. 1, Johnson, W. B. and Lindenstrauss, J., eds. (Elsevier, Amsterdam, 2001), pp. 271–316.CrossRefGoogle Scholar
Cho, C. and Johnson, W. B., A characterization of subspaces $X$ of ${\ell}_p$ for which $K(X)$ is an $M$ -ideal in $L(X)$ , Proc. Amer. Math. Soc. 93(3) (1985), 466–470.Google Scholar
Davie, A. M., The approximation problem for Banach spaces, Bull. London Math. Soc. 5 (1973), 261–266.CrossRefGoogle Scholar
Davis, W. J., Figiel, T., Johnson, W. B. and Pełczyński, A., Factoring weakly compact operators, J. Funct. Anal. 17 (1974), 311–327.CrossRefGoogle Scholar
Defant, A. and Floret, K., Tensor Norms and Operator Ideals (Elsevier, North-Holland, Amsterdam, 1993).Google Scholar
Dowling, P. N., Freeman, D., Lennard, C. J. Odell, E., Randrianantoanina, B., Turett, B., A weak Grothendieck compactness principle, J. Funct. Anal. 263 (2012), 1378–1381.CrossRefGoogle Scholar
Dunford, N. and Schwartz, J. T., Linear Operators, Part I, Wiley-Interscience, New York, 1958.Google Scholar
Fabian, M., Habala, P., Hájek, P., Montesinos, V. and Zizler, V., Banach Space Theory: The Basis for Linear and Nonlinear Analysis, CMS Books in Mathematics (Springer New York, 2010).Google Scholar
Feder, M. and Saphar, P., Spaces of compact operators and their dual spaces, Isr. J. Math. 21 (1975), 239–247.CrossRefGoogle Scholar
Grønbœk, N. and Willis, G. A., Approximate identities in Banach algebras of compact operators, Can. Math. Bull. 36 (1993), 45–53.Google Scholar
Grothendieck, A., Produits tensoriels topologiques et espaces nucléaires, Mem. Amer. Math. Soc. 16 (1955).Google Scholar
Guirao, A. J., Montesinos, V. and Zizler, V., Open Problems in the Geometry and Analysis of Banach Spaces, Springer International Publishing, Switzerland, 2016.Google Scholar
Holub, J. R., Reflexivity of $L\left(E,\ F\right)$ , Proc. Amer. Math. Soc. 39 (1973), 175–177.Google Scholar
James, R. C., Reflexivity and the supremum of linear functionals, Ann. Math., 66 (1957), 159–169.CrossRefGoogle Scholar
James, R. C., Reflexivity and the sup of linear functionals, Isr. J. Math. 13 (1972), 289–300.CrossRefGoogle Scholar
Johnson, W. B., Lillemets, R. and Oja, E., Representing completely continuous operators through weakly $\infty$ -compact operators, Bull. London Math. Soc. 48 (2016), 452–456.CrossRefGoogle Scholar
Khatskevich, V. A., Ostrovskii, M. I. and Shulman, V. S., Extremal problems for operators in Banach spaces arising in the study of linear operator pencils, Integr. Equ. Oper. Theory 51 (2005), 109–119.CrossRefGoogle Scholar
Lima, A. and Oja, E., Metric approximation properties and trace mappings, Math. Nachr. 280 (2007), 571–580.CrossRefGoogle Scholar
Lindenstrauss, J. and Tzafriri, L., Clasical Banach Spaces I, Sequence Spaces (Springer, Berlin, 1977).Google Scholar
Lindenstrauss, J. and Tzafriri, L. Classical Banach Spaces II, Function Spaces (Springer, Berlin, 1979).Google Scholar
Maslyuchenko, V. K. and Plichko, A. M., Some open problems on functional analysis and function theory, Extracta Math., 20 (2005), 51–70.Google Scholar
Mujica, J., Reflexive spaces of homogeneous polynomials, Bull. Polish Acad. Sci. Math. 49 (2001), 211–222.Google Scholar
Oja, E., Lifting bounded approximation properties from Banach spaces to their dual spaces, J. Math. Anal. Appl. 323 (2006), 666–679.CrossRefGoogle Scholar
Pfitzner, H., Boundaries for Banach spaces determine weak compactness, Invent. Math. 182 (2010), 585–604.CrossRefGoogle Scholar
Pietsch, A., Operator Ideals (Deutscher Verlag der Wissenschaften, Berlin, 1978).Google Scholar
Reinov, O. I., How bad can a Banach space with the approximation property be?, Mat. Zametki 33 (1983), 833–846 (in Russian); English translation in Math. Notes 33 (1983), 427–434.Google Scholar
Ruckle, W., Reflexivity of $L\left(E,F\right)$ , Proc. Amer. Math. Soc. 34 (1972), 171–174.Google Scholar
Sinha, D. P. and Karn, A. K., Compact operators whose adjoints factor through subspaces of ${\ell}_p$ , Studia Math. 150 (2002), 17–33.Google Scholar