Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-25T02:00:45.339Z Has data issue: false hasContentIssue false
  • English
  • Français

ON BOUNDED-TYPE THIN LOCAL SETS OF THE TWO-DIMENSIONAL GAUSSIAN FREE FIELD

Part of: Stochastic processes Markov processes

Published online by Cambridge University Press:  27 April 2017

Juhan Aru ,
Avelio Sepúlveda  and
Wendelin Werner
Juhan Aru
Affiliation:
Department of Mathematics, ETH Zürich, Rämistr. 101, 8092 Zürich, Switzerland (juhan.aru@math.ethz.ch; leonardo.sepulveda@math.ethz.ch; wendelin.werner@math.ethz.ch)
Avelio Sepúlveda
Affiliation:
Department of Mathematics, ETH Zürich, Rämistr. 101, 8092 Zürich, Switzerland (juhan.aru@math.ethz.ch; leonardo.sepulveda@math.ethz.ch; wendelin.werner@math.ethz.ch)
Wendelin Werner
Affiliation:
Department of Mathematics, ETH Zürich, Rämistr. 101, 8092 Zürich, Switzerland (juhan.aru@math.ethz.ch; leonardo.sepulveda@math.ethz.ch; wendelin.werner@math.ethz.ch)
Get access Rights & Permissions [Opens in a new window]

Abstract

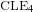We study certain classes of local sets of the two-dimensional Gaussian free field (GFF) in a simply connected domain, and their relation to the conformal loop ensemble $\text{CLE}_{4}$ and its variants. More specifically, we consider bounded-type thin local sets (BTLS), where thin means that the local set is small in size, and bounded type means that the harmonic function describing the mean value of the field away from the local set is bounded by some deterministic constant. We show that a local set is a BTLS if and only if it is contained in some nested version of the 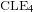$\text{CLE}_{4}$ carpet, and prove that all BTLS are necessarily connected to the boundary of the domain. We also construct all possible BTLS for which the corresponding harmonic function takes only two prescribed values and show that all these sets (and this includes the case of 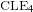$\text{CLE}_{4}$) are in fact measurable functions of the GFF.

Keywords

Random fieldsSchramm–Loewner evolutions

MSC classification

Primary: 60G60: Random fields 60J67: Stochastic (Schramm-)Loewner evolution (SLE)
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 3 , May 2019 , pp. 591 - 618
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aru, J., Lupu, T. and Sepúlveda, A., First passage sets of the 2D continuum Gaussian free field (in preparation).Google Scholar
Aru, J. and Sepúlveda, A., Two-valued local sets of the 2D continuum Gaussian free field: connectivity, labels and induced metrics (in preparation).Google Scholar
Dubédat, J., Commutation relations for Schramm–Loewner evolutions, Commun. Pure Appl. Math. 60 (2007), 1792–1847.Google Scholar
Dubédat, J., SLE and the free field: partition functions and couplings, J. Am. Math. Soc. 22 (2009), 995–1054.Google Scholar
He, Z.-X. and Schramm, O., Fixed points, Koebe uniformization and circle packings, Ann. Math. 137 (1995), 369–406.Google Scholar
Hu, X., Miller, J. and Peres, Y., Thick points of the Gaussian free field, Ann. Probab. 38 (2010), 896–926.Google Scholar
Izyurov, K. and Kytölä, K., Hadamard’s formula and couplings of SLEs with free field, Probab. Theory Related Fields 155 (2013), 35–69.Google Scholar
Miller, J. P. and Sheffield, S., The GFF and CLE(4). Slides of 2011 talks and private communications.Google Scholar
Miller, J. P. and Sheffield, S., Imaginary Geometry I. Interacting SLEs, Probab. Theory Related Fields 164 (2016), 553–705.Google Scholar
Miller, J. P. and Sheffield, S., Imaginary Geometry II. Reversibility of SLE𝜅(𝜌1; 𝜌2) for 𝜅 ∈ (0, 4), Ann. Probab. 44 (2016), 1647–1722.Google Scholar
Miller, J. P. and Sheffield, S., Imaginary Geometry III. Reversibility of SLE𝜅 for 𝜅 ∈ (4, 8), Ann. Math. 184 (2016), 455–486.Google Scholar
Miller, J. P. and Sheffield, S., Imaginary Geometry IV: Interior rays, whole-plane reversibility, and space-filling trees, Probab. Theory Related Fields (to appear).Google Scholar
Miller, J. P., Sheffield, S. and Werner, W., CLE percolations, preprint, 2016, arXiv:1602.03884.Google Scholar
Nacu, Ş. and Werner, W., Random soups, carpets and fractal dimensions, J. Lond. Math. Soc. (2) 83 (2011), 789–809.Google Scholar
Port, S. C. and Stone, C. J., Brownian Motion and Classical Potential Theory (Academic Press, New York, 1978).Google Scholar
Powell, E. and Wu, H., Level lines of the Gaussian Free Field with general boundary data, Ann. Inst. Henri Poincaré (to appear).Google Scholar
Qian, W. and Werner, W., Coupling the Gaussian free fields with free and with zero boundary conditions via common level lines, preprint, 2017, arXiv:1703.04350.Google Scholar
Rozanov, Yu. A., Markov Random Fields (Springer, New York, 1982).Google Scholar
Schramm, O., Scaling limits of loop-erased random walks and uniform spanning trees, Israel J. Math. 118 (2000), 221–288.Google Scholar
Schramm, O. and Sheffield, S., Contour lines of the discrete two-dimensional Gaussian free field, Acta Math. 202 (2009), 21–137.Google Scholar
Schramm, O. and Sheffield, S., A contour line of the continuum Gaussian free field, Probab. Theory Related Fields 157 (2013), 47–80.Google Scholar
Schramm, O., Sheffield, S. and Wilson, D. B., Conformal radii for conformal loop ensembles, Commun. Math. Phys. 288 (2009), 43–53.Google Scholar
Sepúlveda, A., On thin local sets of the Gaussian free field, preprint, 2017, arXiv:1702.03164.Google Scholar
Sheffield, S., Exploration trees and conformal loop ensembles, Duke Math. J. 147 (2009), 79–129.Google Scholar
Sheffield, S., Conformal weldings of random surfaces: SLE and the quantum gravity zipper, Ann. Probab. 44 (2016), 3474–3545.Google Scholar
Sheffield, S. and Werner, W., Conformal Loop Ensembles: the Markovian characterization and the loop-soup construction, Ann. Math. 176 (2012), 1827–1917.Google Scholar
Werner, W., Some recent aspects of random conformally invariant systems, Ecole d’été de physique des Houches LXXXIII (2006), 57–99.Google Scholar
Werner, W., Topics on the GFF and CLE(4). Lecture Notes, 2016.Google Scholar
Werner, W. and Wu, H., On conformally invariant CLE explorations, Commun. Math. Phys. 320 (2013), 637–661.Google Scholar