Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-27T05:13:17.063Z Has data issue: false hasContentIssue false
  • English
  • Français

The low Mach number limit for the isentropic Euler system with axisymmetric initial data

Published online by Cambridge University Press:  24 May 2012

Taoufik Hmidi
Taoufik Hmidi*
Affiliation:
IRMAR, Université de Rennes 1, Campus de Beaulieu, 35 042 Rennes CEDEX, France (thmidi@univ-rennes1.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is devoted to the study of the low Mach number limit for the isentropic Euler system with axisymmetric initial data without swirl. In the first part of the paper we analyze the problem corresponding to the subcritical regularities, that is 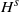${H}^{s} $ with $s\gt \frac{5}{2} $. Taking advantage of the Strichartz estimates and using the special structure of the vorticity we show that the lifespan 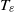${T}_{\varepsilon } $ of the solutions is bounded below by 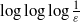$\log \log \log \frac{1}{\varepsilon } $, where $\varepsilon $ denotes the Mach number. Moreover, we prove that the incompressible parts converge to the solution of the incompressible Euler system when the parameter $\varepsilon $ goes to zero. In the second part of the paper we address the same problem but for the Besov critical regularity 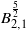${ B}_{2, 1}^{\frac{5}{2} } $. This case turns out to be more subtle because of at least two features. The first one is related to the Beale–Kato–Majda criterion which is not known to be valid for rough regularities. The second one concerns the critical aspect of the Strichartz estimate 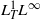${ L}_{T}^{1} {L}^{\infty } $ for the acoustic parts 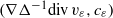$(\nabla {\Delta }^{- 1} \mathrm{div} \hspace{0.167em} {v}_{\varepsilon } , {c}_{\varepsilon } )$: it scales in the space variables like the space of the initial data.

Keywords

incompressible limitaxisymmetrix flowscritical Besov spaces
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 12 , Issue 2 , April 2013 , pp. 335 - 389
Copyright
©Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abidi, H., Hmidi, T. and Keraani, S., On the global well-posedness for the axisymmetric Euler equations, Math. Ann. 347 (1) (2010), 15–41.Google Scholar
Abidi, H., Hmidi, T. and Keraani, S., On the global regularity of axisymmetric Navier–Stokes–Boussinesq system, Discrete Contin. Dyn. Syst. 29 (3) (2011), 737–756.CrossRefGoogle Scholar
Alazard, T., Incompressible limit of the nonisentropic Euler equations with the solid wall boundary conditions, Adv. Differential Equations 10 (1) (2005), 19–44.Google Scholar
Alinhac, S., Temps de vie des solutions régulières des équations d’Euler compressibles axisymétriques en dimension deux, Invent. Math. 111 (3) (1993), 627–670.CrossRefGoogle Scholar
Asano, K., On the incompressible limit of the compressible Euler equation, Japan J. Appl. Math. 4 (3) (1987), 455–488.Google Scholar
Bahouri, H., Chemin, J. Y. and Danchin, R., Fourier analysis and nonlinear partial differential equations, Grundlehren der Mathematischen Wissenschaften, Volume 343. p. xvi+523 pp (Springer, Heidelberg, 2011).Google Scholar
Beale, J. T., Kato, T. and Majda, A., Remarks on the breakdown of smooth solutions for the 3D Euler equations, Comm. Math. Phys. 94 (1984), 61–66.Google Scholar
Bergh, J. and Löfström, J., Interpolation spaces. An introduction. (Springer-Verlag, 1976).Google Scholar
Bony, J.-M., Calcul symbolique et propagation des singularités pour les équations aux dérivées partielles non linéaires, Ann. de l’Éc. Norm. Supér. 14 (1981), 209–246.Google Scholar
Chemin, J.-Y., Perfect incompressible fluids, Oxford Lecture Series in Mathematics and its Applications, Volume 14. (The Clarendon Press Oxford University Press, New York, 1998), Translated from the 1995 French original by Isabelle Gallagher and Dragos Iftimie.Google Scholar
Chen, Q., Miao, C. and Zhang, Z., Well-posedness in critical spaces for the compressible Navier–Stokes equations with density dependent viscosities, Rev. Mat. Iberoam. 26 (3) (2010), 915–946.CrossRefGoogle Scholar
Danchin, R., Zero Mach number limit in critical spaces for compressible Navier–Stokes equations, Ann. Sc. Éc. Norm. Supér. (4) 35 (1) (2002), 27–75.CrossRefGoogle Scholar
Desjardins, B. and Grenier, E., Low Mach number limit of viscous compressible flows in the whole space, R. Soc. Lond. Proc. Ser. A Math. Phys. Eng. Sci. 455 (1986) (1999), 2271–2279.Google Scholar
Desjardins, B., Grenier, E., Lions, P.-L. and Masmoudi, N., Incompressible limit for solutions of the isentropic Navier–Stokes equations with Dirichlet boundary conditions, J. Math. Pures Appl. (9) 78 (5) (1999), 461–471.Google Scholar
Dutrifoy, A. and Hmidi, T., The incompressible limit of solutions of the two-dimensional compressible Euler system with degenerating initial data, Comm. Pure Appl. Math. 57 (9) (2004), 1159–1177.CrossRefGoogle Scholar
Gallagher, I., Résultats récents sur la limite incompressible. Séminaire Bourbaki. Volume 2003/2004. Astérisque No. 299 (2005), Exp. No. 926, vii, 29–57.Google Scholar
Ginibre, J. and Velo, G., Generalized Strichartz inequalities for the wave equation, J. Funct. Anal. 133 (1) (1995), 50–68.Google Scholar
Grassin, M., Global smooth solutions to Euler equations for a perfect gas, Indiana Univ. Math. J. 47 (4) (1998), 1397–1432.Google Scholar
Hmidi, T. and Rousset, F., Global well-posedness for the Euler–Boussinesq system with axisymmetric data, J. Funct. Anal. 260 (3) (2011), 745–796.Google Scholar
Klainerman, S. and Majda, A., Singular limits of quasilinear hyperbolic systems with large parameters and the incompressible limit of compressible fluids, Comm. Pure Appl. Math. 34 (4) (1981), 481–524.CrossRefGoogle Scholar
Klainerman, S. and Majda, A., Compressible and incompressible fluids, Comm. Pure Appl. Math. 35 (5) (1982), 629–651.Google Scholar
Ladyzhenskaya, O. A., Unique solvability in large of a three-dimensional Cauchy problem for the Navier–Stokes equations in the presence of axial symmetry, Zap. Nauchn. Sem. LOMI 7 (1968), 155–177.Google Scholar
Lin, C.-K., On the incompressible limit of the slightly compressible viscous fluid flows, in Nonlinear waves (Sapporo, 1995), GAKUTO Internat. Ser. Math. Sci. Appl., Volume 10. pp. 277–282. (Gakkōtosho, Tokyo, 1997).Google Scholar
Lions, P.-L. and Masmoudi, N., Incompressible limit for a viscous compressible fluid, J. Math. Pures Appl. (9) 77 (6) (1998), 585–627.Google Scholar
Majda, A., Compressible fluid flow and systems of conservation laws in several space variables, Applied Mathematical Sciences, Volume 53. (Springer-Verlag, New York, 1984).Google Scholar
Métivier, G. and Schochet, S., The incompressible limit of the non-isentropic Euler equations, Arch. Ration. Mech. Anal. 158 (1) (2001), 61–90.Google Scholar
Rammaha, M. A., Formation of singularities in compressible fluids in two-space dimensions, Proc. Amer. Math. Soc. 107 (3) (1989), 705–714.Google Scholar
Shirota, T. and Yanagisawa, T., Note on global existence for axially symmetric solutions of the Euler system, Proc. Japan Acad. Ser. A Math. Sci. 70 (10) (1994), 299–304.Google Scholar
Serre, D., Solutions classiques globales des équations d’Euler pour un fluide parfait compressible, Ann. Inst. Fourier (Grenoble) 47 (1) (1997), 139–153.Google Scholar
Sideris, Thomas C., Formation of singularities in three-dimensional compressible fluids, Comm. Math. Phys. 101 (4) (1985), 475–485.Google Scholar
Triebel, H., Theory of function spaces, Monographs in Mathematics, Volume 78. (Birkhäuser Verlag, Basel, 1983).Google Scholar
Ukhovskii, M. R. and Yudovich, V. I., Axially symmetric flows of ideal and viscous fluids filling the whole space, Prikl. Mat. Mekh. 32 (1) (1968), 59–69.Google Scholar
Ukai, S., The incompressible limit and the initial layer of the compressible Euler equation, J. Math. Kyoto Univ. 26 (2) (1086), 323–331.Google Scholar