Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-24T08:56:34.781Z Has data issue: false hasContentIssue false
  • English
  • Français

IRREGULAR HODGE FILTRATION OF SOME CONFLUENT HYPERGEOMETRIC SYSTEMS

Part of: Analytic spaces (Co)homology theory

Published online by Cambridge University Press:  24 May 2019

Alberto Castaño Domínguez Open the ORCID record for Alberto Castaño Domínguez [Opens in a new window]  and
Christian Sevenheck
Alberto Castaño Domínguez
Affiliation:
Instituto de Matemáticas, Universidade de Santiago de Compostela, 15782Santiago de Compostela, Spain (alberto.castano@usc.es)
Christian Sevenheck
Affiliation:
Fakultät für Mathematik, Technische Universität Chemnitz, 09107Chemnitz, Germany (christian.sevenheck@mathematik.tu-chemnitz.de)
Get access Rights & Permissions [Opens in a new window]

Abstract

We determine the irregular Hodge filtration, as introduced by Sabbah, for the purely irregular hypergeometric 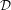${\mathcal{D}}$-modules. We obtain, in particular, a formula for the irregular Hodge numbers of these systems. We use the reduction of hypergeometric systems from GKZ-systems as well as comparison results to Gauss–Manin systems of Laurent polynomials via Fourier–Laplace and Radon transformations.

Keywords

D-modulesirregular Hodge filtrationhypergeometric systemstwistor D-modules

MSC classification

Primary: 14F10: Differentials and other special sheaves; D-modules; Bernstein-Sato ideals and polynomials 32C38: Sheaves of differential operators and their modules, $D$-modules
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 2 , March 2021 , pp. 627 - 668
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors are partially supported by the project SISYPH: ANR-13-IS01-0001-01/02 and DFG grant SE 1114/5-1.

References

Adolphson, A., Hypergeometric functions and rings generated by monomials, Duke Math. J. 73(2) (1994), 269–290.10.1215/S0012-7094-94-07313-4CrossRefGoogle Scholar
Arinkin, D., Rigid irregular connections on ℙ1, Compos. Math. 146(5) (2010), 1323–1338.CrossRefGoogle Scholar
Borisov, L. A. and Horja, R. P., Mellin-Barnes integrals as Fourier–Mukai transforms, Adv. Math. 207(2) (2006), 876–927.CrossRefGoogle Scholar
Berkesch, C., Matusevich, L. F. and Walther, U., On normalized Horn systems, preprint, 2018, arXiv:1806.03355 [math.AG].Google Scholar
Brieskorn, E., Die Monodromie der isolierten Singularitäten von Hyperflächen, Manuscripta Math. 2 (1970), 103–161.CrossRefGoogle Scholar
Domínguez, A. Castaño, Reichelt, T. and Sevenheck, C., Examples of hypergeometric twistor ${\mathcal{D}}$-modules, Algebra Number Theory, preprint, 2018,arXiv:1803.04886 [math.AG], to appear.CrossRefGoogle Scholar
Corti, A. and Golyshev, V., Hypergeometric equations and weighted projective spaces, Sci. China Math. 54(8) (2011), 1577–1590.CrossRefGoogle Scholar
Cox, D. A. and Katz, S., Mirror Symmetry and Algebraic Geometry, Mathematical Surveys and Monographs, Volume 68 (American Mathematical Society, Providence, RI, 1999).CrossRefGoogle Scholar
D’Agnolo, A. and Eastwood, M., Radon and Fourier transforms for 𝓓-modules, Adv. Math. 180(2) (2003), 452–485.10.1016/S0001-8708(03)00011-2CrossRefGoogle Scholar
Dimca, A., Sheaves in topology, in Universitext (Springer, Berlin, 2004).Google Scholar
Denef, J. and Loeser, F., Weights of exponential sums, intersection cohomology, and Newton polyhedra, Invent. Math. 106(2) (1991), 275–294.CrossRefGoogle Scholar
Douai, A. and Sabbah, C., Gauss–Manin systems, Brieskorn lattices and Frobenius structures. I, Ann. Inst. Fourier (Grenoble) 53(4) (2003), 1055–1116.CrossRefGoogle Scholar
Douai, A. and Sabbah, C., Gauss–Manin systems, Brieskorn lattices and Frobenius structures. II, Frobenius manifolds, Aspects of Mathematics, Volume E36, pp. 1–18 (Vieweg, Wiesbaden, 2004).Google Scholar
Dettweiler, M. and Sabbah, C., Hodge theory of the middle convolution, Publ. Res. Inst. Math. Sci. 49(4) (2013), 761–800.CrossRefGoogle Scholar
Esnault, H., Sabbah, C. and Yu, J.-D., E 1 -degeneration of the irregular Hodge filtration, J. Reine Angew. Math. 729 (2017), 171–227.Google Scholar
Fedorov, R., Variations of Hodge structures for hypergeometric differential operators and parabolic Higgs bundles, Int. Math. Res. Not. IMRN 18 (2018), 5583–5608.CrossRefGoogle Scholar
Gel’fand, I. M., Kapranov, M. M. and Zelevinsky, A. V., Discriminants, resultants, and multidimensional determinants, in Mathematics: Theory & Applications (Birkhäuser Boston Inc, Boston, MA, 1994).Google Scholar
de Gregorio, I., Mond, D. and Sevenheck, C., Linear free divisors and Frobenius manifolds, Compos. Math. 145(5) (2009), 1305–1350.CrossRefGoogle Scholar
Hertling, C. and Sevenheck, C., Nilpotent orbits of a generalization of Hodge structures, J. Reine Angew. Math. 609 (2007), 23–80.Google Scholar
Hotta, R., Takeuchi, K. and Tanisaki, T., 𝓓-Modules, Perverse Sheaves, and Representation Theory, Progress in Mathematics, Volume 236 (Birkhä user Boston Inc, Boston, MA, 2008). Translated from the 1995 Japanese edition by Takeuchi.CrossRefGoogle Scholar
Katz, N. M., Exponential Sums and Differential Equations, Annals of Mathematics Studies, Volume 124 (Princeton University Press, Princeton, NJ, 1990).CrossRefGoogle Scholar
Katzarkov, L., Kontsevich, M. and Pantev, T., Bogomolov–Tian–Todorov theorems for Landau–Ginzburg models, J. Differential Geom. 105(1) (2017), 55–117.CrossRefGoogle Scholar
Kouchnirenko, A. G., Polyèdres de Newton et nombres de Milnor, Invent. Math. 32(1) (1976), 1–31.CrossRefGoogle Scholar
Martin, N., Middle multiplicative convolution and hypergeometric equations, preprint, 2018, arXiv:1809.08867 [math.AG].Google Scholar
Mochizuki, T., Wild harmonic bundles and wild pure twistor D-modules, Astérisque (340) (2011), x+607.Google Scholar
Mochizuki, T., Mixed twistor 𝓓-modules, Lecture Notes in Mathematics, Volume 2125 (Springer, Cham, 2015).CrossRefGoogle Scholar
Mochizuki, T., Twistor property of GKZ-hypergeometric systems, preprint, 2015, arXiv:1501.04146 [math.AG].Google Scholar
Reichelt, T., Laurent polynomials, GKZ-hypergeometric systems and mixed Hodge modules, Compos. Math. 150 (2014), 911–941.CrossRefGoogle Scholar
Reichelt, T. and Sevenheck, C., Hypergeometric Hodge modules, Algebraic Geom., preprint, 2015, arXiv:1503.01004 [math.AG] 2015, to appear.Google Scholar
Reichelt, T. and Sevenheck, C., Logarithmic Frobenius manifolds, hypergeometric systems and quantum 𝓓-modules, J. Algebraic Geom. 24(2) (2015), 201–281.CrossRefGoogle Scholar
Reichelt, T. and Sevenheck, C., Non-affine Landau-Ginzburg models and intersection cohomology, Ann. Sci. Éc. Norm. Supér. 50(3) (2017), 665–753.CrossRefGoogle Scholar
Sabbah, C., Déformations isomonodromiques et variétés de Frobenius, in Savoirs Actuels (EDP Sciences, Les Ulis, 2002). Mathématiques.Google Scholar
Sabbah, C., Hypergeometric periods for a tame polynomial, Port. Math. (NS) 63(2) (2006), 173–226.Google Scholar
Sabbah, C., Fourier–Laplace transform of a variation of polarized complex Hodge structure, J. Reine Angew. Math. 621 (2008), 123–158.Google Scholar
Sabbah, C., Irregular Hodge theory (with the collaboration of Jeng-Daw Yu), Mém. Soc. Math. Fr. (NS) (156) (2018), vi+126.Google Scholar
Sabbah, C., Some properties and applications of Brieskorn lattices, J. Singul. 18 (2018), 239–248.Google Scholar
Saito, M., Modules de Hodge polarisables, Publ. Res. Inst. Math. Sci. 24(6) (1988), 849–995. 1989.CrossRefGoogle Scholar
Saito, M., Mixed Hodge modules, Publ. Res. Inst. Math. Sci. 26(2) (1990), 221–333.CrossRefGoogle Scholar
Schmid, W., Variation of Hodge structure: the singularities of the period mapping, Invent. Math. 22 (1973), 211–319.CrossRefGoogle Scholar
Shamoto, Y., Hodge–Tate conditions for Landau–Ginzburg models, Publ. Res. Inst. Math. Sci. 54(3) (2018), 469–515.CrossRefGoogle Scholar
Simpson, C. T., Harmonic bundles on noncompact curves, J. Amer. Math. Soc. 3(3) (1990), 713–770.CrossRefGoogle Scholar
Sabbah, C. and Yu, J.-D., On the irregular Hodge filtration of exponentially twisted mixed Hodge modules, Forum Math. Sigma 3(e9) (2015), 71 pp.CrossRefGoogle Scholar
Sabbah, C. and Yu, J.-D., Irregular Hodge numbers of confluent hypergeometric differential equations, preprint, 2018, arXiv:1812.00755 [math.AG], 2018.Google Scholar
Jeng-Daw, Y., Irregular Hodge filtration on twisted de Rham cohomology, Manuscripta Math. 144(1–2) (2014), 99–133.Google Scholar