Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-27T12:26:15.464Z Has data issue: false hasContentIssue false
  • English
  • Français

HIGHER MOMENT FORMULAE AND LIMITING DISTRIBUTIONS OF LATTICE POINTS

Part of: Multiplicative number theory Noncompact transformation groups

Published online by Cambridge University Press:  28 November 2023

Mahbub Alam ,
Anish Ghosh  and
Jiyoung Han Open the ORCID record for Jiyoung Han [Opens in a new window]
Mahbub Alam
Affiliation:
Department of Mathematics, Uppsala University, Sweden https://sites.google.com/view/mahbubweb (mahbub.dta@gmail.com; mahbub.alam@math.uu.se)
Anish Ghosh
Affiliation:
School of Mathematics, Tata Institute of Fundamental Research, Homi Bhabha Road, Colaba, Mumbai, India 400005 (ghosh@math.tifr.res.in)
Jiyoung Han*
Affiliation:
Korea Institute for Advanced Study (KIAS), Seoul, Republic of Korea
*
hanjiwind@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish higher moment formulae for Siegel transforms on the space of affine unimodular lattices as well as on certain congruence quotients of 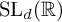$\mathrm {SL}_d({\mathbb {R}})$. As applications, we prove functional central limit theorems for lattice point counting for affine and congruence lattices using the method of moments.

Keywords

Lattice point countingGeometry of numbersBrownian motionCentral Limit TheoremSiegel transformHigher moments

MSC classification

Primary: 11N45: Asymptotic results on counting functions for algebraic and topological structures
Secondary: 22F30: Homogeneous spaces
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , First View , pp. 1 - 45
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M., Ghosh, A. and Yu, S., Quantitative Diophantine approximation with congruence conditions, J. Théor. Nombres Bordeaux 33(1) (2021), 261–271.CrossRefGoogle Scholar
Athreya, J. S., Random affine lattices, Contemp. Math. 639 (2015), 160–74.CrossRefGoogle Scholar
Billingsley, P., Convergence of Probability Measures (Wiley Series in Probability and Statistics), second edn. (John Wiley & Sons Inc., New York, 1999).CrossRefGoogle Scholar
El-Baz, D., Marklof, J. and Vinogradov, I., The distribution of directions in an affine lattice: Two-point correlations and mixed moments, Int. Math. Res. Not. IMRN 2015(5) (2015), 1371–1400.Google Scholar
Ghosh, A. and Han, J., Values of inhomogeneous forms at S-integral points, Mathematika 68(2) (2022), 565–593.CrossRefGoogle Scholar
Ghosh, A., Kelmer, D. and Yu, S., Effective density for inhomogeneous quadratic forms I: Generic forms and fixed shifts, Int. Math. Res. Not. IMRN 2022(6) (2022), 4682–4719.CrossRefGoogle Scholar
Han, J., Lim, S. and Mallahi-Karai, K., Asymptotic distribution of values of isotropic quadratic forms at $S$ -integral points, J. Mod. Dyn. 11 (2017), 501–550.CrossRefGoogle Scholar
Han, J., Rogers’ mean value theorem for S-arithmetic Siegel transform and applications to the geometry of numbers, J. Number Theory 240 (2022), 74–106.CrossRefGoogle Scholar
Kim, S., Random lattice vectors in a set of size O(n), Int. Math. Res. Not. IMRN 2020(5) (2020), 1385–1416.CrossRefGoogle Scholar
Marklof, J., The n-point correlations between values of a linear form, Ergodic Theory Dynam. Systems 20 (2000), 1127–1172.CrossRefGoogle Scholar
Marklof, J. and Strömbergsson, A., The distribution of free path lengths in the periodic Lorentz gas and related lattice point problems, Ann. of Math. (2) 172(3) (2010), 1949–2033.CrossRefGoogle Scholar
Prasad, G., Volumes of S-arithmetic quotients of semi-simple groups, Inst. Hautes Études Sci. Publ. Math. 69 (1989), 91–117. With an appendix by Moshe Jarden and the author.CrossRefGoogle Scholar
Rogers, C., Mean values over the space of lattices, Acta Math. 94 (1955), 249–287.CrossRefGoogle Scholar
Rogers, C., The moments of the number of points of a lattice in a bounded set, Phil. Trans. Roy. Soc. London. Ser. A. 248 (1955), 225–251.Google Scholar
Rogers, C., Two integral inequalities, J. London Math. Soc. 31 (1956), 235–238.CrossRefGoogle Scholar
Rogers, C., The number of lattice points in a set, Proc. London Math. Soc. (3) 6 (1956), 305–320.CrossRefGoogle Scholar
Schmidt, W. M., On the convergence of mean values over lattices, Canad. J. Math. 10 (1958), 103–110.CrossRefGoogle Scholar
Schmidt, W. M., Masstheorie in der Geometrie der Zahlen, Acta Math. 102 (1959), 159–224.CrossRefGoogle Scholar
Schmidt, W. M., ‘A metrical theorem in geometry of numbers’, Trans. Amer. Math. Soc. 95 (1960), 516–529.CrossRefGoogle Scholar
Siegel, C., A mean value theorem in geometry of numbers, Ann. Math. 46 (1945), 340–347.CrossRefGoogle Scholar
Siegel, C., Lectures on the Geometry of Numbers (Springer-Verlag Berlin Heidelberg GmbH, 1989). x+160 pp.CrossRefGoogle Scholar
Strömbergsson, A. and Södergren, A., On the generalized circle problem for a random lattice in large dimension, Adv. Math. 345 (2019), 1042–1074.CrossRefGoogle Scholar
Södergren, A., On the Poisson distribution of lengths of lattice vectors in a random lattice, Math. Z. 269(3–4) (2011), 945–954.CrossRefGoogle Scholar