Article contents
THE DYNAMICAL MORDELL–LANG CONJECTURE FOR ENDOMORPHISMS OF SEMIABELIAN VARIETIES DEFINED OVER FIELDS OF POSITIVE CHARACTERISTIC
Published online by Cambridge University Press: 24 June 2019
Abstract
Let 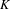 $K$ be an algebraically closed field of prime characteristic
$K$ be an algebraically closed field of prime characteristic 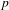 $p$, let
$p$, let 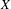 $X$ be a semiabelian variety defined over a finite subfield of
$X$ be a semiabelian variety defined over a finite subfield of 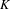 $K$, let
$K$, let 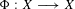 $\unicode[STIX]{x1D6F7}:X\longrightarrow X$ be a regular self-map defined over
$\unicode[STIX]{x1D6F7}:X\longrightarrow X$ be a regular self-map defined over 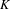 $K$, let
$K$, let 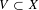 $V\subset X$ be a subvariety defined over
$V\subset X$ be a subvariety defined over 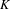 $K$, and let
$K$, and let 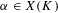 $\unicode[STIX]{x1D6FC}\in X(K)$. The dynamical Mordell–Lang conjecture in characteristic
$\unicode[STIX]{x1D6FC}\in X(K)$. The dynamical Mordell–Lang conjecture in characteristic 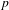 $p$ predicts that the set
$p$ predicts that the set 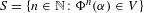 $S=\{n\in \mathbb{N}:\unicode[STIX]{x1D6F7}^{n}(\unicode[STIX]{x1D6FC})\in V\}$ is a union of finitely many arithmetic progressions, along with finitely many
$S=\{n\in \mathbb{N}:\unicode[STIX]{x1D6F7}^{n}(\unicode[STIX]{x1D6FC})\in V\}$ is a union of finitely many arithmetic progressions, along with finitely many 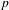 $p$-sets, which are sets of the form
$p$-sets, which are sets of the form 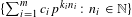 $\{\sum _{i=1}^{m}c_{i}p^{k_{i}n_{i}}:n_{i}\in \mathbb{N}\}$ for some
$\{\sum _{i=1}^{m}c_{i}p^{k_{i}n_{i}}:n_{i}\in \mathbb{N}\}$ for some 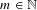 $m\in \mathbb{N}$, some rational numbers
$m\in \mathbb{N}$, some rational numbers  $c_{i}$ and some non-negative integers
$c_{i}$ and some non-negative integers 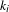 $k_{i}$. We prove that this conjecture is equivalent with some difficult diophantine problem in characteristic 0. In the case
$k_{i}$. We prove that this conjecture is equivalent with some difficult diophantine problem in characteristic 0. In the case 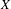 $X$ is an algebraic torus, we can prove the conjecture in two cases: either when
$X$ is an algebraic torus, we can prove the conjecture in two cases: either when 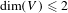 $\dim (V)\leqslant 2$, or when no iterate of
$\dim (V)\leqslant 2$, or when no iterate of 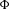 $\unicode[STIX]{x1D6F7}$ is a group endomorphism which induces the action of a power of the Frobenius on a positive dimensional algebraic subgroup of
$\unicode[STIX]{x1D6F7}$ is a group endomorphism which induces the action of a power of the Frobenius on a positive dimensional algebraic subgroup of 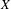 $X$. We end by proving that Vojta’s conjecture implies the dynamical Mordell–Lang conjecture for tori with no restriction.
$X$. We end by proving that Vojta’s conjecture implies the dynamical Mordell–Lang conjecture for tori with no restriction.
Keywords
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 2 , March 2021 , pp. 669 - 698
- Copyright
- © Cambridge University Press 2019
Footnotes
The second author has been partially supported by a discovery grant from the National Science and Engineering Board of Canada. The third author has been partially supported by grant DMS-1363372 of the United States National Science Foundation and a Simons Foundation Fellowship.
References
- 6
- Cited by





