Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-04-30T11:38:46.441Z Has data issue: false hasContentIssue false
  • English
  • Français

ON MORPHISMS KILLING WEIGHTS AND STABLE HUREWICZ-TYPE THEOREMS

Part of: Cycles and subschemes Homology and cohomology theories Abelian categories Homotopy theory

Published online by Cambridge University Press:  24 October 2022

Mikhail V. Bondarko Open the ORCID record for Mikhail V. Bondarko [Opens in a new window]
Mikhail V. Bondarko*
Affiliation:
St. Petersburg State University, 7/9 Universitetskaya nab., St. Petersburg, 199034 Russia; St. Petersburg Department of Steklov Math. Institute, Fontanka 27, St. Petersburg, 191023, Russia
*
m.bondarko@spbu.ru
Get access Rights & Permissions [Opens in a new window]

Abstract

For a weight structure w on a triangulated category 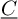$\underline {C}$ we prove that the corresponding weight complex functor and some other (weight-exact) functors are ‘conservative up to weight-degenerate objects’; this improves earlier conservativity formulations. In the case 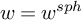$w=w^{sph}$ (the spherical weight structure on 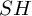$SH$), we deduce the following converse to the stable Hurewicz theorem: 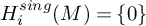$H^{sing}_{i}(M)=\{0\}$ for all 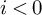$i<0$ if and only if 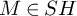$M\in SH$ is an extension of a connective spectrum by an acyclic one. We also prove an equivariant version of this statement.

The main idea is to study M that has no weights $m,\dots ,n$ (‘in the middle’). For 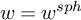$w=w^{sph}$, this is the case if there exists a distinguished triangle 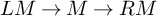$LM\to M\to RM$, where 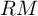$RM$ is an n-connected spectrum and 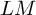$LM$ is an 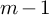$m-1$-skeleton (of M) in the sense of Margolis’s definition; this happens whenever 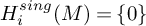$H^{sing}_i(M)=\{0\}$ for 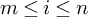$m\le i\le n$ and 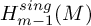$H^{sing}_{m-1}(M)$ is a free abelian group. We also consider morphisms that kill weights $m,\dots ,n$; those ‘send n-w-skeleta into 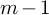$m-1$-w-skeleta’.

MSC classification

Primary: 55P42: Stable homotopy theory, spectra 55N91: Equivariant homology and cohomology
Secondary: 14C15: (Equivariant) Chow groups and rings; motives 55P91: Equivariant homotopy theory 18E40: Torsion theories, radicals
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 23 , Issue 2 , March 2024 , pp. 521 - 556
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balmer, P. and Schlichting, M., ‘Idempotent completion of triangulated categories’, J. of Algebra 236(2) (2001), 819–834.CrossRefGoogle Scholar
Beilinson, A., Bernstein, J. and Deligne, P., ‘Faisceaux pervers’, Asterisque 100, (1982), 5–171.Google Scholar
Beilinson, A. and Vologodsky, V., ‘A DG guide to Voevodsky motives’, Geom. Funct. Analysis 17(6) (2008), 1709–1787.CrossRefGoogle Scholar
Bondarko, M. V., ‘Weight structures vs. $t$ -structures; weight filtrations, spectral sequences, and complexes (for motives and in general)’, J. of K-theory 6(3) (2010), 387–504, see also http://arxiv.org/abs/0704.4003 CrossRefGoogle Scholar
Bondarko, M. V., ‘Intersecting the dimension and slice filtrations for motives’, Homology, Homotopy and Appl. 20(1) (2018), 259–274.CrossRefGoogle Scholar
Bondarko, M. V., ‘On morphisms killing weights and Hurewicz-type theorems’, Preprint, 2019, arxiv.org/abs/1904.12853.Google Scholar
Bondarko, M. V., ‘On weight complexes, pure functors, and detecting weights’, J. of Algebra 574 (2021), 617–668.CrossRefGoogle Scholar
Bondarko, M. V. and Kumallagov, D. Z., ‘On Chow-weight homology of motivic complexes and its relation to motivic homology (Russian)’, Vestnik St. Petersburg University, Mathematics 65(4) (2020), 560–587. Translation in Vestnik St. Peters. Univers., Mathematics 53(4) (2020), 377–397.CrossRefGoogle Scholar
Bondarko, M. V. and Sosnilo, V. A., ‘On constructing weight structures and extending them to idempotent extensions’, Homology, Homotopy and Appl. 20(1) (2018), 37–57.CrossRefGoogle Scholar
Bondarko, M. V. and Sosnilo, V. A., ‘On purely generated $\alpha$ -smashing weight structures and weight-exact localizations’, J. of Algebra 535 (2019), 407–455.CrossRefGoogle Scholar
Bondarko, M. V. and Sosnilo, V. A., ‘On Chow-weight homology of geometric motives’, Trans. AMS. 375(1) (2022), 173–244. See also arxiv.org/abs/1411.6354.CrossRefGoogle Scholar
Bondarko, M. V. and Vostokov, S. V., ‘Killing weights from the perspective of $t$ -structures’, to appear in Proc. Steklov Inst. Math. Google Scholar
Déglise, F., ‘Modules homotopiques (homotopy modules)’, Doc. Math. 16 (2011), 411–455.CrossRefGoogle Scholar
Greenlees, J. P. C., ‘Some remarks on projective Mackey functors’, J. of Pure and Appl. Algebra 81(1) (1992), 17–38.CrossRefGoogle Scholar
Hovey, M., Palmieri, J. and Strickland, N., ‘Axiomatic stable homotopy theory’, American Mathematical Society (1997), 114.Google Scholar
Keller, B., ‘On differential graded categories’, in International Congress of Mathematicians, vol. II, (Eur. Math. Soc., Zürich, 2006), 151–190.Google Scholar
Kelly, S., ‘ Triangulated categories of motives in positive characteristic,’ Ph.D. thesis, Université Paris 13 and the Australian National University, 2012, arxiv.org/abs/1305.5349.Google Scholar
Lewis, L. G. Jr., ‘The equivariant Hurewicz map’, Trans. of the American Math. Soc. 329(2) (1992), 433–472.CrossRefGoogle Scholar
Lewis, L. G. Jr., May, J. P., Steinberger, M. and McClure, J. E., ‘Equivariant stable homotopy theory’, Lecture Notes in Mathematics 1213 (1986), x+538.Google Scholar
Margolis, H. R., Spectra and the Steenrod Algebra: Modules over the Steenrod Algebra and the Stable Homotopy Category (Elsevier, North-Holland, Amsterdam-New York, 1983).Google Scholar
May, J. P., Equivariant Homotopy and Cohomology Theory, with contributions by M. Cole, G. Comezana, S. Costenoble, A. D. Elmendorf, J. P. C. Greenlees, L. G. Lewis, Jr., R. J. Piacenza, G. Triantafillou, and S. Waner, CBMS Regional Conference Series in Mathematics , 91 (American Math. Soc., Providence, 1996).Google Scholar
Modoi, G. C., ‘Reasonable triangulated categories have filtered enhancements’, Proc . Amer. Math. Soc. 147 (2019), 2761–2773.CrossRefGoogle Scholar
Neeman, A., Triangulated Categories, Annals of Mathematics Studies, 148 (Princeton University Press, Princeton, NJ, 2001), viii+449.CrossRefGoogle Scholar
Pauksztello, D., ‘Compact cochain objects in triangulated categories and co-t-structures’, Central European Journal of Math. 6(1) (2008), 25–42.CrossRefGoogle Scholar
Schnürer, O., ‘Homotopy categories and idempotent completeness, weight structures and weight complex functors’, Preprint, 2011, arxiv.org/abs/1107.1227.Google Scholar
Sosnilo, V. A., ‘Theorem of the heart in negative $K$ -theory for weight structures’, Doc. Math. 24 (2019), 2137–2158.CrossRefGoogle Scholar
Thomason, R. W., ‘The classification of triangulated subcategories’, Comp. Math. 105(1) (1997), 1–27.CrossRefGoogle Scholar
Wildeshaus, J., ‘Chow motives without projectivity’, Comp. Math. 145(5) (2009), 1196–1226.CrossRefGoogle Scholar
Wildeshaus, J., ‘Weights and conservativity’, Algebraic Geometry 5(6) (2018), 686–702.CrossRefGoogle Scholar