Research Article
Isomorphic subgraphs having minimal intersections
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-306
-
- Article
-
- You have access
- Export citation
Corrigendum
2-Groups of almost maximal class: corrigendum
-
- Published online by Cambridge University Press:
- 09 April 2009, p. 307
-
- Article
-
- You have access
- Export citation
Research Article
The endomorphism ring of a locally free module
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 308-326
-
- Article
-
- You have access
- Export citation
Two characterizations of quasi-pseudometrizable bitopological spaces
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 327-333
-
- Article
-
- You have access
- Export citation
A renorming theorem for dual spaces
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 334-337
-
- Article
-
- You have access
- Export citation
A note on linear forms in a class of E-functions and G-functions
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 338-348
-
- Article
-
- You have access
- Export citation
Non-reflexive double triangles
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 349-356
-
- Article
-
- You have access
- Export citation
On maxi-quasiprojective modules
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 357-368
-
- Article
-
- You have access
- Export citation
Central relations on lattices
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 369-372
-
- Article
-
- You have access
- Export citation
Inverse semigroups with idempotents dually well-ordered
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 373-385
-
- Article
-
- You have access
- Export citation
A problem in two-dimensional integration
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 386-404
-
- Article
-
- You have access
- Export citation
The simultaneous representation of integers by products of certain rational functions
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 405-420
-
- Article
-
- You have access
- Export citation
Index
Index
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 421-422
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 35 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 35 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

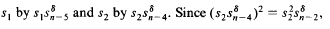 we may suppose δ=0.’
we may suppose δ=0.’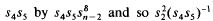 remains unaltered. Thus the case δ=1 is omitted in the paper.
remains unaltered. Thus the case δ=1 is omitted in the paper.