Article contents
Transferring Optimal Dualities: Theory and Practice
Published online by Cambridge University Press: 09 April 2009
Abstract
Consider the quasi-variety 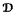 generated by a finite algebra
generated by a finite algebra 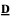 and assume that
and assume that 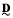 yields a natural duality on
yields a natural duality on 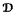 based on
based on 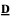 which is optimal modulo endomorphisms. We shoe that, provided
which is optimal modulo endomorphisms. We shoe that, provided 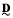 satisfies certain minimality conditions, we can transfer this duality to a natural duality on
satisfies certain minimality conditions, we can transfer this duality to a natural duality on 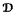 based on
based on 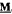 , which is also optimal modulo endormorphisms, for any finite algebra
, which is also optimal modulo endormorphisms, for any finite algebra 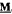 in
in 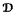 that has a subalgebra isomorphic to
that has a subalgebra isomorphic to 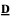 .
.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 2003
References
- 3
- Cited by




